§ 4.4.6. Одноканальная СМО с неограниченной очередью
Пусть имеется одноканальная СМО с очередью.
Предположим, что на очередь не наложено каких-либо ограничений (по длине, по
времени ожидания). На СМО поступает поток заявок с интенсивностью 
; поток обслуживаний имеет интенсивность 
, обратную среднему времени обслуживания заявки 
. Найдем финальные вероятности состояний СМО, а также
характеристики ее эффективности: 
(среднее число заявок
в системе), 
(среднее время
пребывания заявки в очереди), 
(среднее число заявок
в очереди), 
(среднее время
пребывания заявки в очереди), 
(вероятность того что
канал занят).
Абсолютная пропускная способность 
СМО равна
интенсивности потока заявок в силу того, что
очередь не ограничена и все заявки будут обслужены. Откуда относительная
пропускная способность СМО равна единице.
Рис. 28. Граф состояний одноканальной СМО с неограниченной очередью
Состояния системы:
- канал свободен;
- канал занят, очереди
нет;
- канал занят, одна
заявка в очереди;
......
- канал занят, 
заявок в очереди.
......
Схема СМО с неограниченной очередью есть схема гибели
и размножения с бесконечным числом состояний (рисунок 28). Финальные
вероятности для такой СМО существуют только тогда, когда система не перегружена
(
). Если приведенная интенсивность потока заявок больше либо
равна единице (
), при 
очередь неограниченно
растет.
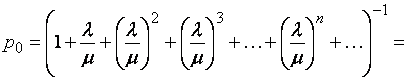
Ряд в формуле представляет собой геометрическую
прогрессию и при сходится.
... 
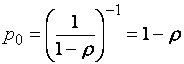
Вероятности образуют геометрическую прогрессию. Самое вероятное состояние – канал свободен.
Найдем среднее число заявок в очереди.
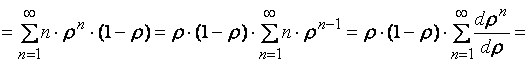
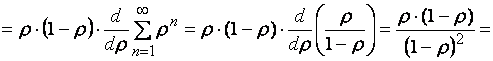
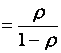
По формуле Литтла:
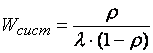
Найдем среднее число заявок в очереди . По правилу сложений математических ожиданий, среднее число
заявок в очереди равно разности среднего числа заявок в системе и их среднего
числа под обслуживанием. Число заявок под обслуживанием может быть либо нулем,
либо единицей. Причем вероятность такой случайной величины равно вероятности
того, что канал занят.
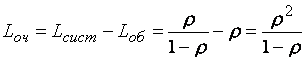
По формуле Литтла:
Назад к разделу "§ 4.4.5. Многоканальная система массового обслуживания с отказами (задача Эрланга)"
Вперед к разделу "§ 4.4.7. Многоканальная СМО с неограниченной очередью"