§ 4.4.5. Многоканальная система массового обслуживания с отказами (задача Эрланга)

 

Потоком обслуживаний называется поток заявок, обслуживаемых одним непрерывно занятым каналом. Имеется  каналов, на которые поступает поток заявок с интенсивностью . Поток обслуживаний имеет интенсивность  (величина, обратная среднему времени обслуживания ). Найдем финальные вероятности, а также характеристики ее эффективности:

 - абсолютная пропускная способность, т.е. среднее число заявок, обслуживаемых в единицу времени;

 - относительная пропускная способность, т.е. средняя доля пришедших заявок, обслуживаемых системой;

 - вероятность отказа, .т.е. вероятность того, что заявка покинет СМО не обслуженной;

 - среднее число занятых каналов.

Состояния системы будем нумеровать по числу заявок, находящихся в системе:

 - в СМО нет ни одной заявки;

 - в СМО находится одна заявка (занят один канал);

.....

 - в СМО находится  заявок (все  каналов заняты).

 

Граф состояний соответствует схеме гибели и размножения. Разметим этот граф – проставим у стрелок интенсивности потоков событий. Из  в  систему переводит поток заявок с интенсивностью . Тот же поток переводит систему из любого левого состояния в соседнее правое.

Проставим интенсивности у нижних стрелок. Пусть система находится в состоянии . Он производит  обслуживаний в единицу времени. Пусть система находится в состоянии . Чтобы ей перейти в , нужно, чтобы закончил обслуживание либо первый канал, либо второй; суммарная интенсивность их потоков обслуживаний равна . Суммарный поток обслуживаний, даваемый  каналами, имеет интенсивность .

Зная все интенсивности, воспользуемся (13) и (14) для финальных вероятностей в схеме гибели и размножения.

                       

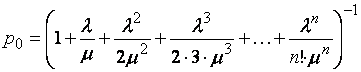
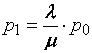
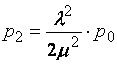
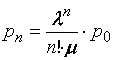
Заменим в формулах 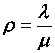 - приведенная интенсивность потока заявок, или среднее число заявок, приходящее за среднее время обслуживания одной заявки. Тогда,

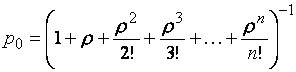                                            (19)

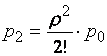
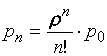                                 (20)

Формулы (19) и (20) для финальных вероятностей состояний называются формулами Эрланга. Вероятность отказа в рассматриваемой СМО равна вероятности того, что все каналы будут заняты: .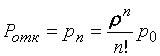

Относительная пропускная способность, равна:

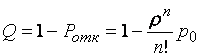
Абсолютная пропускная способность равна:

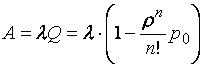
Среднее число занятых каналов  можно найти как математическое ожидание дискретной случайно величины с возможными значениями 0, 1, 2, ... n и вероятностями эти значений :

.

 

 

К оглавлению

Назад к разделу "§ 4.4.4. Формула Литтла"

Вперед к разделу "§ 4.4.6. Одноканальная СМО с неограниченной очередью"