![]() - среднее число заявок, находящееся в системе
массового обслуживания (обслуживаемых или стоящих в очереди).
- среднее число заявок, находящееся в системе
массового обслуживания (обслуживаемых или стоящих в очереди).
![]() - среднее время пребывание заявки в систем.
- среднее время пребывание заявки в систем.
Рассмотрим любую систему массового обслуживания и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность.
Пусть, ![]() - число заявок,
прибывших в СМО до момента
- число заявок,
прибывших в СМО до момента ![]() ;
; ![]() - число заявок,
покинувших СМО до момента
- число заявок,
покинувших СМО до момента ![]() (рисунок 27).
(рисунок 27).
![]()
![]()
![]()
![]()
![]() 0 T t
0 T t
Рис. 27. Число заявок в системе
массового обслуживания в момент времени ![]()
Обе функции являются случайными и меняются скачком в
моменты приходов и уходов заявок. Функция ![]() , - число заявок, находящихся в очереди. Рассмотрим очень
большой промежуток времени
, - число заявок, находящихся в очереди. Рассмотрим очень
большой промежуток времени ![]() и вычислим для него
среднее число заявок, находящихся в СМО:
и вычислим для него
среднее число заявок, находящихся в СМО:
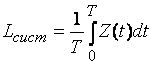 (15)
(15)
Этот интеграл представляет собой площадь фигуры,
заштрихованной на рисунке. Фигура состоит из прямоугольников, каждый из которых
имеет высоту, равную единице, и основание, равное времени пребывания в системе
соответствующей заявки. Обозначим эти времена ![]() . Таким образом, при достаточно больших
. Таким образом, при достаточно больших ![]() , можно считать, что
, можно считать, что
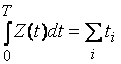 , где сумма распространяется на все заявки, пришедшие за
время
, где сумма распространяется на все заявки, пришедшие за
время ![]() .
.
Тогда, 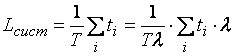
Величина ![]() есть среднее число
заявок, пришедших за время Т. Если разделить сумму всех времен
есть среднее число
заявок, пришедших за время Т. Если разделить сумму всех времен ![]() на среднее число
заявок, то получится среднее время пребывания заявки в системе
на среднее число
заявок, то получится среднее время пребывания заявки в системе ![]() .
.
Получаем, что
![]() (16)
(16)
Откуда,
![]() - формула
Литтла (17)
- формула
Литтла (17)
Таким же образом получается вторая формула Литтла: среднее время пребывания заявки в очереди равно отношению среднего числа заявок в очереди к интенсивности потока заявок:
![]() (18)
(18)