§ 4.4.2. Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний
Рассматривая Марковские процессы с дискретными
состояниями и непрерывным временем, удобно представлять, что все переходы
системы 
из состояния в
состояние происходят под действием каких-то потоков событий. Если все потоки
событий, переводящие систему из состояния в состояние, - простейшие, то
процесс, протекающий в системе, будет Марковским.
Если система находится в каком-то
состоянии 
, из которого есть непосредственный переход в другое
состояние 
(стрелка, ведущая из
состояния в на графе состояний),
то мы будем представлять так, что как будто на систему, пока она находится в
состоянии , действует простейший поток событий, переводящий ее по
стрелке 
. Как только появится первое состояние этого потока,
происходит переход системы из в .
Обозначим 
интенсивность потока
событий, переводящего систему из состояния в . Имея в своем распоряжении размеченный граф состояний
системы, легко построить математическую модель данного процесса.
Пусть система имеет 
различных состояний 
. Назовем вероятностью i-го состояния вероятность 
того, что в момент 
система будет
находиться в состоянии . Для любого момента сумма всех вероятностей состояний равна единице:
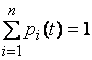
Имея в своем распоряжении размеченный граф состояний,
можно найти все вероятности состояний как функции времени.
Для этого составляют и решают так называемые уравнения Колмогорова.
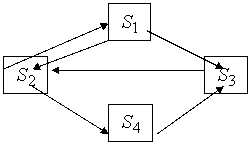
Пример. Пусть систем имеет четыре состояния: 
, размеченный граф которых имеет вид, представленный на
рисунке 25.
 |
Рис. 25. Граф состояний
Рассмотрим вероятность того, что в момент система находится в
первом состоянии. Придадим малое приращение 
и найдем 
- вероятность того,
что в момент 
система будет в
состоянии 
. Как это может произойти?
1.
в момент система уже была в
состоянии , а за время не вышла из него;
2.
в момент система была в
состоянии 
, а за время перешла из него в.
Найдем вероятность первого варианта. Вероятность того,
что в момент система была в
состоянии равна 
. Эту вероятность нужно умножить на вероятность того, что,
находившись в момент в состоянии , система за время не перейдет из него ни
в 
, ни в . Суммарный поток событий, выводящий систему из состояния , будет простейшим, с интенсивностью 
(при наложении двух
простейших потоков получается простейший поток). Значит, вероятность того, что
за время система выйдет из
состояния , равна 
; вероятность того что не выйдет: 
. Вероятность первого варианта равна 
.
Найдем вероятность второго варианта. Она равна
вероятности того, что в момент система будет в
состоянии , а за время перейдет из него в
состояние , т.е. она равна 
. Тогда,
Рассуждая аналогично для всех остальных состояний, напишем еще три дифференциальных уравнения и получим систему уравнений для вероятностей состояний:
Общее правило составление уравнений Колмогорова: левая
часть – производная вероятности 
ого состояния правая – сумма произведений вероятностей, из
которых идут стрелки в данное состояние, на интенсивности соответствующих
потоков событий, минус суммарная интенсивность всех потоков, выводящих систему
из данного состояния, умноженная на вероятность данного события.
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени.
Если при 
существует предел
вероятности для каждого из состояний, который не зависят от начального
состояния, то эти пределы называются финальными вероятностями состояний. Если
число состояний системы конечно и из каждого из них можно (за конечное число
шагов) перейти в любое другое, то финальные вероятности существуют.
Предположим, что это условие выполнено и финальные вероятности существуют:
Очевидно, что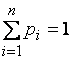 
.
Чтобы найти финальные вероятности, нужно все левые части уравнений Колмогорова приравнять нулю и решить полученную систему алгебраических уравнений. Финальную вероятность состояния можно истолковать как среднее относительное время пребывания системы в конкретном состоянии.