§ 4.4. Теория массового обслуживания
При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решения схожих задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО).
Случайный процесс, протекающий в системе, называется
Марковским, если для любого момента времени 
вероятностные
характеристики процесса в будущем зависят только от его состояния в данный
момент и не зависят от того, когда и как система пришла в это
состояние.
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например: поток вызовов на телефонной станции, поток неисправностей подвижного состава и т.д.
Интенсивность потока 
- среднее число событий приходящееся на единицу
времени. Интенсивность потока может быть как постоянной (
), так и переменной, зависящей от времени.
Поток событий называется регулярным, если событий следуют одно за другим через определенные равные промежутки времени. На практике чаще встречаются потоки не регулярные, со случайными интервалами.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. На практике часто встречаются потоки событий, которые могут считаться постоянными. Например, поток вызовов на АТС между 13 и 14 часами, практически стационарен; тот же поток в течение суток не стационарен.
Поток событий называется потоком без последействия,
если для любых двух непересекающихся участков времени 
и 
число событий,
попадающих на один из них, не зависит от того, сколько событий попало на
другой. Это означает, что события, образующие поток, появляются в те или иные
моменты времени независимо друг от друга, вызванные каждое своими собственными
причинами.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по несколько сразу. Если поток событий ординарен, то вероятностью попадания на малый участок времени двух или более событий можно пренебречь.
Поток событий называется простейшим (стационарным пуассоновским), если он обладает свойствами стационарности, ординарности и не имеет последействия.
При наложении достаточно большого числа независимых, стационарных и ординарных потоков получается поток, близкий к простейшему.
Для простейшего потока с интенсивностью интервал 
между соседними
событиями имеет показательное распределение с плотностью:
(9)
Величина в формуле (9) называется параметром показательного закона.
Для случайной величины , имеющей показательное распределение, математическое
ожидание 
есть величина,
обратная параметру, а среднее квадратическое отклонение 
равно математическому
ожиданию:
Коэффициент вариации интервалов между событиями для
показательного распределения 
. Для регулярного потока событий, у которого интервал между
событиями не случаен, коэффициент вариации равен нулю. Чем ближе 
к нулю, тем
«регулярнее» поток. Простейший поток – это «наименее регулярный» из
встречающихся на практике потоков.
Рассмотрим на оси 
простейший поток с
интенсивностью и произвольно
расположенный элементарный (очень маленький!) участок времени 
. Элементом вероятности
называется вероятность попадания на этот участок хотя бы одного события потока.
Элемент вероятности равен:
(10)
Заметим, что вероятность появления хотя бы одного
события на элементарном участке равна вероятности
появление ровно одного события на этом участке, с точностью до величин высшего порядка
малости.
Поток событий называется рекуррентным (поток Пальма), если он стационарен, ординарен, а интервалы времени между событиями представляют собой независимые случайные величины с одинаковым произвольным распределением.
Простейший поток является частным случаем рекуррентного потока. Другим частным случаем рекуррентного потока является регулярный поток событий.
Пусть в какое-то учреждение поступает простейший поток
посетителей, у входа стоит управляющий очередью, направляющий первого
посетителя к первому столу, второго – ко второму столу и т.д. Если столов 
, то на каждый из них поступает поток Эрланга -го порядка. Простейший поток есть поток Эрланга первого
порядка. При таком просеивании простейшего потока коэффициент вариации
интервалов уменьшается и поток Эрланга приближается к регулярному. Коэффициент
вариации интервалов между событиями потока Эрланга -го порядка равен 
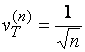. Потоки Эрланга образуют гамму потоков с различной степенью
упорядоченности – от «полного беспорядка» (простейший поток) до полной
упорядоченности (регулярный поток).
Назад к разделу "§ 4.3.3. Статическая детерминированная модель с дефицитом"