§ 4.3.3. Статическая детерминированная модель с дефицитом
Любой склад создается для того, чтобы предотвратить дефицит определенного типа изделий в обслуживаемой системе. Отсутствие запаса в нужный момент времени приводит к убыткам, которые принято называть штрафом за дефицит.
В качестве критерия эффективности управления запасами обычно выступает функция затрат, представляющая суммарные затраты на хранение и поставку запасов продукта и затраты на штрафы.
Управление запасами состоит в отыскании такой стратегии их пополнения и расхода, при которой функция затрат принимает минимальное значение.
Пусть функции 
, 
и 
выражают
соответственно пополнение запасов, их расход и спрос за промежуток времени 
. В моделях управления запасами обычно используются
производные от этих функций по времени 
, 
и 
, называемые соответственно интенсивностями пополнения,
расхода и спроса.
Если , и не являются случайными
величинами, то модель управления запасами называется детерминированной, если
хотя бы одна из функций носит случайный характер, то – стохастической. Если все
параметры модели не меняются во времени, она называется статической, иначе –
динамической. Так, модель EOQ является
статической детерминированной моделью без дефицита.
Предположим наличие дефицита. Уровень запасов в момент
времени 
определяется основным
уравнением запасов:
, где 
- начальный запас в
момент 
,
или
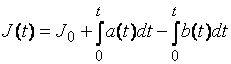
При
отсутствии запасаемого продукта, т.е. при 
спрос сохраняется с
той же интенсивностью 
, но потребление запасов отсутствует - 
, вследствие чего накапливается дефицит со скоростью 
(рисунок 24).
 |
0 
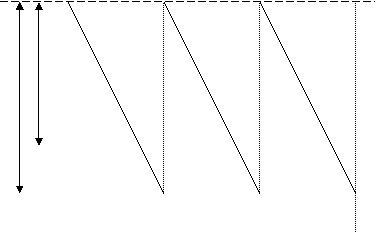
Рис. 24. Статическая модель управления запасами с дефицитом
Каждый период «пилы»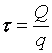 
разбивается на два
временных интервала, т.е. 
, где - время, в течение
которого производится потребление запаса; - время, когда запас
отсутствует и накапливается дефицит, который будет перекрыт в момент
поступления следующей партии.
Необходимость покрытия дефицита приводит к тому, что
максимальный уровень запаса в момент поступления
каждой партии теперь не равен ее объему , а меньше его на величину дефицита 
, накопившегося за время .
Из геометрических соображений можно установить, что
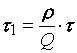
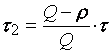
В данной модели в функцию суммарных затрат 
наряду с затратами 
(совокупные издержки
хранения) и 
(совокупные издержки
размещения и транспортировки товара) необходимо ввести затраты 
- на штраф из-за
дефицита, т.е. 
.
Мгновенные затраты хранения запаса в момент времени равны 
, тогда за промежуток времени 
они составят
,
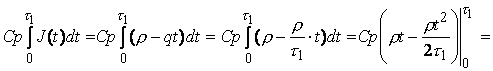
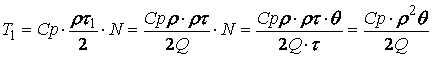где 
- затраты на хранение
единицы продукта в единицу времени
- весь рассматриваемый
промежуток времени (
).
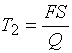
При расчете затрат будем считать, что
штраф за дефицит составляет в единицу времени 
на каждую единицу
продукта. Так как средний уровень дефицита за период равен 
, то штраф за этот период составляет 
, а за весь период :
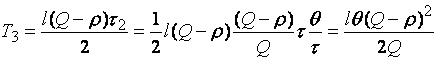
Задача сводится к отысканию такого объема партии и максимального уровня
запаса , при которых суммарные затраты принимают минимальное
значение.
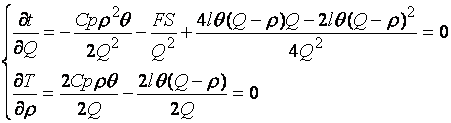
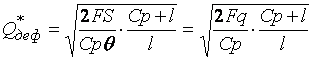
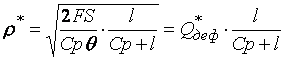
Величин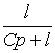а 
называется плотностью
убытков из-за неудовлетворенного спроса..
Назад к разделу "§ 4.3.2. Базовая модель оптимального уровня запасов"