§ 4.3.2. Базовая модель оптимального уровня запасов
Идея использования базовой модели EOQ, то есть, модели оптимального уровня запасов, заключается в определении такого уровня запасов, поддержание которого минимизирует совокупные издержки управления ими. При этом, совокупные издержки разбиваются на три однородные группы: издержки хранения, издержки, связанные с формированием запасов и издержки, которые возникают вследствие недостатка товарных запасов.
Рост уровня запасов сопровождается увеличением издержек хранения в прямо-пропорциональной зависимости (прямая А на рисунке 21), так как растет объем капитала, иммобилизованного в запасах, складские расходы, расходы, связанные с устареванием и порчей товаров.
Уровень издержек
 |
С
 |
А
В
0 Q*=EOQ Объем запасов
Рис. 21. Зависимость уровня издержек от объема товарных запасов
На вторую и третью группу издержек (издержки, связанные с формирование запасов и издержки, связанные с дефицитом запасов) увеличение уровня запасов оказывает противоположное действие и ведет к их снижению за счет эффекта экономии от масштаба деятельности, использования оптовых скидок поставщиков, предотвращения дефицита товарных запасов и снижения уровня обслуживания клиентов при колебании спроса. При этом, темпы снижения издержек уменьшаются с ростом уровня запасов. Закон убывания издержек управления запасами, относящихся ко второй и третьей группе, описывается кривой гиперболического вида (кривая В на рисунке 21).
Динамика совокупных издержек, являющаяся суммой
издержек перечисленных групп, определяется двумя противоположными тенденциями
при увеличении уровня запасов: одна составляющая этих издержек растет, другая –
убывает. Результирующим эффектом двух встречных процессов является характер
поведения совокупных издержек, описывающийся кривой С на рисунке 21. Их
поведение характеризуется наличием оптимальной точки 
, то есть, таким размером запасов, при котором совокупные
издержки достигают минимального уровня. Если уровень запасов меньше , то увеличение их объема ведет к снижению совокупных
издержек. Это достигается за счет того, что издержки растут медленнее, чем
издержки второй и третьей группы. В точке оптимального уровня запасов , в которой линии А и В пересекаются, темпы изменения
издержек различных групп уравновешиваются, и совокупные издержки становятся
минимальными. При дальнейшем увеличении запасов, темпы роста издержек хранения
превышают темпы снижения издержек второй и третьей группы, и совокупные
издержки возрастают.
Уровень запасов
Q
А
Время
t1 t2
Рис. 22. Динамическая схема процесса формирования и реализации товарных запасов
В соответствие с моделью EOQ, исследования по которой впервые были проведены Фордом В. Харрисом в 1915 году, при расчете оптимального размера запасов предполагается выполнение следующих основных допущений:
· спрос на товары известен и на данном промежутке времени остается постоянным;
· цена закупки товаров у поставщиков не зависит от объема закупок;
· время поставки, то есть, время между размещением заказа и поступлением товаров на склад известно и является постоянной величиной;
· при данном уровне запасов, издержки не изменяются во времени;
· поставка товаров производится одинаковыми партиями в дискретные моменты времени.
В рамках перечисленных допущений, процесс формирования и реализации товарных запасов описывается динамической схемой, представленной на рисунке 22.
Точки 
на временной оси соответствуют
моментам поставки партии товаров, величина 
на оси ординат –
объему имеющихся запасов. Угол наклона прямых, моделирующих динамику товарных
запасов, отражает скорость их реализации.
В модели оптимального уровня запасов EOQ используются следующие обозначения:
- объем реализации
товаров в год (в натуральных единицах);
- количество заказов в
год;
- размер одного
заказа;
- период реализации
партии товаров;
- средний размер
имеющихся запасов в течение года;
- цена закупки единицы
товара у поставщиков;
- средние издержки
хранения (в процентах от стоимости запасов);
- совокупные издержки
хранения;
- издержки размещения
одного заказа и его транспортировки;
- совокупные издержки
размещения и транспортировки запасов;
- совокупные издержки
управления запасами.
Размер одного заказа определяется прогнозируемым
объемом реализации товаров в год и количеством заказов: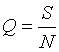 
.
Средний размер имеющихся запасов в течение периода , где 
, составляет: 
.
Тогда, совокупные издержки хранения могут быть
рассчитаны следующим образом: 
, а совокупные издержки размещения и транспортировки: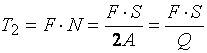 
.
В этом случае совокупные издержки управления запасами
определяются соотношением: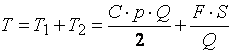 
.
Оптимальный уровень запасов , минимизирующий совокупные издержки, является решением
уравнения:
.
.
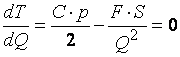
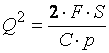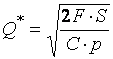После расчета оптимального уровня запасов, становится
возможным определение оптимального количества заказов в год 
и оптимальное
количество дней между заказами 
:
.
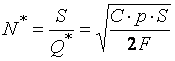
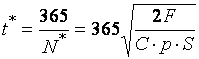Следующим важным вопросом является вычисление точки
заказа 
(orderpoint),
то есть, такого уровня запасов, после достижения которого следует размещать
заказ.
Необходимость такого расчета обусловлена тем, что между
размещением заказа и получением товаров предприятием проходит некоторый
промежуток времени, называемый периодом поставки (leadtime) 
. Если этот лаг не учитывать, возникает опасность сбоев в
реализации товаров потребителям вследствие необеспеченности предприятия
товарными запасами.
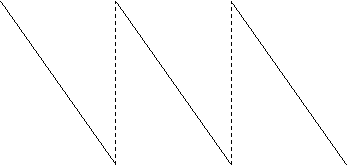
Точка заказа рассчитывается, исходя их соотношения: 
, где q – объем
реализации товаров в день, называемый коэффициентом спроса (рисунок 23).
Уровень запасов
 |
Q
tn Время
t1 t2
Рис. 23. Графическая иллюстрация расчета точки заказа
Базовая модель EOQ является наиболее распространенной и применяется большинством компаний развитых стран в качестве основы принятия решений по управлению товарными запасами.
Недостатком этой модели является довольно жесткая система исходных предпосылок, в частности, предположения о неизменности спроса, неизменности оптовых цен от объема закупаемой партии товаров и другие гипотезы.
Назад к разделу "§ 4.3.1.Системы контроля уровня запасов"
Вперед к разделу "§ 4.3.3. Статическая детерминированная модель с дефицитом"