Выбор
оптимального шага численного дифференцирования
Оценка абсолютной
погрешности численного дифференцирования складывается из остаточной
погрешности, оцениваемой величиной 
, и вычислительной погрешности, определяемой приближенным
заданием величин yi, i=0,1,...,n,
(погрешностью округления результата пренебрегаем). Рассмотрим для
определенности формулу (19).
Приближенное значение
производной
(22)
имеет остаточную погрешность
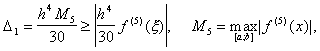
и вычислительную погрешность согласно равенству (9)
темы I
где 
- абсолютная
погрешность каждого из чисел yi, i=0,1,...,n.
Таким образом, полная
погрешность формулы численного дифференцирования (22)-
Для малости 
необходима малость h, но
при уменьшении h растет 
. Из уравнения 
получаем значение h*, при котором погрешность 
формулы (22) имеет
минимальное значение.
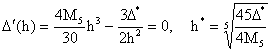
Задача.
Функция f(x)
задана таблицей своих значений, верных в написанных знаках. Найти первую
производную этой функции в точках x1*=0,7 и x2*=1,0. Оценить погрешности
результатов. Найти оптимальный шаг h* для каждой из формул
численного дифференцирования.
Xi |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
yi |
0,4794 |
0,5646 |
0,6442 |
0,7174 |
0,7833 |
0,8415 |
Решение.
Точка x1*=0,7 - центральный узел
таблицы. Для вычисления 
в данной задаче следует воспользоваться одной из формул (8),
(14), (15), (18).
1) Воспользуемся формулой
(8), обозначив x0=0,6; x1=0,7; x2=0,8. Тогда 
Остаточная погрешность
результата в соответствии с формулой (11) -
где 
Чтобы оценить M3, построим для данной
функции таблицу конечных разностей.
|
xi |
yi |
|
|
|
|
|
|
0,5 |
0,4794 |
|
|
|
|
|
|
0,0852 |
|
|
|
|||
|
0,6 |
0,5646 |
-0,0056 |
|
|
||
|
0,0796 |
-0,0008 |
|
||||
|
0,7 |
0,6442 |
-0,0064 |
-0,0001 |
|||
|
0,0732 |
-0,0009 |
|||||
|
0,8 |
0,7174 |
-0,0073 |
0,0003 |
|||
|
0,0659 |
-0,0006 |
|||||
|
0,9 |
0,7883 |
-0,0077 |
|
|||
|
0,0582 |
|
|
||||
|
1,0 |
0,8415 |
|
|
|
||
|
|
|
|
|
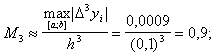
Вычислительная погрешность
результата -
где 
- абсолютная
погрешность величин yi.
Определим оптимальный шаг
для использованной формулы численного дифференцирования.
откуда
.
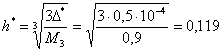2) Решим теперь данную
задачу с помощью формулы (14), обозначив x0=0,6; x1=0,7; x2=0,8; x3=0,9.
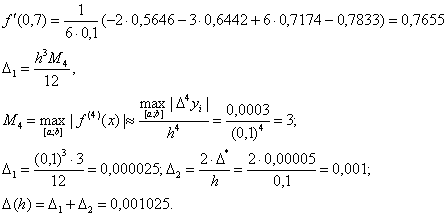
Определим для этой формулы оптимальный шаг численного
дифференцирования.
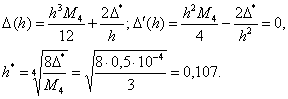
Точка x2*=1,0 является последним
узлом таблицы. Для вычисления 
служат формулы (9), (16),
(21). Воспользуемся формулой (16), обозначив x0=0,7; x1=0,8; x2=0,9; x3=1,0.
.
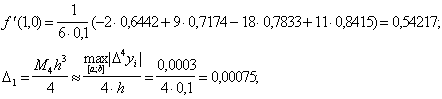
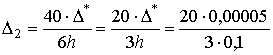Определим соответствующий
данной формуле оптимальный шаг таблицы.
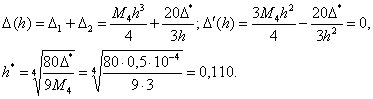
Задача
Пользуясь таблицей задачи
Б2, вычислить первую производную заданной функции в точке x* и оценить погрешность
результата. Определить оптимальный шаг таблицы
для выбранной формулы численного дифференцирования.
1. x*=1,1 2. X*=1,2 3. X*=1,3 4. X*=2,0
5. x*=2,2 6. X*=0,50 7. X*=0,52 8. X*=0,56
9. x*=0,60 10. X*=0,61 11. X*=1080 12. X*=1090
13. x*=1100 14. X*=1110 15. X*=1120 16. X*=2,70
17. x*=2,74 18. X*=2,76 19. X*=2,80 20. X*=2,84
21. x*=0,7 22. X*=0,9 23. X*=1,1 24. X*=1,3
25. x*=1,5.