Численное дифференцирование. Формулы численного дифференцирования. Погрешности, возникающие при численном дифференцировании. Выбор оптимального шага численного дифференцирования

При численном решении многих практических задач часто возникает необходимость получить значения производных различных порядков функции y=f(x), заданной в виде таблицы или в виде сложного аналитического выражения, непосредственное дифференцирование которого затруднено. В таких случаях используются приближенные методы дифференцирования.

Рассматривается следующая задача:

На сетке в узлах x_i заданы значения y_i=f(x_i) функции f(x), непрерывно дифференцируемой n+1+m раз. Требуется вычислить производную и оценить погрешность.

Один из возможных путей решения этой задачи заключается в применении теории интерполирования. Построим для функции f(x) по узлам x_i, i=0,1,...,n интерполяционный полином P_n(x) с остаточным членом R_n(x) так, что

. (1)

Продифференцируем правую и левую части соотношения (1) по x m раз и положим x=x^*

. (2)

Производная от многочлена P_n^(m)(x) применяется для приближенного представления искомой производной f^(m)(x):

. (3)

Вычисление высших производных может быть сведено к последовательному вычислению низших, поэтому мы остановимся более подробно на получении расчетных формул для . Приближенные формулы для вычисления производных в начале и в конце таблицы получаются путем дифференцирования интерполяционных многочленов Ньютона, а для вычисления производных в середине таблицы - путем дифференцирования интерполяционных многочленов Стирлинга и Бесселя.

Например, если выбрать узлы x₀,x₁,x₂,x₃,x₄ и воспользоваться первым интерполяционным многочленом Ньютона, то мы получим формулу численного дифференцирования вида

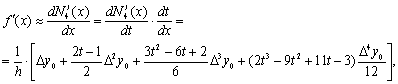(4)

где .

На практике часто выгоднее выражать значения производных не через конечные разности, а непосредственно через значения функции в узлах. Для получения таких безразностных формул удобно воспользоваться многочленом Лагранжа с равномерным расположением узлов (x_i-x_i-1=h, i=1,2,...,n).

Запишем многочлен Лагранжа второй степени (три узла интерполирования).

(5)

Тогда

(6)

В основном формулы численного дифференцирования применяют для вычисления производных в узлах x_i. Подставим в равенство (6) последовательно значения x=x₀;x₁;x₂. Получим:

;	(7)
;	(8)
.	(9)

Остаточные члены формул численного дифференцирования (7) - (9) получим дифференцированием остаточного члена

многочлена Лагранжа (5) и последовательной подстановкой в выражение для значений x=x₀;x₁;x₂.

;	(10)
;	(11)
.	(12)

Записывая интерполяционный многочлен Лагранжа третьей степени (четыре узла) и его остаточный член, получим следующие формулы для производных в узлах:

;	(13)
;	(14)
;	(15)

. (16)

В случае многочлена четвертой степени (пять узлов) получим:

;	(17)
;	(18)
;	(19)
;	(20)
	(21)

К оглавлению

Назад к разделу "Типовые задачи"

Вперед к разделу "Выбор оптимального шага численного дифференцирования"