Типовые задачи

Задача 1. Пользуясь известными значениями функциями в точках х=14,16,19,21, вычислить и оценить погрешность.

Решение. В качестве интерполяционного полинома выбираем полином Лагранжа, так как узлы интерполирования не являются равноотстоящими.

Используя формулу (8), определяем множители Лагранжа:

,, ,

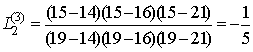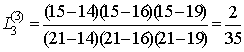
Замечание. Отметим свойство множителей Лагранжа: . Для того, чтобы найти значение функции с максимальной точностью,необходимо определить, с какой точностью следует брать значения функции в узлах, для этого определим погрешность метода, используя формулу (4):

.

Находим

,

.

Далее вычисляем минимально возможную полную погрешность результата; имеем:

.

Теперь осталось определить вычислительную погрешность:

;

учитывая формулу (9) и предполагая, что все значения функции имеют одинаковую точность , имеем:

.

То есть значения функции в узлах берем с 5 знаками после запятой.

Записав далее таблицу исходных значений с требуемой точностью, вычисляем конечный результат:

xi	14	16	19	21
f(xi)	3,74166	4,00000	4,35890	4,58258

Ответ: √15=3,872940,0001.

Задача 2.

Составить соответствующие интерполяционные полиномы и вычислить в точках x^*₁=0,63 и x^*₂=1,35 значения функции f(x)=3^x, заданной в виде следующей таблицы, содержащей значения y_i с четырьмя верными в широком смысле знаками.

xi	0,50	0,75	1,00	1,25	1,50
yi	1,732	2,280	3,000	3,948	5,196

Оценить погрешность результата.

Решение. Дополним заданную таблицу значениями конечных разностей:

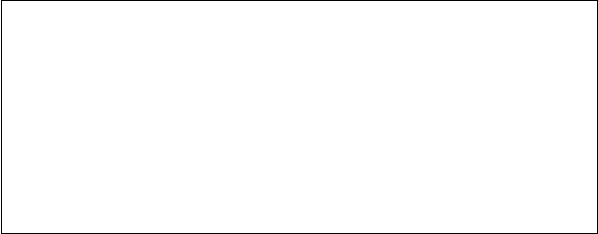x_i y_i

0,50 1,732

0,548

0,75 2,280 0,172

0,720 0,056

1,00 3,000 0,228 0,016

0,948 0,072

1,25 3,948 0,300

1,248

1,50 5,196

Так как значение x^*₁=0,63 расположено в начале таблицы, а x^*₂=1,35 - в конце ее, то для вычисления значения f(x^*₁) следует использовать первый, а для вычисления значения f(x^*₂) - второй интерполяционные полиномы Ньютона.

Отметим, что конечная разность четвертого порядка приближенно равна своей погрешности. Поэтому функцию y=3^x с точки зрения вычислительной погрешности нецелесообразно аппроксимировать полиномом степени выше третьей, и, следуя формулам (22) и (24), имеем:

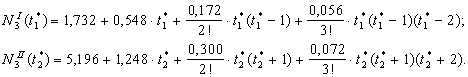
Вычислим значения t^*₁ и t^*₂.

Таким образом, получим:

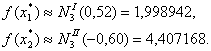
Оценим погрешности по формулам (23) и (25):

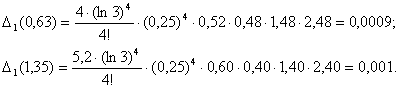
Учитывая, что все приведенные знаки у функции y=3^x верны в широком смысле, имеем:

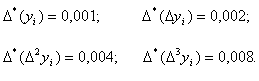
Поэтому вычислительные погрешности суть:

Округлим полученные результаты до четырех знаков.

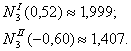
Погрешности округления равны соответственно:

Суммируя погрешность метода, вычислительную погрешность и погрешность округления, получаем:

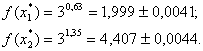
Заметим, что остаточные погрешности в данной задаче можно оценить с помощью конечных разностей. Для значения N₃^I(t₁^*) эта оценка имеет вид

а для значения N₃^II(t₂^*) -

.

Задача 3.

Функция f(x) задана таблицей своих значений, верных в написанных знаках.

xi	0, 0,6	0,7	0,8	0,9	1,0
yi	1,8221	2,0138	2,2255	2,4596	2,7183

xi	1,1	1,2
yi	3,0042	3,3201

Используя соответствующий интерполяционный полином, вычислить значения функции в точках x₁^*=0,85 и x₂^*=0,98. Оценить погрешности результатов.

Решение. Так как мы имеем достаточное количество узлов, меньших и больших x₁^* и x₂^* , то для вычисления f(x₁^*) и f(x₂^*) следует использовать интерполяционный полином Стирлинга или интерполяционный полином Бесселя, а в качестве центрального узла выбирать такой, чтобы выполнялось одно из соотношений (15) и (16). Далее, в зависимости от того, какое из двух условий выполняется, применить соответственно формулу Стирлинга или Бесселя.

В нашей задаче для вычисления f(0,85) в качестве центрального узла выберем и воспользуемся формулой Бесселя, а для вычисления f(0,98) в качестве центрального узла выберем и воспользуемся формулой Стирлинга.

Составим таблицу конечных разностей, обращая внимание на то, что если абсолютная погрешность значения y_i есть 0,5∙10^-4, то абсолютная погрешность конечных разностей порядка m есть 0,5∙10^-4∙2^m.

x_i y_i

0,6 1,8221

0,1917

0,7 2,0138 0,0200

0,2117 0,0024

0,8 2,2255 0,0224 -0,0002

0,2341 0,0022

0,9 2,4596 0,0246 0,0004

0,2587 0,0026

1,0 2,7183 0,0272 0,0002

0,2859 0,0028

1,1 3,0042 0,0300

0,3159

1,2 3,3201

0,00005 0,0001 0,0002 0,0004 0,0008

Погрешность конечных разностей четвертого порядка больше абсолютных величин значений самих этих разностей, а это означает, что с точки зрения вычислительной погрешности функцию нецелесообразно аппроксимировать полиномом степени выше третьей.

Таким образом, так как полином Бесселя строится по четному числу узлов и является полиномом нечетной степени, а полином Стирлинга строится по нечетному числу узлов и является полиномом четной степени, то для вычисления f(x₁^*) построим полином Бесселя третьей степени, а для вычисления f(x₂^*) - полином Стирлинга второй степени.

Следуя формулам (20) и (17) и учитывая, что в формуле (20) будут отсутствовать слагаемые, содержащие множитель (t-1/2),так как t₁^*=1/2, получим:

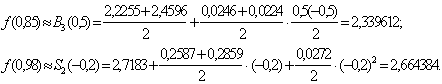
Оценим погрешности полученных результатов.

Погрешности метода равны соответственно

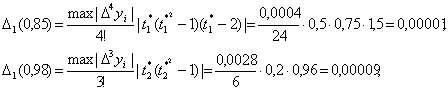
а вычислительные погрешности -

Округлим результаты до шести знаков.

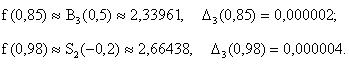
Суммируя для каждого результата погрешность метода, вычислительную погрешность и погрешность округления, получим

ƒ

Задача 4. По заданной таблице значений функции y=f(x) определить, какому значению аргумента x^* соответствуют значения функции y₁^*=2,000 и y₂^*=5,000.

Xi	0,50	0,75	1,00	1,25	1,50
yi	1,732	2,280	3,000	3,948	5,196

Решение. Так как значение y₁^*=2,000 расположено в начале таблицы, а y₂^*=5,000 - в конце ее, то для вычисления x₁^* следует использовать первый, а для вычисления x₂^* - второй интерполяционные полиномы Ньютона.

Дополним заданную таблицу значениями конечных разностей.

x_i y_i

0,50 1,732

0,548

0,75 2,280 0,172

0,720 0,056

1,00 3,000 0,228 0,016

0,948 0,072

1,25 3,948 0,300

1,248

1,50 5,196

Для определения x₁ имеем уравнение

,

а для определения x₂ -

где

Решая эти два уравнения, получим

Отсюда

Задача 5.

По заданной таблице значений функции y=f(x) определить значение x^*, для которого f(x^*)=10.

xi	10	15	17	20
yi	3	7	11	17

Решение. Функция f(x) монотонна на отрезке [10;20], следовательно, существует обратная функция x=g(y). Построим для нее интерполяционный полином L₃(y) и вычислим L₃(10).

Б1. Интерполирование с помощью полинома Лагранжа

Со сколькими верными знаками необходимо взять значение указанной функции в точках x_i, чтобы вычислить значение функции в точке x^* с минимальной погрешностью. Вычислить результат.

y=cos x; y=ln x;

1. x_i=20^o, 22^o, 25^o, 26^o; x^*=23^o. 21. x_i=2; 2,5; 3; 4; x^*=e.

2. x_i=27^o, 28^o, 30^o, 32^o; x^*=29^o. 22. x_i=10, 13, 14, 16; x^*=11.

3. x_i=30^o, 31^o, 33^o, 35^o; x^*=32^o. 23. x_i=11, 13, 16, 18; x^*=12.

4. x_i=35^o, 38^o, 40^o, 43^o; x^*=37^o. 24. x_i=1, 2, 4, 5; x^*=e.

5. x_i=40^o, 45^o, 48^o, 51^o; x^*=43^o. 25. x_i=5, 6, 8, 9; x^*=7.

y=sin x; y=lg x;

5. x_i=7^o, 9^o, 14^o, 17^o; x^*=12^o. 11. x_i=6, 8, 11, 12; x^*=10.

6. x_i=15^o, 18^o, 21^o, 23^o; x^*=20^o. 12. x_i=9, 12, 15, 19; x^*=10.

7. x_i=17^o, 22^o, 25^o, 30^o; x^*=28^o. 13. x_i=98, 102, 107, 112; x^*=100.

8. x_i=25^o, 29^o, 34^o, 37^o; x^*=30^o. 14. x_i=110, 115, 119, 121; x^*=113.

9. x_i=40^o, 45^o, 51^o, 55^o; x^*=50^o. 15. x_i=115, 119, 124, 128; x^*=120.

16. x_i=14, 16, 19, 21; x^*=17.

17. x_i=15, 18, 21, 23; x^*=20.

18. x_i=12, 14, 17, 19; x^*=16.

19. x_i=20, 22, 26, 29; x^*=25.

20. x_i=8, 10, 11, 13; x^*=9.

Б2. Интерполирование с помощью формул Ньютона,

Стирлинга, Бесселя

Используя таблицу значений функции (все приведенные знаки верны в узком смысле):

а) составить таблицу конечных разностей;

б) вычислить значения функции для указанных значений аргументов и оценить погрешность результатов.

xi	yi	1. x1^*=1,18; x2^*=1,38;
1,1	0,89121	x3^*=1,25; x4^*=2,16.
1,2	0,93204	2. x1^*=1,12; x2^*=1,46;
1,3	0,96356	x3^*=1,55; x4^*=2,18.
1,4	0,98545	3. x1^*=1,16; x2^*=1,57;
1,5	0,99750	x3^*=1,65; x4^*=2,17.
1,6	0,99957	4. x1^*=1,15; x2^*=1,75;
1,7	0,99166	x3^*=1,88; x4^*=2,14.
1,8	0,97385	5. x1^*=1,17; x2^*=1,66;
1,9	0,94630	x3^*=1,95; x4^*=2,15.
2,0	0,90930
2,1	0,86321
2,2	0,80850

xi	yi	6. x1^*=0,504; x2^*=0,524;
0,50	1,6487	x3^*=0,535; x4^*=0,604.
0,51	1,6653	7. x1^*=0,503; x2^*=0,533;
0,52	1,6820	x3^*=0,545; x4^*=0,603.
0,53	1,6989	8. x1^*=0,502; x2^*=0,542;
0,54	1,7160	x3^*=0,555; x4^*=0,602.
0,55	1,7333	9. x1^*=0,506; x2^*=0,556;
0,56	1,7507	x3^*=0,565; x4^*=0,606.
0,57	1,7683	10. x1^*=0,508; x2^*=0,568;
0,58	1,7860	x3^*=0,575; x4^*=0,608.
0,59	1,8040
0,60	1,8221
0,61	1,8404

xi	yi	11. x1^*=1013; x2^*=1043;
1010	3,00432	x3^*=1065; x4^*=1113.
1020	3,00860	12. x1^*=1012; x2^*=1032;
1030	3,01284	x3^*=1055; x4^*=1112.
1040	3,01703	13. x1^*=1014; x2^*=1054;
1050	3,02119	x3^*=1075; x4^*=1114;
1060	3,02531	14. x1^*=1016; x2^*=1066;
1070	3,02938	x3^*=1085; x4^*=1116.
1080	3,03342	15. x1^*=1018; x2^*=1078;
1090	3,03743	x3^*=1095; x4^*=1118.
1100	3,04139
1110	3,04532
1120	3,04922
xi	yi	16. x1^*=2,706; x2^*=2,756;
2,70	0,3704	x3^*=2,77; x4^*=2,906.
2,72	0,3676	17. x1^*=2,708; x2^*=2,768;
2,74	0,3650	x3^*=2,87; x4^*=2,908.
2,76	0,3623	18. x1^*=2,709; x2^*=2,769;
2,78	0,3597	x3^*=2,81; x4^*=2,909.
2,80	0,3571	19. x1^*=2,712; x2^*=2,772;
2,82	0,3546	x3^*=2,85; x4^*=2,912.
2,84	0,3521	20. x1^*=2,715; x2^*=2,835;
2,86	0,3497	x3^*=2,89; x4^*=2,915.
2,88	0,3472
2,90	0,3448
2,92	0,3425

xi	yi	21. x1^*=0,63; x2^*=0,88;
0,6	1,8221	x3^*=1,05; x4^*=1,63.
0,7	2,0138	22. x1^*=0,68; x2^*=0,93;
0,8	2,2255	x3^*=1,25; x4^*=1,68.
0,9	2,4596	23. x1^*=0,64; x2^*=1,07;
1,0	2,7183	x3^*=1,45; x4^*=1,64.
1,1	3,0042	24. x1^*=0,67; x2^*=1,22;
1,2	3,3201	x3^*=1,15; x4^*=1,67.
1,3	3,6693	25. x1^*=0,66; x2^*=1,34;
1,4	4,0552	x3^*=0,95; x4^*=1,66.
1,5	4,4817
1,6	4,9530
1,7	5,4739

Б3. Обратное интерполирование (случай неравноотстоящих узлов)

По таблице задачи Б1 определить значение аргумента x^*, соответствующее указанному значению y^* функции f(x).

1. y^*=0,914 2. y^*=0,857 3. y^*=0,829

4. y^*=0,777 5. y^*=0,695 6. y^*=0,175

7. y^*=0,326 8. y^*=0,391 9. y^*=0,454

10. y^*=0,743 11. y^*=0,93 12. y^*=1,15

13. y^*=2,02 14. y^*=2,07 15. y^*=2,09

16. y^*=3,873 17. y^*=4,062 18. y^*=4,243

19. y^*=4,9 20. y^*=3,5 21. y^*=0,8

22. y^*=2,5 23. y^*=2,7 24. y^*=1,1

25. y^*=2

Б4. Обратное интерполирование (случай равноотстоящих узлов)

По таблице задачи Б2 определить значение аргумента x^*, соответствующее указанному значению y^* функции f(x).

1. y^*=0,81 2. y^*=0,82 3. y^*=0,83

4. y^*=0,84 5. y^*=0,86 6. y^*=1,7

7. y^*=1,75 8. y^*=1,8 9. y^*=1,65

10. y^*=1,83 11. y^*=3,008 12. y^*=3,010

13. y^*=3,046 14. y^*=3,035 15. y^*=3,040

16. y^*=0,35 17. y^*=0,36 18. y^*=0,37

19. y^*=0,345 20. y^*=0,361 21. y^*=3,2

22. y^*=2 23. y^*=3 24. y^*=4

25. y^*=5

К оглавлению

Назад к разделу "Обратное интерполирование"

Вперед к разделу "Численное дифференцирование. Формулы численного дифференцирования. Погрешности, возникающие при численном дифференцировании. Выбор оптимального шага численного дифференцирования"