Обратное
интерполирование
Постановка задачи.
Рассмотрим функцию y=f(x), непрерывную на интервале [a,b], заданную в
виде таблицы своих значений yi для соответствующих значений аргумента xi.
Необходимо найти, в какой точке x* из интервала (xk-1,xk) значение функции равно y* из
интервала (yk-1,yk).
При этом предполагается, что интервал (xk-1,xk) настолько мал, что значение x* будет
единственным.
Фактически мы имеем дело с задачей определения корня
уравнения:
. (26)
Одним из возможных путей решения этой задачи является
аппроксимация функции f(x) интерполяционным полиномом Pn(x) и замена
уравнения (26) уравнением:
(27)
Действительный корень
уравнения (27)
является приближенным значением корня X* уравнения (26).
Поэтому принимаем, что 
.
Погрешность значения 
определяется двумя моментами: построением интерполяционного
полинома и решением уравнения (27) и может быть представлена в виде:
, (28)
где 
- суммарная
погрешность интерполирования,
,
- погрешность решения уравнения (27).
Если заданных значений функции, для которых надо найти
соответствующие значения аргументов, много, то имеет смысл пользоваться
следующим способом решения задачи обратного интерполирования.
Пусть существует гладкая функция x=g(y), обратная к f(x), непрерывная
со своими производными на минимальном интервале, содержащем значения yi=f(xi), i=0,1,.... В
этом случае достаточно вычислить значение обратной функции g(y) в точке y*,
используя методы прямого интерполирования, т.е. 
.
Остаточную погрешность полученного значения Ln(y*) можно согласно (4) оценить следующим образом
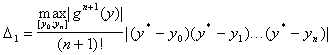. (29)
Оценка вычислительной погрешности в этом случае будет
иметь более сложный по сравнению с (9) вид, поскольку от приближенных величин y0,y1,...,yn зависят теперь
множители Лагранжа
.
Приведенный способ является более эффективным в
сравнении с ранее изложенным. Однако его недостатком является требование гладкой функции g(y), что далеко
не всегда выполняется.