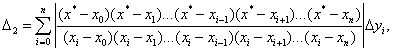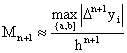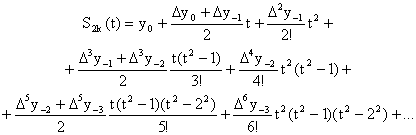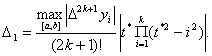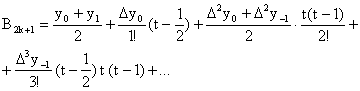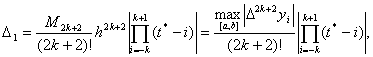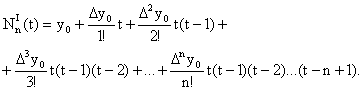Интерполирование.
Постановка задачи интерполирования. Полином Лагранжа, Стирлинга, Бесселя,
Ньютона. Обратное интерполирование
Рассмотрим функцию y=f(x), непрерывную на интервале [a ,b] и заданную некоторыми своими значениями yi=f(
xi ), i=0,1, . . . ,n для
соответствующих значений аргумента a£x0<x1<.
. . <xn£b. Необходимо найти значение этой функции в точке x*Î[a ,b], x*¹xi и оценить
погрешность полученного приближенного значения.
Один из возможных путей решения
поставленной задачи заключается в следующем:
1) для функции f(x)
по значениям yi в узлах
xi , i=0,1, . . . ,n строится
многочлен степени не выше n
|
Pn(x) = a0 ×xn +a1×xn-1+. . .+an-1×x+an , |
(1) |
принимающий в точках xi значения yi , т.е.
значения коэффициентов многочлена - ai - находятся из условия:
Pn(xi ) = yi , i=0,1, . . . , n .
Этот многочлен называется интерполяционным. Он всегда
существует и единственен.
Функция
f(x) представляется в виде: f(x)= Pn(x ) + Rn(x),
(2)
где
Rn(x) - остаточный член интерполяционной формулы. Если функция f(x)
имеет непрерывную производную порядка (n+1)
на [a,b], то
|
|
(3) |
2) Вычисляется значение Pn(x*). Если
значения yi заданы приближенно или же по каким-либо причинам вычисления не могут быть выполнены абсолютно
точно, то фактически вычисляется лишь приближенное значение ![]() для точного значения Pn(x*).
для точного значения Pn(x*).
3) Приближенно принимается, что f(x*) » ![]() n(x*).
n(x*).
4) Оценивается погрешность метода по
остаточному члену интерполяционной формулы:
|
|
(4) |
|
где |
(5) |
5) Оценивается погрешность вычисления
по погрешностям приближенных значений исходных данных:
|
D2 ³ ½ Pn(x*) - |
(6) |
Таким образом, полная погрешность приближенного
значения есть
|
D ³ D1 + D2 ³ ½f(x*) - |
(7) |
Для достаточно гладких функций и
достаточного количества узлов на интервале интерполирования погрешность метода
будет достаточно мала. При достаточной точности исходных значений yi и
достаточной точности вычислений ![]() вычислительная
погрешность будет также достаточно мала; следовательно, приближенное значение
вычислительная
погрешность будет также достаточно мала; следовательно, приближенное значение ![]() в этом случае будет
достаточно мало отличаться от точного значения f(x*).
в этом случае будет
достаточно мало отличаться от точного значения f(x*).
При решении практических задач
интерполяционный многочлен строят в различных формах.
Одна из таких форм - интерполяционный полином Лагранжа:
|
|
(8) |
Остаточная погрешность значения Ln(x*), вычисленного по формуле (8),
оценивается формулой (4), а вычислительная погрешность
|
|
(9) |
где Dyi - погрешность исходных данных (значений функции в
узлах).
Обычно
интерполяционный полином составляется не по всем узлам таблицы, а лишь по
некоторым, находящимся вблизи x*.
В случае равноотстоящих узлов, то есть
когда
|
xi = x0 + i ×h ,
i=0,1,...,n, |
(10) |
где h -
шаг интерполяции, целесообразно
использовать интерполяционные полиномы Стирлинга, Бесселя и Ньютона.
Для более компактной записи этих
полиномов обычно вводят понятие конечных разностей.
Будем называть конечными разностями
первого порядка функции y=f(x) в точке xi следующие величины :
|
Dyi = yi+1 – yi , |
(11) |
а
конечные разности к–го порядка определяются такими
рекуррентными соотношениями :
|
D k
yi = Dk-1
yi+1 - Dk-1
yi . |
(12) |
Конечные разности функции y=f(x) удобно записать в виде таблицы 1 :
Таблица 1
|
xi |
yi |
Dyi |
D2yi |
D3yi |
D4yi |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
x -2 |
y -2 |
|
|
|
|
|
|
|
Dy -2 |
|
|
|
|
x-1 |
y -1 |
|
D2y -2 |
|
|
|
|
|
Dy -1 |
|
D3y -2 |
|
|
x 0 |
y 0 |
|
D2y-1 |
|
D4y -2 |
|
|
|
Dy 0 |
|
D3y -1 |
|
|
x 1 |
y 1 |
|
D2y 0 |
|
|
|
|
|
Dy 1 |
|
|
|
|
x 2 |
y 2 |
|
|
|
|
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
Например,
|
xi |
Yi |
Dyi |
D2yi |
D3yi |
D4yi |
|
30° |
0,5000 |
|
|
|
|
|
|
|
0,0736 |
|
|
|
|
35° |
0,5736 |
|
-0,0044 |
|
|
|
|
|
0,0692 |
|
-0,0005 |
|
|
40° |
0,6428 |
|
-0,0049 |
|
0 |
|
|
|
0,0643 |
|
-0,0005 |
|
|
45° |
0,7071 |
|
-0,0054 |
|
0,0002 |
|
|
|
0,0589 |
|
-0,0003 |
|
|
50° |
0,7660 |
|
-0,0057 |
|
-0,0004 |
|
|
|
0,0532 |
|
-0,0007 |
|
|
55° |
0,8192 |
|
-0,0064 |
|
|
|
|
|
0,0468 |
|
|
|
|
60° |
0,8660 |
|
|
|
|
Если все исходные значения yi заданы
с одной и той же погрешностью D*, то эта погрешность распространяется на разности
порядка m с коэффициентом 2m и быстро
растет с ростом m :
D*(Dmyi) = 2m×D* (это легко показать, если вспомнить определение
погрешностей арифметических действий). А так как соответствующие конечные
разности Dm yi будут убывать с ростом m, то наступит такая ситуация, когда все погрешности конечных
разностей станут сравнимы или больше самих конечных разностей, и их
использование станет нецелесообразным. Поэтому порядок последних конечных
разностей, которые еще целесообразно использовать в вычислениях, называют
порядком правильности таблицы конечных разностей, который, в свою очередь,
определяет максимально допустимый порядок интерполяционного полинома,
строящегося для данной функции с заданным шагом интерполирования.
Обратимся вновь к формуле (4) оценки
остаточной погрешности интерполяционного полинома. На практике точно определить
производную f(n+1)(x) и ее максимальное по
модулю значение Mn+1 бывает, как правило,
невозможно, так как функция обычно задается лишь в виде таблицы своих значений.
Поэтому прибегают к приближенной оценке Mn+1 . Известно, что для функций, m раз непрерывно дифференцируемых,
конечные разности порядка по m
включительно обладают следующим свойством :
Dm yi = h m × f(m)(x) , xÎ(xi , xi +m).
На
основании этого свойства
|
|
(13) |
Перейдем к рассмотрению названных форм
интерполяционных полиномов для функции y=f(x),
заданной своими значениями yi в узлах xi равномерной сетки с шагом h.
Интерполяционный
полином Бесселя и Стирлинга.
Пусть точка x* расположена вблизи от некоторого узла, который
назовем x0 .
Для
интерполирования выберем узлы, симметричные относительно x0:
. . . x-k , .
. . , x-1 , x0 ,
x1 , .
. . , xk , .
. .
Введем в рассмотрение новую переменную
|
|
(14) |
Выбор полинома осуществляется исходя из
требования получения минимальной величины погрешности интерполяции и
определяется величиной ½t*½:
|
Если |
(15) |
то используется полином
Стирлинга, если
0,25< t*<0,75
, - (16)
полином
Бесселя.
Одно из условий (15) или (16) может
быть обеспечено выбором соответствующего узла таблицы в качестве x0 . При этом полином Стирлинга - полином
четной степени - строится по нечетному числу узлов; полином Бесселя - нечетной
степени - строится по четному числу узлов.
Итак, интерполяционный полином
Стирлинга строится в виде:
|
|
(17) |
Оценка (4) остаточной погрешности
значения S2k( t*)
может быть представлена в виде
|
|
(18) |
или, согласно(13), -
|
|
|
Оценим теперь вычислительную погрешность результата
![]()
Как было сказано выше, абсолютная погрешность конечной
разности порядка m есть 2m ×D*,
поэтому
|
D2 = D*( 1+2 | t*| +2t*2 +...) |
(19) |
Если выполняется условие (16), то есть
точка интерполирования находится вблизи середины отрезка между узлами x0 и x1 (если так пронумерованы эти узлы), и
строится полином нечетной степени, то следует использовать узлы, симметричные
относительно середины отрезка между x0 и x1 , то
есть относительно точки t=1/ 2.
Интерполяционный полином Бесселя для
узлов
. . . x-k , .
. . , x-1 , x0 , x1 , x2 ,
. . . , xk ,
xk+1
, . . .
строится
в следующем виде :
|
|
(20) |
Оценки остаточной и вычислительной погрешностей
результата
B2k+1( t*)
имеют соответственно следующий вид :
|
|
(21) |
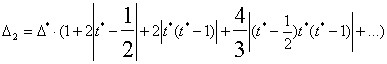
Интерполяционные полиномы Ньютона
I и II интерполяционные полиномы Ньютона используют
для определения значений функции в точках, находящихся соответственно в начале
и конце таблицы интерполирования. В этом случае не всегда имеется возможность
выбора достаточного количества узлов (слева или справа) для построения
необходимых конечных разностей S2k , B2k+1 .
Пусть точка x* расположена вблизи первого узла
интерполирования x0 на
сетке x0 , x1 , . .
. , xn. Тогда следует использовать
первую интерполяционную формулу Ньютона :
|
|
(22) |
t
определяется формулой (14);
x0 - ближайший к x* узел
слева.
Оценки погрешностей приближенного значения ![]() могут быть представлены в виде:
могут быть представлены в виде:
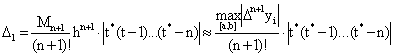 (23)
(23)
![]()
Если точка интерполирования x* расположена вблизи последнего узла сетки x0,x1,...,xn ,
то используют второй интерполяционный полином Ньютона:
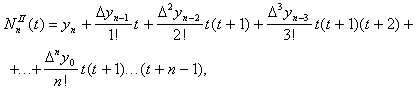 (24)
(24)
где
xn - ближайший к x* узел
справа, ![]() .
.
Оценки погрешностей приближенного значения NnII(t*) можно записать в виде:
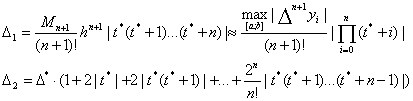 (25)
(25)
Назад к разделу "Содержание тем курса «Вычислительная математика»"