Содержание
тем курса «Вычислительная математика»
Тема 1. Погрешность результата численного решения задачи.
Источники и классификация погрешностей. Абсолютная и относительная погрешности.
Погрешность функции. Обратная задача теории погрешностей.
Тема 2. Приближение функций. Постановка задачи приближения
функций. Классы аппроксимирующих функций. Критерии согласия. Погрешность
аппроксимации.
Интерполяционные методы приближения функций.
Алгебраическое интерполирование. Многочлен Лагранжа и его остаточный член.
Оптимизация узлов интерполирования. Многочлены Чебышева. Разделенные разности и
их свойства. Интерполяционные многочлены Ньютона с разделенными разностями.
Конечные разности и их свойства. Интерполяционные многочлены Ньютона, Стирлинга
и Бесселя. Интерполирование с кратными узлами. Обратное интерполирование.
Интерполяция и приближение сплайнами.
Тема 3. Численное дифференцирование. Вывод формул численного
дифференцирования. Остаточная погрешность. Вычислительная погрешность при
численном дифференцировании и выбор оптимального шага таблицы производных.
Тема 4. Численное интегрирование. Простейшие квадратурные
формулы. Квадратурные формулы Ньютона-Котеса. Оценка погрешности квадратурной
формулы. Повышение точности интегрирования за счет разбиения отрезка на части.
Интегрирование функций с заданной степенью точности. Практическая оценка
погрешности. Правило Рунге. Квадратурные формулы Гаусса.
Тема 5. Решение нелинейных уравнений и методы одномерной
оптимизации. Отделение корней: правило кольца, теорема Лагранжа, теорема
Штурма. Уточнение корней: метод итераций, метод Ньютона, метод хорд. Постановка
задачи одномерной оптимизации. Поиск отрезка, содержащего точку экстремума.
Дихотомический поиск. Метод золотого сечения. Метод средней точки (бисекции).
Метод хорд. Метод ДСК-Пауэлла. Метод кубической аппроксимации. Метод
Ньютона-Рафсона.
Тема 6. Численные методы алгебры. Метод Гаусса с выбором
главного элемента. Итерационные методы решения систем линейных алгебраических
уравнений. Метод простой итерации, условия его сходимости. Оценка погрешности.
Тема 7. Основные понятия численных методов решения
обыкновенных дифференциальных уравнений. Постановка задачи. Численные методы
решения задачи Коши. Методы Рунге-Кутта. Контроль погрешности на шаге. Понятие
о конечноразностных методах. Экстраполяционная и интерполяционная формулы
Адамса.
Вопросы по курсу
"Вычислительная математика"
1. Математические характеристики точности приближенных
чисел.
2. Общая формула погрешностей.
3. Погрешность арифметических действий.
4. Обратная задача теории погрешностей.
5. Интерполяционный многочлен Лагранжа.
6. Оценка
погрешностей многочлена Лагранжа.
7. Конечные разности и их свойства.
8. Интерполяционныe формулы Ньютона.
9. Интерполяционные формулы Стирлинга и Бесселя.
10. Обратное интерполирование.
11. Численное дифференцирование.
12. Формулы численного дифференцирования, основанные
на формулах Ньютона.
13. Формулы численного дифференцирования, основанные
на формуле Стирлинга.
14. Численное интегрирование. Формула прямоугольников.
15. Формула трапеций.
16. Формула Симпсона.
17. Интегрирование с заданной степенью точности.
18. Решение алгебраических и трансцендентных
уравнений. Отделение корней.
19. Метод половинного деления. Алгоритм.
20. Метод хорд.
21. Метод Ньютона.
22. Метод итераций.
23. Метод Свенна.
24. Метод дихoтомического
поиска.
25. Метод золотого сечения.
26. Метод средней точки.
27. Метод секущих (одномерная оптимизация).
28. Метод Ньютона-Рафсона.
29. Метод Гаусса с выбором главного элемента.
30. Метод простой итерации.
31. Метод Эйлера.
32. Метод Эйлера-Коши.
33. Метод Рунге-Кутта.
34. Метод Адамса.
Введение
Программа обучения предусматривает выполнение
студентами по курсу "Вычислительная математика" одной контрольной
работы. Эта контрольная работа состоит из 13 типовых задач, охватывающих
слудующие разделы курса:
1) приближенные вычисления - задачи
А1,А2;
2) интерполирование функций - задачи Б1,
Б2, Б3, Б4;
3) численное дифференцирование - задача
В;
4) численное интегрирование функций -
задача Г;
5) решение нелинейных уравнений - задачи
Д1, Д2;
6) решение систем линейных уравнений -
задачи Е1, Е2;
7) решение дифференциальных уравнений -
задача Ж.
Для каждой из задач (А1, А2, Б1, Б2, Б3, Б4, В, Г, Д1,
Д2, Е1, Е2, Ж) предложено 25 вариантов. Номером варианта студента является
остаток от деления пятизначного шифра (номер зачетной книжки) на 25.
Методические указания и типовые задачи. Приближенные
вычисления
Числа точные и приближенные. Характеристики
приближенных чисел. Общая формула погрешности. Обратная задача теории погрешностей.
Решение большинства практических задач с определенной
степенью условности можно представить в виде двух последовательных этапов:
1) математическое описание рассматриваемой проблемы;
2) решение сформулированной математической задачи.
На первом этапе мы встречаемся с двумя характерными
источниками погрешности. Во-первых, это то, что реально протекающие процессы не
всегда можно точно описать математически, а вводимые значения дают возможность
получить лишь более или менее идеализированные модели. Во-вторых, это
неточность задания исходных параметров, получаемых, как правило, из
эксперимента, дающего лишь приближенный результат.
В соответствии с этим суммарная погрешность
математической модели и начальных данных объединяется в погрешность исходной информации.
Имея в виду независимость этой погрешности от второго
этапа решения исходной задачи, ее часто называют НЕУСТРАНИМОЙ ПОГРЕШНОСТЬЮ.
Получение точного решения математической задачи
(второй этап) независимо от того, строится ли оно аналитически или на ЭВМ, как
правило, не осуществимо. Поэтому в практических расчетах используются методы
получения приближенных решений и, в первую очередь - численные.
Такая вынужденная замена точного решения приближенным
и порождает ПОГРЕШНОСТЬ МЕТОДА, или, как ее часто называют, ПОГРЕШНОСТЬ
АППРОКСИМАЦИИ.
Наконец, в процессе решения задачи мы производим
округление исходных данных, промежуточных и окончательных результатов. Эти
погрешности, а также погрешности, возникающие при выполнении арифметических
операций над приближенными числами, в той или иной мере переносятся в результат
вычислений и образуют так называемую
ВЫЧИСЛИТЕЛЬНУЮ ПОГРЕШНОСТЬ или ПОГРЕШНОСТЬ ОКРУГЛЕНИЙ.
В связи со сказанным при постановке задачи либо
указывается требуемая точность окончательного результата, то есть задается
погрешность, максимально допустимая в процессе решения математической задачи,
либо ограничиваются требованием подсчета суммарной погрешности результата.
В практике вычислений часто возникает необходимость в
округлении числа, то есть в замене его другим числом с меньшим количеством
цифр, причем сохраняется одна или несколько цифр, считая слевa направо.
Сформулируем ПРАВИЛА ОКРУГЛЕНИЯ, которыми мы будем
пользоваться в дальнейшем.
1. Если отбрасываемые цифры составляют число, большее
половины единицы последнего оставляемого разряда, то последняя оставляемая
цифра усиливается (увеличивается на единицу).
Если отбрасываемые цифры составляют число, меньшее
половины единицы последнего оставляемого разряда, то оставляемые цифры остаются
без изменения.
2. Если же отбрасываемые цифры составляют число,
равное половине единицы последнего оставляемого разряда, то последняя
оставляемая цифра усиливается, если она нечетная, и остается без изменения,
если она четная.
Пример.
Числа А1 = 273,25001; A2 = 2,71828; A3 = 273,15; =
273,25 округлить до десятых долей.
Решение.
Следуя правилу округления, имеем
a1 = 273,3; a2 =
2,7; a3 = 273,2; a4 = 273,2.
В повседневной практической деятельности, а также при
решении той или иной математической задачи используются числа двух родов:
ТОЧНЫЕ и ПРИБЛИЖЕННЫЕ.
ПРИБЛИЖЕННЫМ ЧИСЛОМ ![]() для точного числа А
называется число, незначительно отличающееся от точного и заменяющего его в вычислениях.
для точного числа А
называется число, незначительно отличающееся от точного и заменяющего его в вычислениях.
Определение 1. АБСОЛЮТНОЙ ПОГРЕШНОСТЬЮ D![]() приближенного числа
приближенного числа ![]() называется величина,
не меньшая абсолютного значения разности между точным числом А и его
приближенным значением
называется величина,
не меньшая абсолютного значения разности между точным числом А и его
приближенным значением ![]() :
:
D![]() ³½
³½![]() -A½. (1)
-A½. (1)
Таким образом, точное число А заключено в границах :
![]()
![]() - D
- D![]() £ А £
£ А £ ![]() + D
+ D![]() .
.
Этот факт сокращенно можно записать так :
А = ![]() ± D
± D![]() .
.
Определение 2. ОТНОСИТЕЛЬНОЙ ПОГРЕШНОСТЬЮ d![]() приближенного числа
приближенного числа ![]() называется величина,
определяемая неравенством :
называется величина,
определяемая неравенством :
|
|
(2) |
Таким образом, за относительную погрешность
числа ![]() можно принять
можно принять
|
|
(3) |
Всякое положительное число ![]() можно представить в
следующем виде:
можно представить в
следующем виде:
![]() , (4)
, (4)
где ![]() - десятичные цифры
числа
- десятичные цифры
числа ![]() (a
(a![]() = 0,1,...,9), причем
= 0,1,...,9), причем ![]() ¹ 0, а m - целое
число, называемое старшим десятичным разрядом числа
¹ 0, а m - целое
число, называемое старшим десятичным разрядом числа ![]() .
.
Определение 3. ЗНАЧАЩИМИ ЦИФРАМИ числа называются все цифры, кроме нулей, стоящих
левее первой отличной от нуля цифры.
Нули, записанные в конце числа, всегда значащие (в
противном случае их не пишут).
Например, числа 0,001406; 5,0300 имеют соответственно
4 и 5 значащих цифр.
Если же мы хотим показать, что у числа 400000 только
два значащих нуля, то это число следует записать в виде произведения двух
сомножителей: 400×103 , или 0,400×106. Последняя форма записи называется нормальной и
является предпочтительной.
Определение 4. Цифры ![]() приближенного числа
приближенного числа ![]() называются ВЕРНЫМИ В
СМЫСЛЕ w , если абсолютная
погрешность числа
называются ВЕРНЫМИ В
СМЫСЛЕ w , если абсолютная
погрешность числа ![]() не пpевосходит w единиц разряда последней верной цифры:
не пpевосходит w единиц разряда последней верной цифры:
|
D |
(5) |
При
w = 1 (w = 0,5) цифры ![]() называются верными в
широком(узком) смысле.
называются верными в
широком(узком) смысле.
Аналогичного рода зависимость можно установить между
количеством верных значащих цифр и относительной погрешностью:
|
|
(6) |
Рассмотрим ОБЩУЮ ЗАДАЧУ ТЕОРИИ ПОГРЕШНОСТЕЙ.
Вычисляется значение функции n переменных ![]() в некоторой точке А(А1,A2,...,Аn), координаты которой известны лишь
приближенно. Требуется определить получающуюся при этом погрешность.
в некоторой точке А(А1,A2,...,Аn), координаты которой известны лишь
приближенно. Требуется определить получающуюся при этом погрешность.
Приведем одно из возможных решений сформулированной
задачи. Пусть ![]() i и D
i и D![]() i (i = 1,2,...,n) есть приближенные
значения и их погрешности для координат точки А, а u =¦(a1,а2,...,аn) - приближенное значение искомой величины U = ¦ (А1,A2,...,Аn). Применяя
теорему Лагранжа о приращении функции, для абсолютной величины разности точного
и приближенного значений можно получить следующую оценку:
i (i = 1,2,...,n) есть приближенные
значения и их погрешности для координат точки А, а u =¦(a1,а2,...,аn) - приближенное значение искомой величины U = ¦ (А1,A2,...,Аn). Применяя
теорему Лагранжа о приращении функции, для абсолютной величины разности точного
и приближенного значений можно получить следующую оценку:
![]() , (7)
, (7)
где 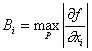 , а область Р есть
область возможных значений координат
, а область Р есть
область возможных значений координат
Аi : Р = {Аi : ![]() ; i
=1,2,...,n}.
; i
=1,2,...,n}.
Если функция ¦ имеет
непростую структуру, то получение Вi может оказаться сложной задачей. Поэтому,
используя малость области P
изменения параметров , в практических расчетах полагают
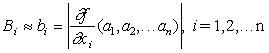
и ![]() (8)
(8)
Рассмотрим, какой вид приобретет формула (8)
применительно к некоторым функциям, наиболее часто встречающимся в практике
расчетов.
1.
Алгебраическая сумма приближенных слагаемых -
f (x1,x2,...,xn) = x1 ± x2 ± ... ± xn :
![]() .
(9)
.
(9)
2.
Произведение приближенных множителей -
f( x1 , x2 , ... , xn ) = x1 ×× x2 × ... × xn :
![]() .
(10)
.
(10)
3.
Частное –
![]() ; (11)
; (11)
du = ![]() .
.
4.
Степень-
f(x) = xm , m>0
; (12)
du = m ×d![]() .
.
5.
Корень -
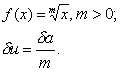 (13)
(13)
В вычислительной практике важное значение имеет
ОБРАТНАЯ ЗАДАЧА ТЕОРИИ ПОГРЕШНОСТЕЙ - определение допустимых погрешностей
приближенных значений аргументов, позволяющих вычислить значение функции с
погрешностью, не превышающей заданного e.
В такой постановке задача является неопределенной,
поскольку можно найти бесчисленное множество значений D![]() i ,
обеспечивающих выполнение неравенства
i ,
обеспечивающих выполнение неравенства
D u £ e . (14)
Поэтому необходимо наложить дополнительные требования
на искомые величины D![]() i,,
диктуемые конкретной ситуацией.
i,,
диктуемые конкретной ситуацией.
Например, потребуем, чтобы вклад в суммарную
погрешность каждого слагаемого левой части (14) был одинаков, то есть
b1D![]() £e/ n .
£e/ n .
Выписанное условие часто называют ПРИНЦИПОМ РАВНЫХ
ВЛИЯНИЙ, для которого очевидно
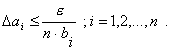 (15)
(15)
В случаях, когда все аргументы имеют одинаковую
размерность, можно предположить, что
![]() .
.
Эти условия называют ПРИНЦИПОМ РАВНЫХ АБСОЛЮТНЫХ
ПОГРЕШНОСТЕЙ, согласно которому из соотношения (14) имеем
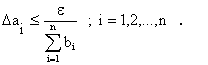 (16)
(16)
Аналогично можно построить ПРИНЦИП РАВНЫХ
ОТНОСИТЕЛЬНЫХ ПОГРЕШНОСТЕЙ, определяемый соотношениями
![]() . (17)
. (17)
Следуя условию (17), из соотношения (14) имеем:
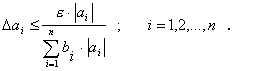 (18)
(18)
Типовые задачи
Задача 1. Дано приближенное число ![]() = 88,325 и известно, что у этого числа три верных значащих
цифры в широком(узком) смысле. Оценить абсолютную и относительную погрешность в
обоих случаях.
= 88,325 и известно, что у этого числа три верных значащих
цифры в широком(узком) смысле. Оценить абсолютную и относительную погрешность в
обоих случаях.
Решение. Поскольку у числа ![]() три верные цифры в
широком(узком) смысле, то абсолютная погрешность данного числа не превосходит
единицы (половины единицы) последнего верного разряда, т.е.
три верные цифры в
широком(узком) смысле, то абсолютная погрешность данного числа не превосходит
единицы (половины единицы) последнего верного разряда, т.е.
D![]() £ w × 10 m-n+1 =
0,1 ×w =
£ w × 10 m-n+1 =
0,1 ×w =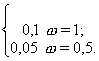
d![]() £
£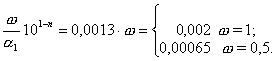
Задача 2. Дано приближенное число ![]() = 2,7182 и его абсолютная погрешность D
= 2,7182 и его абсолютная погрешность D![]() = 0,007.
= 0,007.
Определить,
какие значащие цифры приближенного числа будут верными в широком(узком) смысле.
Решение. В силу соотношения (5) имеем:
0,007 £ w × 10 0-n+1.
Решение
этого неравенства есть
n £ 3 при w = 1;
n £ 2 при w = 0,5.
Таким образом, у приближенного числа ![]() = 2,7182 по крайней мере три верных знака в широком смысле и
два верных знака в узком смысле. Про остальные цифры мы не можем сказать,
верные они или нет.
= 2,7182 по крайней мере три верных знака в широком смысле и
два верных знака в узком смысле. Про остальные цифры мы не можем сказать,
верные они или нет.
Задача 3. Дано приближенное число ![]() = 2,7182 и его
относительная погрешность d
= 2,7182 и его
относительная погрешность d![]() = 1% .
= 1% .
Определить,
какие значащие цифры приближенного числа будут верными в широком(узком) смысле.
Решение.
Определим ![]() »0,028 и потребуем выполнения неравенства (5):
»0,028 и потребуем выполнения неравенства (5):
0,028 £ w × 10-n+1.
Решив это неравенство, получим
n £ 2 при
w = 1 и w = 0,5 .
Таким образом, у приближенного числа по
крайней мере два верных знака в широком и узком смысле. Про остальные цифры мы
не можем сказать, верные они или нет.
Задача 4. Со сколькими верными знаками
в широком(узком) смысле следует вычислить
![]() = 4,… , чтобы
= 4,… , чтобы
а) абсолютная погрешность не
превышала 0,007;
б) относительная погрешность не
превышала 1%?
Решение.
а) Если у приближенного числа будет n
верных знаков в смысле w, то его абсолютная погрешность не будет превышать w × 10 m-n+1.
Поэтому n следует выбрать таким ,
чтобы выполнялось неравенство:
w× 10 m-n+1 £ e ,
принимающее
для данной задачи следующий вид :
w× 10 -n+1 £ 0,007 .
Решая его при w = 1 , получаем
n ³ 4 , а при
w = 0,5 - n ![]() .
.
Следовательно, для того, чтобы
абсолютная погрешность приближенного числа ![]()
![]() не превышала 0,007,
необходимо взять не менее четырех верных знаков в широком смысле: 4,582 (или трех верных знаков в узком смысле:
4,58).
не превышала 0,007,
необходимо взять не менее четырех верных знаков в широком смысле: 4,582 (или трех верных знаков в узком смысле:
4,58).
б)
Если у приближенного числа ![]() будет n верных знаков в смысле w, то его относительная погрешность не будет превышать
будет n верных знаков в смысле w, то его относительная погрешность не будет превышать ![]() . Поэтому n следует
выбрать таким , чтобы выполнялось неравенство:
. Поэтому n следует
выбрать таким , чтобы выполнялось неравенство:
![]() ,
,
принимающее для данной задачи
следующий вид:
![]() .
.
Решая его при w = 1 и w = 0,5, получаем один и тот же результат:
n ³3. Следовательно, для того, чтобы относительная
погрешность приближенного значения ![]() не превышала 1%, необходимо
взять не менее трех верных знаков в широком и узком смысле: 4,58.
не превышала 1%, необходимо
взять не менее трех верных знаков в широком и узком смысле: 4,58.
Задача 5. Вычислить значение ![]() и оценить абсолютную
погрешность результата, взяв приближенные значения аргументов с четырьмя
верными знаками.
и оценить абсолютную
погрешность результата, взяв приближенные значения аргументов с четырьмя
верными знаками.
Решение. В формулу для вычисления y входят три приближенных
аргумента: x1 =![]() , x2 = p, x3
= e. Bозьмем их значения с четырьмя верными знаками.
, x2 = p, x3
= e. Bозьмем их значения с четырьмя верными знаками.
x1 = 2,236
; x2 = 3,142 ; x3
= 2,718
D x1 = D x2 = D![]() 0,0005.
0,0005.
Вычислим приближенное значение функции
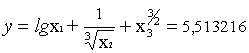 .
.
Согласно
(8)
Dy = b1 Dx1
+ b2 Dx2+ b3 Dx3 , где
![]()
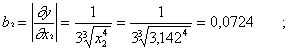
![]()
и,
следовательно,
Dy =
(0,1924 + 0,0724 + 2,4730) × 0,0005 = 0,00137.
Итак, результат y
=5,513216 имеет абсолютную
погрешность Dy =0,00137,
т.е. три верных знака.
Задача 6. С каким числом верных знаков
следует взять значения аргументов функции 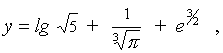 чтобы вычисленное значение этой функции имело 4 верных знака?
чтобы вычисленное значение этой функции имело 4 верных знака?
Решение. Исходя из приближенных
значений ![]()
![]() x3= e =2,7, определим
приближенные значения функции и ее частных производных.
x3= e =2,7, определим
приближенные значения функции и ее частных производных.
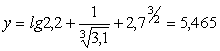 ;
;
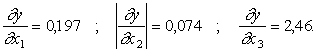
Абсолютная
погрешность величины y удовлетворяет
неравенству (5):
![]()
Используя предположение о равенстве абсолютных
погрешностей аргументов, имеем, согласно (16) :
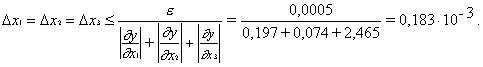
Таким образом, каждый из приближенных аргументов
следует взять с пятью верными знаками.
Задача 7. Вычислить значение функции 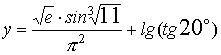 и оценить абсолютную
погрешность результата, взяв значения аргументов с четырьмя верными знаками.
и оценить абсолютную
погрешность результата, взяв значения аргументов с четырьмя верными знаками.
Решение. В формулу для вычисления y входят четыре аргумента: ![]()
![]()
![]()
![]() Их приближенные значения с четырьмя верными знаками: x1=2,718 ; x2
= 2,222 ; x3 = 3,142
; x4 = 0,3640 ; Dx1=
D x2= D x
Их приближенные значения с четырьмя верными знаками: x1=2,718 ; x2
= 2,222 ; x3 = 3,142
; x4 = 0,3640 ; Dx1=
D x2= D x![]() = 0,0005; Dx4=
0,00005.
= 0,0005; Dx4=
0,00005.
Представим функцию y как сумму двух функций:
y = y1
+ y2 ,
где
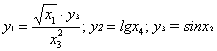 .
.
Вычислим
приближенные значения этих функций
y3 = sin 2,222 = 0,7954;
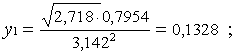
y2=lg0,3640= - 0,4389;
y=y1+y2= -0,3061.
Согласно
(8)
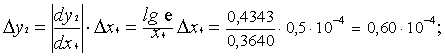
![]()
Абсолютную погрешность Dy1 выразим
через относительную
Dy1 = d y1×½y1½,
а
для вычисления d y1 удобно
воспользоваться равенствами (10), (12), (13) :
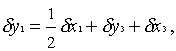
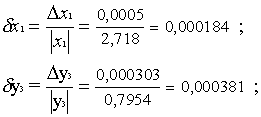
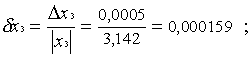
d y1= 1/2 × 0,000184 +
0,000381 + 2 × 0,000159 = 0,000791;
![]() = 0,1328 × 0,000791 = 0,000105.
= 0,1328 × 0,000791 = 0,000105.
Согласно (9) имеем
Dy= Dy1 +
Dy2 =0,000105
+0,000060 = 0,000165.
Таким образом, приближенное значение y = - 0,3061 имеет три верных знака.
Задача 8. С каким числом верных знаков
следует взять значения аргументов функции ![]() , чтобы вычисленное значение функции имелo три верных знака?
, чтобы вычисленное значение функции имелo три верных знака?
Решение. Положим, как в задаче 7, x1 = e , x2 = ![]() , x3 = p,
, x3 = p,
x4 = tg20° ; y = y1+y2 ;
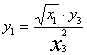 ;
y2= lg x4 ; y3 = sin
x2 . Взяв
предварительно приближенные аргументы с двумя верными знаками:
;
y2= lg x4 ; y3 = sin
x2 . Взяв
предварительно приближенные аргументы с двумя верными знаками:
x1 = 2,7; x2=
2,2; x3= 3,1;
x4 = 0,36 , вычислим приближенные
значения функций:
y3 = sin 2,2 = 0,79
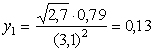
y2 = lg 0,36 = -0,44
y = y1 + y2 = 0,13 - 0,44 = -0,31.
По условию (5)
![]() .
.
Воспользовавшись
(9) имеем
Dy = D y1 +D y2 £ 0,0005
откуда, предполагая, что D y1 = D y2 получим
согласно (8)
![]()
и D x4 £ 0,00025 × ln 10 × x4 = 0,00025 ×2,303 × 0,35 = 0,00020.
Вычислим теперь предельно допустимое значение для
относительной погрешности dy1 . Т.к. 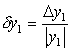 , а D y1 £ 0,00025 , то
, а D y1 £ 0,00025 , то
dy1 £ 0,00025/½y1½= 0,00025/0,13 = 0,0019 .
Согласно
(10)
dy1= 0,5dx1+dy3+2dx3 £ 0,0019.
Предполагая,
что dx1 = dy3 = d x3, получим
dx1 = dy3 = dx3 £ 0,0019/3,5 = 0,00054.
Для
x1 имеем
D x1 = dx1 × |x1| £ 0,00054 × 2,7 = 0,0014...
Для y3 =
sin x2
D y3 =
dy3 × |y3| £ 0,00054 × 0,79 = 0,00042...
но D y3 = |cos x2| × |x2| ,
откуда
![]()
Для
x3 - D x3 = dx3 × |x3| £ 0,00054 × 3,1 = 0,0016...
Итак, получили: D x1 £ 0,0014... ; D x2 £ 0,00071... ; D x3 £ 0,0016... ;
D x4 £ 0,00020... ; откуда следует, что значения всех
аргументов необходимо взять с четырьмя верными знаками.
А1. Прямая задача теории погрешностей
Вычислить значение выражения, беря значения аргументов
с четырьмя верными знаками. Оценить погрешность результата.
1. ![]() ; 2.
; 2. ![]() ;
;
3. ![]() ; 4.
; 4. ![]() ;
;
5. ![]() ; 6.
; 6.
![]() ;
;
7. ![]() ; 8.
; 8. ![]() ;
;
9.![]() ; 10.
; 10. ![]() ;
;
11. ![]() ; 12.
; 12. ![]() ;
;
13.![]() ; 14.
; 14.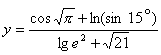 ;
;
15.![]() ; 16.
; 16.![]() ;
;
17.![]() ; 18.
; 18. ![]() ;
;
19. ![]() ;
;
20. ![]() ; 21.
; 21. ![]() ;
;
22. ![]() ; 23.
; 23. ![]() ;
;
24. ![]() ; 25.
; 25. ![]() .
.
A2. Обратная задача теории погрешностей
С каким числом верных знаков следует взять значения
аргументов функции из задачи А1, чтобы значение этой функции имело четыре
верных знака?