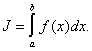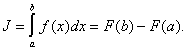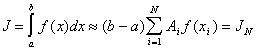Численное интегрирование

Постановка задачи. Пусть требуется вычислить интеграл

(1)

Если функция f(x) является непрерывной на отрезке [a;b], то интеграл (1) существует и может быть вычислен по формуле Ньютона-Лейбница

(2)

Однако для большинства функций f(x) первообразную F(x) не удается выразить через элементарные функции. Кроме того, функция f(x) часто задается в виде таблицы ее значений для определенных значений аргумента. Все это порождает потребность в построении формул численного интегрирования, или квадратурных формул.

Определение 1. Приближенное равенство

(3)

называется квадратурной формулой, определяемой узлами и коэффициентами A_i.

Величина

(4)

называется остаточным членом квадратурной формулы.

В зависимости от способа задания подынтегральной функции f(x) будем рассматривать два различных в смысле реализации случая численного интегрирования.

Задача 1. На отрезке [a;b] в узлах x_i заданы значения f_i некоторой f, принадлежащей определенному классу F. Требуется приближенно вычислить интеграл (1) и оценить погрешность полученного значения.

Так обычно ставится задача численного интегрирования в том случае, когда подынтегральная функция задана в виде таблицы.

Задача 2. На отрезке [a;b] функция f(x) задана в виде аналитического выражения. Требуется вычислить интеграл (1) с заданной предельно допустимой погрешностью.

Рассмотрим алгоритмы решения задач 1 и 2.

Алгоритм решения задачи 1.

1. Выбирают конкретную квадратурную формулу (3) и вычисляют J_N. Если значения функции f(x_i) заданы приближенно, то фактически вычисляют лишь приближенное значение для точного J_N.

2. Приближенно принимают, что .

3. Пользуясь конкретным выражением для остаточного члена или оценкой его для выбранной квадратурной формулы, вычисляют погрешность метода

.

4. Определяют погрешность вычисления

,

по погрешностям приближенных значений f(x_i).

5. Находят полную абсолютную погрешность приближенного значения :

6. Получают решение задачи в виде

.

Алгоритм решения задачи 2.

1. Представляют в виде суммы трех неотрицательных слагаемых

,

где - предельно допустимая погрешность метода; - пре-дельно допустимая погрешность вычисления ; - предельно допустимая погрешность округления результата.

2. Выбирают N в квадратурной формуле так, чтобы выполнялось неравенство

.

3. Вычисляют f(x_i) с такой точностью, чтобы при подсчете J_N по формуле (3) обеспечить выполнения неравенства

.

Для этого, очевидно, достаточно вычислить все f(x_i) с абсолютной погрешностью

.

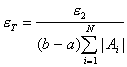4. Найденную в п.3 величину округляют (если )
с предельно допустимой погрешностью до величины .

5. Получают решение задачи в виде

.

К оглавлению

Назад к разделу "Выбор оптимального шага численного дифференцирования"

Вперед к разделу "Построение простейших квадратурных формул"