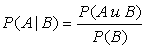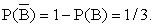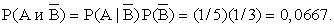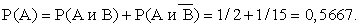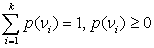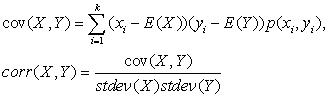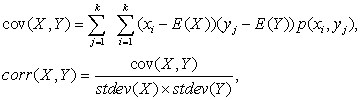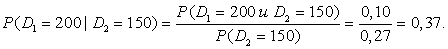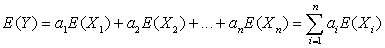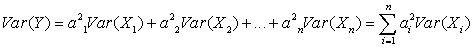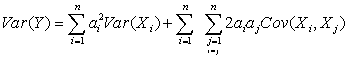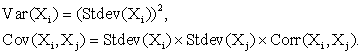Практически все экономические переменные связаны с неопределенностью, например, объемы спроса, время между приходом покупателей в супермаркет, рыночные стоимости акций, котировки валют и так далее. В математической статистике и теории вероятностей такие величины называются случайными переменными. Полный набор вероятностей всех значений называется распределением вероятностей.

Цель данной темы представить все основные понятия, связанные с вероятностью, а также инструменты для работы с распределениями вероятностей и их обобщающими показателями, к которым относятся: математическое ожидание, дисперсия, стандартное отклонение, ковариация, корреляция. В предыдущем разделе мы приводили их выборочные аналоги.

Вероятность некоторого события имеет значение от 0 до 1 и означает степень ожидания данного события. «0» — событие точно не произойдет, «1» — событие точно произойдет.

Пусть A — некоторое событие, Ā — событие, состоящее в том, что событие 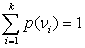не произойдет. Тогда правило дополнения состоит в том, что:

P(Ā) = 1 — P(A)

Назовем события взаимно исключающими, если одновременно может состояться не более одного из этих событий. Назовем набор взаимно исключающих событий полным, если одно из них обязательно должно произойти. Если события A₁ …A_n взаимно исключающие, то справедливо следующее правило, которое и называется аддитивным правилом или правилом сложения:

P (произойдет по крайней мере одно из событий A₁ …A_n ) = P(A₁ ) +…+ P(A_n )

Если набор событий является полным, то эта вероятность равна 1.

Вероятность зависит от имеющейся информации. Условная вероятность — формальный способ отображение этой зависимости. Пусть Р(А) и Р(В) вероятности событий А и В. Если нам уже известно, что событие В произошло, тогда логично предположить, что вероятность события А в этом случае может измениться. Эта измененная вероятность называется условной вероятностью и обозначается как Р (А|В). Тогда правило условной вероятности записывается в виде:

Иногда удобно использовать производное правило, которое называется мультипликативным правилом, или правилом умножения:

Р(А и В) = Р(А|В) Р(В)

Пример

Компания «Строймонтаж» занимается поставками стройматериалов. Компания имеет контракт с одним из клиентов со сроком до конца июля. Однако выполнение этого срока зависит от того, получит ли компания необходимые материалы от одного из своих поставщиков до середины июля. Сейчас 1 июля. Как можно количественно оценить неопределенность в данной ситуации?

Решение

Пусть событие А состоит в том, что компания «Строймонтаж» выполняет контракт к концу июля, а событие В состоит в том, что она получает материалы от поставщика к середине июля. В начале июля компания оценивает вероятность события В как 2/3, то есть Р(В) = 2/3. Кроме этого, компания оценивает вероятность Р(А|В) = 3/4.

Р(А и В) = Р(А|В)Р(В) = (3/4)(2/3) = 0,5.

Вычислим некоторые другие вероятности в этой задаче.

Пусть компания «Строймонтаж» оценивает вероятность 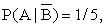тогда:

Далее вычислим итоговую вероятность того, что контракт будет выполнен в срок.

С понятием условной вероятности тесно связано понятие вероятностной независимости. Это означает, что вероятность одного события никак не связано с вероятностью другого. В этом случае выполняется соотношение:

Р(А и В) = Р(А) Р(В)

Часто независимость событий определяется исходя из эмпирических данных. Пример с событиями: «первым в семье рождается мальчик» и «вторым в семье рождается мальчик».

Часто понятия теории вероятности демонстрируются на примере равновероятных событий: бросание монеты, игральные кости, рулетка, урны с шарами. Однако реальные случайные исходы редко бывают равновероятными, например, различные сценарии развития компании.

Существуют два типа случайных величин: дискретные (конечное число значений) и непрерывные (бесконечное число значений). Вычисление обобщающих характеристик для непрерывных случайных величин требует определенной математической техники. Пусть дискретная случайная величина может принимать k значений 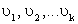с вероятностями 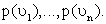Тогда требования к вероятностям можно выразить как:

Вычисляются следующие обобщающие показатели.

Математическое ожидание, которое часто обозначают как μ:

Для определения меры разброса значений вычисляют дисперсию и стандартное отклонение:

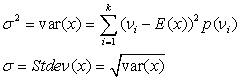
Пример

Инвестор вкладывает деньги в некоторый финансовый инструмент сроком на один год и ожидает некоторый процент дохода (или убытков) в предстоящем году от данного вложения. Он полагает, что возможны пять общих сценариев развития национальной экономики в предстоящем году: быстрый рост, умеренный рост, отсутствие роста, умеренный спад и резкий спад. Далее из всей имеющейся информации удалось сделать предположение, что ожидаемые уровни доходов соответственно равны 0,23; 0,18; 0,15; 0,09 и 0,03, то есть доход колеблется от 23 до 3%. Кроме этого удалось оценить вероятности этих сценариев: 0,12; 0,40; 0,25; 0,15 и 0,08. Используя данную информацию, вычислим математическое ожидание и стандартное отклонение для ожидаемого дохода инвестора в предстоящем году.

Решение

Обозначим случайную величину «уровень доходов предстоящего года» как X. Каждое значение этой случайной величины соответствует определенному сценарию. Так, υ₁ = 0,23 и p(υ₁ ) = 0,12 (см. файл ДОХОД.XLS (шаблон и решение). Основной рабочий лист модели представлен на рис. 51.

Далее построим вычисления по следующему плану.

1. Среднеожидаемый доход (=СУММПРОИЗВ (Доходности; Вероятности));

2. Квадраты отклонений (=(С4-МатОжидание)^2);

3. Дисперсия (=СУММПРОИЗВ (КвОтклонений; Вероятности));

4. Стандартное отклонение (=КОРЕНЬ (Дисперсия)).

Математическое ожидание в данном случае подразумевает усредненную величину, как если бы ситуация повторялась бы много раз.

Откуда появляются вероятности событий? В частности, вероятности из предыдущего примера. Можно говорить об объективных и субъективных вероятностях.

Так, вероятности, связанные с бросанием монеты, игральных костей или вращением рулетки можно отнести к категории объективных. Они либо вычисляются (если монеты, кости, рулетка идеальные), или получаются многократным повтором ситуации и усреднением результата.

Напротив вероятности, связанные с экономическими явлениями, не допускают использования данной методики (оцениваемая ситуация может быть уникальной). В этом случае опираются на ожидания экспертов или на некоторые аналогии из прошлого опыта. Такие вероятности принято относить к категории субъективных.

Поскольку мнения экспертов могут сильно расходиться, могут расходиться и конечные результаты. Именно поэтому отдельно исследуют вопрос о зависимости результатов от начальных данных (анализ чувствительности). Примеры анализа чувствительности будут рассмотрены в разделе 3.

Довольно часто возникает ситуация, когда необходимо, зная распределение некоторой случайной величины X, построить распределение или вычислить обобщающие характеристики некоторой случайной величины Y, являющейся функцией от X. Рассмотрим конкретный пример.

Пример

Книжный магазин планирует заказать партию Рождественских календарей. Планируется их продажа по цене 15 руб. за экземпляр. Есть возможность сделать только один заказ. Если спрос окажется меньше, чем заказанное количество, остаток партии придется сдать во вторичную переработку (так как она уже практически не реализуема). Если наоборот, то часть потенциальных покупателей будет безвозвратно потеряна. Магазин оценивает спрос в пределах от 250 до 400 экземпляров. Опираясь на мнения ряда экспертов и опыт аналогичных рождественских акций предыдущих лет, магазин оценивает распределение спроса следующим образом (B10:C16) (см. файл КАЛЕНДАРИ.XLS (шаблон и решение). Если магазин закажет 350 экземпляров, какова вероятность, что они будут распроданы? Каков в этом случае среднеожидаемый доход?

Решение

Пусть D — спрос, S — количество проданных календарей, R — доход. План решения задачи следующий:

• определим количество проданных календарей с помощью функции =МИН(B10; Имеется), поместив ее в ячейках В20 — В26;

• вычислим доход по формуле =Цена*B20, поместив ее в ячейках С20 — С26;

• определим вероятности по формуле =С10, поместив ее в ячейке D20 и скопировав ее в D20 — D26;

• вычислим средние ожидаемые значения для спроса, количества проданных календарей и дохода по формуле (для дохода) =СУММПРОИЗВ(Выручка; Вероятности);

• вычислим дисперсии и стандартные отклонения для спроса, количества проданных календарей и дохода.

Результаты вычислений представлены на рис. 52.

Замечание. Вероятность продажи 350 есть сумма 0,25 + 0,15 + 0,10 = 0,50.

Логическим продолжением исследования данной модели является рассмотрение значений выходных характеристик при различных объемах заказа. Такой анализ можно сделать с помощью таблицы подстановки, которая описывается в следующем примере. Рассматривая две основные характеристики — ожидаемый доход и стандартное отклонение дохода, можно построить следующие зависимости от размера заказа (рис. 53).

Однако данная модель не учитывает ряд важных обстоятельств. Так, например, не учитывается возможный эффект уменьшения цены с ростом размера заказа, затраты связанные со стоимостью транспортировки, хранения, замораживания определенных финансовых вложений в товаре и так далее.

В заключение данного параграфа рассмотрим случай, когда производная случайная величина задается линейной функцией от заданной. Приведем явные формулы вычисления обобщающих показателей для линейной функции. Пусть Y = a + bX, тогда:

E(Y) = α + bE(X),

Var(Y) = b² Var(X),

Stdeυ(Y) = bStdeυ(X).

Под сценарным типом распределения двух случайных величин будем понимать ситуацию, когда значения, принимаемые случайными величинами, жестко связаны (соответствуют некоторым сценариям).

Рассмотрим два обобщающих показателя — ковариацию и корреляцию, которые отражают степень линейной зависимости двух случайных величин. Ранее приводили формулы для выборочной ковариации и корреляции. Ниже приведены точные формулы для сценарного подхода:

где p(x_i , y_i ) — совместная вероятность. Обратите внимание, что именно в силу сценарного типа распределения в формулах присутствует только один индекс, соответствующий номеру сценария.

Как мы уже отмечали в части 1 коэффициент корреляции всегда заключен в пределах от -1 до 1, то есть:

-1 ≤ corr(X,Y) ≤ 1.

Следующий пример демонстрирует сценарный тип распределения.

Пример

Инвестор планирует сделать инвестиции в акции некоторой компании и в золото. Он полагает, что доходности этих инвестиций в предстоящем году зависят от общего состояния экономики. Для упрощения ситуации он рассматривает четыре возможных сценария: депрессия, легкий спад, нормальное состояние и бум. Анализируя имеющуюся информацию, он полагает вероятности этих сценариев равными 0,05; 0,30; 0,50; 0,15. Для каждого состояния экономики он оценивает доходность по акциям и по золоту (см. файл АКЦИИ-ЗОЛОТО.XLS (шаблон и решение). Например, в случае состояния депрессии инвестор прогнозирует падение курса акций на 20% и рост цены на золото на 5%. Инвестор хочет исследовать совместное распределение доходности по этим двум видам инвестиций. Он также хочет проанализировать распределение в портфеле по этим видам инвестиций.

Решение

Возможны только четыре сочетания доходностей по акциям и золоту, которые определяются четырьмя сценариями развития экономики. Далее отдельно вычисляем средние значение, дисперсию и стандартное отклонение для доходов по акциям и золоту с помощью известной функции. Например, среднеожидаемое значение дохода от 1 рубля, вложенного в акции, вычисляется как: =СУММПРОИЗВ(АкцДоходн;Вероятности).

Общий вид модели представлен на рис. 54.

Далее выполним следующие шаги:

• вычислим ожидаемые отклонения от среднего по формуле С5-АкцСредн и разместим результаты в ячейках В15 — В18, используя копирование ячеек;

• вычислим ковариацию для доходностей по акциям и золоту, используя функцию СУММПРОИЗВ(АкцОткл; ЗлОткл; Вероятности);

• вычислим коэффициент корреляции по формуле Ковар/(АкцСтОткл*ЗлСтОткл).

Отрицательный знак коэффициента корреляции означает, что доходности по акциям и золоту имеют в некоторой мере противоположные тенденции.

Далее нам необходимо исследовать распределение средств между акциями и золотом. Предположим, что инвестируется 10 000 руб. Предположим, что часть средств (ячейка В6) инвестируется в акции, а остальная — в золото (рис. 55). Поскольку сценариев только 4, возможных доходностей тоже 4, например:

Доходность для легкого спада = 0,6*0,10 + 0,4*0,20 = 0,14.

Таким образом, мы можем вычислить распределение доходностей портфеля (см. файл АКЦИИ-ЗОЛОТО.XLS (шаблон и решение).

Интересно проследить зависимость между доходностью портфеля и стандартным отклонением этой доходности от доли вложений в акции. Для этого разместим формулы =С18 и =С20 в ячейки В24 и С24, сформируем массив значений параметра, например, с шагом 0,1, выделим массив А24:С35, выберем команду Данные / Таблица подстановки… и введем ячейку В6, как ячейку заполнения Подставлять значение по строкам. В результате мы получим таблицу соответствующих значений ожидаемых доходностей портфеля и их стандартные отклонения (рис. 55).

Далее воспользовавшись Мастером диаграмм, отобразим полученные результаты графически (рис. 56).

График полученной зависимости показывает, что доходность портфеля постоянно растет с ростом доли акций в портфеле, однако стандартное отклонение (которое часто используется в качестве меры риска) первоначально убывает, а потом (после доли 0,4) возрастает. Следовательно, можно утверждать, что по крайней мере 40% акций иметь в портфеле целесообразно. Вопрос о целесообразности большей доли решается более сложными методами, выходящими за рамки данной темы. Как мы видим из полученных результатов, существует баланс между доходностью и риском.

В предыдущем разделе рассматривали две случайные величины, распределенные по сценарному типу. В данном случае рассматриваем всевозможные пары (x, y) значений двух случайных величин X и Y. Фиксируя какое-либо значение x или y, можем строить распределение условной вероятности для другой случайной величины.

Приведем точные формулы для теоретической ковариации и корреляции в общем случае:

где p(x_i , y_j ) — совместная вероятность, то есть вероятность события, что случайные величины примут одновременно свое i-е и j-е значение соответственно.

Пример

Компания реализует два вида продукции, являющиеся взаимозаменяемыми. Некоторые покупатели предпочитают продукт первого вида, а некоторые второго. Компания располагает данными по вероятностям спроса на товары обоих видов (см. файл СОВМЕСТНЫЙ СПРОС.XLS (шаблон и решение). Используя данную информацию, представим более полную вероятностную информацию о спросе на оба вида продукции.

Решение

Таблица исходных совместных вероятностей представлена на рис. 57. Обозначим величины спросов на данные виды продукции как D₁ и D₂ .

Сначала вычислим маргинальные вероятности по каждому из продуктов, то есть вероятности значений каждого из спросов. Для этого просуммируем столбцы и строки (рис. 57)

Однако полученные маргинальные распределения никак не отражают взаимосвязь между спросами на эти два вида продукции. Эта взаимосвязь в принципе видна из таблицы совместных вероятностей, но ее не достаточно удобно интерпретировать. Поэтому вычислим таблицы условных вероятностей по каждому виду продукции.

Сначала вычислим условные вероятности для спросов на первый продукт при фиксированных спросах на второй (строки 15—19) (рис. 58). Приведем пример расчета:

Эти условные вероятности вычисляются одновременно по формуле =С5/$G5, которая помещается в ячейку С15 и распространяется на массив С15:F19.

Аналогично вычислим условные вероятности для спросов на второй продукт при фиксированных спросах на первый (строки 21—29) (рис. 58). Эти условные вероятности вычисляются одновременно по формуле =С5/С$10, которая помещается в ячейку С24 и распространяется на массив С24:F28.

Кроме этого, может быть вычислен ряд обобщающих характеристик (рис. 59).

Математические ожидания по каждому из спросов вычисляются по маргинальным распределениям в ячейках В32 и С32 с помощью формул =СУММПРОИЗВ(Спрос1;Вероятн1), =СУММПРОИЗВ(Спрос2;Вероятн2).

Дисперсии и стандартные отклонения спросов вычислим следующим образом. Например, для нахождения характеристик по продукту 1 сделаем следующее: введем формулу =(С4-СреднСп1)^2 в ячейку С36 и скопируем ее до ячейки F36. Далее введем в ячейку В44 формулу =СУММРОИЗВ(КвОтклСп1;Вероятн1) и извлечем из нее квадратный корень в ячейке В45.

Ковариации и корреляции спросов. Сначала рассчитаем отклонения от среднего. Для этого в ячейку С37 введем формулу =(С$4-СреднСп1)*($B5-СреднСп2) и скопируем ее в массив С37:F41. Затем вычислим ковариацию в ячейке В47 с помощью формулы =СУММПРОИЗВ(ПроизвОтклСп;СовмВер).

Далее рассчитаем коэффициент корреляции в ячейке В48 по формуле =КоварСп/(СтандСп1*СтандСп2).

Если нас интересуют зависимости между спросами на эти два вида продукции, то имеет смысл отобразить эти зависимости графически, используя возможности Мастера диаграмм (рис. 60 и 61).

Важным частным случаем совместных распределений случайных величин является случай, когда случайные величины являются независимыми. Как правило, на практике хотя бы слабая зависимость есть, но иногда мы можем сделать предположение о независимости с целью облегчения анализа. В этом случае выполняется соотношение Р(X=x и Y=y) = P(X=x)*P(Y=y).

Пример

Дистрибьютор запасных частей постоянно следит за уровнем запасов по каждой позиции в конце каждой недели. Если количество деталей определенного вида опускается до или ниже определенного уровня, называемого уровнем дозаказа, то дистрибьютор включает данную позицию в заказ. Заказываемое количество является постоянной величиной, называемой количеством дозаказа. Мы делаем несколько предположений:

1) если товар заказан в конце недели, то он поступает в начале следующей;

2) если потребительский спрос в течение недели превышает запасы на начало недели, то происходит потери возможных продаж из-за того, что не отслеживается постоянно потребительский спрос;

3) потребительский спрос на определенную деталь в различные недели являются независимыми случайными переменными;

4) маргинальное распределение недельного спроса на запчасть определенного вида одинаково в каждую неделю.

Менеджер предприятия оценил возможные значения недельного спроса на запчасть и вероятности этих значений (см. файл ЗАПАС.XLS (шаблон и решение). Он хочет оценить ожидаемые доходы за первые две недели по определенному виду деталей, предполагая, что в начале первой недели их было 250. Значения уровня дозаказа и количества дозаказа предполагаются заданными (рис. 62).

Решение

Исходные данные задачи представлены на рис. 62.

Построим совместное распределение спроса по первой и второй неделе. Для этого помещаем в ячейку С21 формулу =ПРОСМОТР(C$20;РаспрТабл)* ПРОСМОТР($B21;РаспрТабл) и копируем ее в массив С21:G25. Для проверки находим суммы по столбцам и строкам (маргинальные распределения). Совпадают с Е12:Е16.

Далее вычислим ожидаемый доход в первую неделю. Для этого поместим в ячейку С30 формулу =Цена*МИН(C29;НачЗап) и скопируем ее по ряду 30.

Для вычисления ожидаемого дохода разместим в ячейке В32 формулу =СУММПРОИЗВ(Доход1;Вероятн1).

Основной лист модели представлен на рис. 63.

Теперь вычислим ожидаемый доход второй недели. Очевидно, что он зависит от результатов первой недели. Введем дополнительные обозначения:

• I — запас на начало первой недели;

• D — спрос первой недели;

• RP — уровень дозаказа.

Тогда возможен в точности один из случаев:

• если I — D ≤ 0, то запас на конец недели равен 0 и на начало следующей поступает стандартный дозаказ в размере 400;

• если 0 < I — D ≤ RP, то на начало следующей недели будет I — D + 400;

• если I — D > RP, то на начало следующей недели будет I — D.

Исходя из этих соображений, вычислим доход второй недели для всех возможных вариантов. Для этого разместим в ячейке С37 формулу =Цена*МИН($B37; ЕСЛИ(НачЗап-C$36<=0; КолДозак; ЕСЛИ(НачЗап-C$36<=УровДозак; НачЗап-C$36+КолДозак; НачЗап-C$36))) и скопируем ее в массив С37:G41. Для вычисления ожидаемого дохода второй недели разместим в ячейке В43 формулу =СУММПРОИЗВ(Доход2;СовмВер).

Теперь мы можем исследовать зависимость ожидаемых доходов от входных параметров (а не назначать их вслепую)! Для этого используем инструмент Таблица подстановки…, описанный в примере из подраздела 3.5. Однако в отличие от предыдущего примера мы используем этот инструмент для анализа зависимости доходов сразу от двух параметров — уровня дозаказа и количества дозаказа. Значения этих параметров мы размещаем в ячейках А53:А57 и B52:H52 соответственно. Полученная таблица подстановки представлена на табл. 21.

Далее, используя Мастер диаграмм, можно построить трехмерную диаграмму полученных зависимостей (рис. 64).

Следует отметить, что большинство наших примеров, в том числе и данный, не являются реальными моделями бизнеса, а являются лишь упрощенными прообразами таких моделей. Совершенно очевидно, что данная модель не учитывает ряд важных обстоятельств. Так, например, не учитывается возможный эффект уменьшения цены с ростом размера заказа, затраты, связанные со стоимостью транспортировки, хранения, замораживания определенных финансовых вложений в товаре, динамическое изменение спроса, более продолжительные периоды функционирования, риски, связанные с недопоставками или отклонениями в сроках поставок и т.д. Попытка рассмотрения моделей с учетом вышеперечисленных факторов потребовала бы привлечения дополнительного математического и программного инструментария и вывела бы нас за рамки данного учебника. Несколько более усложненные модели управления запасами будут рассмотрены в дисциплине «Моделирование и количественный анализ в менеджменте».

Под взвешенной суммой случайных величин понимается сумма данных величин умноженных на числовые множители (веса). Такие взвешенные суммы, например, часто встречаются в задачах из сферы финансов. Определим некоторые понятия. Пусть X₁ , X₂ ,…,X_n  — случайные величины (зависимые или независимые), а a₁ , a₂ ,…,a_n  — константы. Тогда новая случайная величина Y записывается следующим образом:

Y = a₁ X₁ + a₂ X₂ + … + a_n X_n .

Математическое ожидание вычисляется как:

Дисперсия в случае независимых случайных величин определяется из соотношения:

Дисперсия в случае зависимых случайных величин определяется как:

Пример

Инвестор предполагает инвестировать 100 000 руб. в портфель из восьми акций. Имеется накопленная информация о значениях обобщающих характеристик — математические ожидания доходностей, стандартные отклонения и матрица парных корреляций отдельно по всем видам акций (см. файл ПОРТФЕЛЬ ИНВЕСТОРА.XLS (шаблон и решение). Рассчитаем обобщающие характеристики портфеля, указанного в строке 9 (рис. 65).

Решение

В данной задаче в качестве весов берутся количества денег, инвестируемые в акции данного вида, а в качестве случайной величины рассматривается доход с одного доллара, вложенного в акции данного вида.

Рассчитываем математическое ожидание доходности портфеля в ячейке В49 по формуле =СУММПРОИЗВ(Веса; Средние) (рис. 65).

Для расчета дисперсии необходимо учесть, что:

Удобно первоначально создать колонку стандартных отклонений, используя функцию ТРАНСП (TRANSPOSE). Для этого выделим ячейки H49:H56, введем формулу =ТРАНСП(СтОткл) и одновременно нажмем клавиши Ctrl + Shift + Enter.

Далее построим таблицу вариаций и ковариаций. Для этого введем в ячейку В28 формулу =$H49*B$13*B17 и скопируем ее в массив В28:I35. По диагонали массива стоят вариации.

И, наконец, вычислим дисперсию доходности портфеля в ячейке В50. Выполним ряд шагов.

Сформируем ряд весов. В ячейку В38 поместим формулу =Веса, выделим массив В38:I38 и нажмем одновременно комбинацию клавиш Ctrl + Shift + Enter.

Сформируем колонку весов. В ячейку А39 поместим формулу =ТРАНСП(Веса) и нажмем одновременно комбинацию клавиш Ctrl + Shift + Enter.

Сформируем таблицу элементов. В ячейку В39 введем формулу =$A39*B28*B$38 и скопируем ее по массиву В39:I46.

Вычислим дисперсию и стандартное отклонение. Введем в ячейку В50 формулу =СУММ(Элементы), а в ячейку В51 введем корень квадратный из этой величины.

Результаты вычислений представлены на рис. 66.

Можно вводить различные структуры портфеля и исследовать зависимость между уровнем доходности и риском. В частности, используя методы оптимизации, которые будут представлены в разделе 3, можно решать следующие задачи.

Задача 1. Определить структуру портфеля, обеспечивающую максимально возможную ожидаемую доходность, при заданном ограничении на степень риска (ограничение сверху на стандартное отклонение ожидаемой доходности).

Задача 2. Определить структуру портфеля, обладающего минимальной степенью риска (минимальное значение стандартного отклонения ожидаемой доходности) и обеспечивающую ожидаемую доходность не ниже заданной.

В данной теме мы познакомились с основными понятиями теории вероятностей (вероятностная независимость, условная вероятность, совместная вероятность, аддитивное и мультипликативное правило теории вероятностей) и обобщенными характеристиками случайных величин (математическое ожидание, дисперсия, стандартное отклонение). Мы также рассмотрели примеры простейших вероятностных моделей, охватывающие наиболее часто встречаемые случаи: распределение сценарного типа, совместная вероятность, независимые случайные величины. Как было показано в вышеприведенных примерах, данные модели, построенные на основе вероятностной информации, позволяют производить количественный анализ эффективности принимаемых решений.