На практике часто возникает необходимость определить некоторые характеристики больших совокупностей. Например, процент людей, использующих определенную пасту для чистки зубов. Однако невозможно опросить всех. Возникает понятие случайной выборки. Освоив материал данной теме, вы узнаете:

• каковы методы построения таких случайных выборок;

• как по свойствам выборок можно делать утверждение относительно характеристик всей совокупности.

Генеральная совокупность — множество всех элементов рассматриваемой совокупности. Элемент выборки — элемент совокупности, отобранный в выборку. Размер выборки — количество элементов выборки. Вероятностные выборки — построенные на основе некоторого случайного механизма. Субъективные выборки — построенные по субъективным правилам лица, строящего выборку.

Будем заниматься вероятностными выборками, так как иные не подчиняются статистическим законам, и точность полученных на их основе результатов слабо поддается количественной оценке.

В этой теме обсуждаются конкретные методы построения выборок, применяемые на практике. Часто существует некоторый баланс, между сложностью построения и качеством выборки.

Главный принцип простейшего подхода — это равновероятность всех возможных выборок. Пусть N — количество элементов во всей совокупности, а n — размер выборки. Если эти значения малы и количество этих выборок невелико, то теоретически можно разбить интервал от 0 до1 на N равных подынтервалов, каждый из которых соответствовал бы одному из элементов исходной совокупности, и воспользоваться случайной функцией СЛЧИС (RAND), которая генерирует значения случайной величины, равномерно распределенной на интервале (0; 1). Обращаясь к данной функции n раз, мы бы выбирали элементы, соответствующие тем подынтервалам, куда попадали бы случайные числа. Однако существует и другой более рациональный подход. Рассмотрим пример.

Пример

Рассмотрим файл СЛУЧАЙНАЯ ВЫБОРКА.XLS, (шаблон и решение), который содержит данные о доходах 40 семей. Мы хотим построить случайную выборку размера 10. Как это сделать? Как соотносятся обобщающие характеристики выборки и всей совокупности?

Решение

Можно применить наиболее простой способ — метод простых случайных выборок. Сгенерируем вспомогательный столбец, содержащий случайные числа, которые можно получить с помощью функции СЛЧИС(). Далее произведем сортировку рядов в соответствии с величиной полученных случайных чисел. В качестве искомой выборки возьмем первые десять клиентов после сортировки (рис. 89). Конкретнее выполним следующие процедуры:

• введем функцию =СЛЧИС() в ячейку С10 и скопируем ее по столбцу;

• далее «зафиксируем» массив случайных чисел, выделив его с помощью команд Правка/Копировать и Правка/Специальная вставка с опцией «значения»;

• скопируем массив А10:С49 в массив E10:G49;

• выберем массив E10:G49 и произведем сортировку с помощью меню Данные/Сортировка по полю Случайное Число;

• в качестве случайной выборки выберем 10 верхних значений в ячейках F10:F19;

• далее в рядах 5 и 6 с помощью функций СРЗНАЧ (AVERAGE), МЕДИАНА (MEDIAN) и СТАНДОТКЛОН (STDEV) вычислим эти характеристики по всей совокупности и по выборке.

Для того чтобы повторить эту процедуру многократно с различными выборками, может быть написан макрос. Смотрите следующий лист в файле СЛУЧАЙНАЯ ВЫБОРКА.XLS, (шаблон и решение), где создана специальная кнопка для повторных генераций выборок.

Средства, реализованные в StatPro, позволяют строить выборки заданного размера указанное количество раз. Смотрите StatPro/Statistical Inference/Generate Random Samples.

Пример

Имеются данные о 280 счетах, выставленных клиентам компании «Промкомплект» (cм. файл СЧЕТА.XLS (шаблон и решение), которые содержат следующую информацию:

1) категория клиента (крупный, средний, мелкий);

2) количество дней с момента выставления счета;

3) размер счета.

Необходимо сгенерировать 50 случайных выборок размера 15 только из мелких покупателей, вычислить средний размер их счетов и построить гистограмму полученных 50 результатов.

Решение

Можно применить возможности, содержащиеся в надстройке StatPro.

Сначала добавим новый столбец А, в котором введем нумерацию всех элементов совокупности от 1 до 280. Отделим данные о мелких клиентах, вставив пустую строку. Далее пройдем по следующим позициям меню StatPro/Statistical Inference/Generate Random Samples... Зададим в качестве параметров 50 и 15, а в качестве места размещения результатов новый лист Выборки. Эта процедура выдает индексы тех элементов множества, которые включаются в выборку.

Для того чтобы получить величины задолженностей для выбранных счетов введем функцию =ПРОСМОТР(Выборки!B3;Данные!$A$4:$A$153;Данные!$D$4:$D$153) в ячейку В20 и скопируем ее в массив В20:AY34.

Далее можно воспользоваться специальной функцией вычисление средних СРЗНАЧ в ряде 37.

Преобразуем 37 строку в столбец, выделив ячейки ВА3:ВА52, введя формулу =ТРАНСП (B37:AY3) и нажав одновременно клавиши Ctrl + Shift + Enter (рис. 90).

Воспользуемся средствами построения гистограмм, содержащимися в StatPro, для отображения средних значений, полученных по 50 выборкам (рис. 91).

Приведем лишь общую идею метода. Делим общее количество элементов в совокупности на размер выборки. Получаем размер блока. Далее случайным образом получаем позицию в этом блоке. От нее с интервалом, равным размеру блока, выбираем элементы. Иногда этот метод может приводить к непредставительным выборкам (пример с днями недели).

Рассмотрим данный метод, который также иногда называют методом пропорциональных частичных выборок. Предположим, что все множество исходных данных, состоящее из N элементов, разбито на I непересекающихся подмножеств, состоящих из N_i элементов, так что:

N = N₁ + N₂ + … + N_i

Для того чтобы получить выборку размера n, нам необходимо выбрать n_i представителей из каждой i-й подгруппы так, чтобы:

n = n₁ + n₂ + … + n_i .

Количества n_i вычисляют, округляя величины n • N_i / N. После того как величины n_i определены, мы можем применить метод простых случайных выборок, описанный в примере для выбора представителей в каждой подгруппе.

Данный способ определения количества выбираемых элементов в каждом подмножестве имеет тот недостаток, что не учитывает разницу в стандартных отклонениях в различных подмножествах. Существует формула, оптимизирующая эти размеры в зависимости от величин стандартных отклонений.

Пример

Фирма, занимающаяся обслуживанием кредитных карточек определенного типа, располагает информацией о 1000 своих клиентах (см. файл СТРАТИФИКАЦИЯ.XLS (шаблон и решение). Она планирует провести более тщательные маркетинговые исследования рынка кредитных карт в целом, а именно оценить средний объем использования кредитных карт других типов. Фирма приняла решение исследовать круг клиентов исходя из их принадлежности к той или иной возрастной группе. В качестве размера общей выборки решено взять количество 100. А далее произвести телефонный опрос этой группы.

Решение

В первую очередь фирма, справедливо полагая, что люди разного возраста имеют разные склонности и разное отношение к кредитным картам, приняла решение о выделении возрастных групп. После предварительных исследований, было решено выделить следующие категории: 18—30, 31—62, 63—80 (среди клиентов не было никого моложе 18 или старше 80). Далее вся необходимая информация вносится в таблицу Excel, а именно: размер выборки, верхние и нижние границы возрастных групп и информация по клиентам.

Используя логические функции Excel, производим разбивку на возрастные группы. А именно введем функцию =ЕСЛИ (B11<=$D$6;1;ЕСЛИ (B11<=$D$7;2;3) в ячейку С11 и скопируем ее в колонке С.

Произведем операцию расстыковки данных (unstuck) по признаку возрастной категории, используя StatPro/Data Utilities/Unstack Variables. В качестве кодовой переменной необходимо указать переменную Группа.

Используя функцию СЧЕТ (COUNT), подсчитаем количество клиентов в каждой возрастной группе. А именно введем формулу =СЧЕТ (Е11:Е142) в ячейку F6 и аналогичные в ячейки F7 и F8.

Вычислим количество выбираемых элементов в каждой подгруппе, используя функцию округления ОКРУГЛ (ROUND). Для этого введем формулу =ОКРУГЛ (РазмВыборки*F6/1000;0) в ячейку G6 и аналогичные в ячейки G7 и G8 (рис. 92).

Зная размеры выборок для каждой категории, применяем метод простых случайных выборок (рис. 93).

Основная идея подхода состоит в разбиении исходной совокупности на подмножества, выборе некоторых из этих подмножеств случайным образом и включении в итоговую выборку всех представителей выбранных подмножеств.

Схема, описанная выше, называется одношаговой. На практике применяются также многошаговые схемы, предполагающие разбиение исходного множества на категории, подкатегории и т.д. и проведение случайных выборок на каждом уровне.

Целью построения выборок является оценка некоторых параметров всей совокупности. В этом разделе обсудим математические процедуры таких оценок. Будем исходить из метода простых случайных выборок, хотя общие идеи для других способов аналогичны.

Ошибки делятся на два основных класса — ошибки выборки и прочие ошибки.

Ошибки выборки происходят в том случае, если случайным образом мы получили некоторую специфическую выборку (не из-за наших неправильных действий).

Прочие ошибки могут быть вызваны различными причинами:

• уклонением от ответа: не можем определить, имеет ли группа не ответивших существенные отличия от группы ответивших;

• недостоверными ответами: часто вызывается поставленными вопросами (на некоторые из них человек всегда хочет сказать «нет»);

• ошибками измерения: например, несовпадением ответа и того, что хотел узнать спрашивающий.

Ошибки такого рода плохо поддаются количественной оценке.

Ошибку измерения математического ожидания можно выразить как:

Можно ли каким-то образом оценивать величину этой ошибки? Ответ на этот вопрос основывается на знании закона распределения выборочного математического ожидания. Справедливы следующие соотношения:

Поскольку стандартное отклонение всей совокупности нам не известно (σ), вместо него используется его оценка s.

Приближение

Пример

Аудитор хочет оценить среднюю сумму счета, выписываемого компанией ее клиентам. Поскольку компания располагает 10 000 счетами, аудитор делает выборку размером 100 (см. файл АУДИТ.XLS (шаблон и решение). Какой вывод можно сделать из этой информации?

Решение

Вычисляем выборочное математическое ожидание и выборочное стандартное отклонение в ячейках В7 и В8 по формулам =СРЗНАЧ(Суммы) и =СТАНДОТКЛОН(Суммы).

Далее вычисляем оценку для стандартного отклонения среднего (см. формулу выше) =СтОткл/КОРЕНЬ(РазмерВыб) (рис. 94).

Таким образом, вспомнив правила интервалов, можно утверждать, что с вероятностью 95% истинное среднее значение суммы счета находится в диапазоне от 279 руб. — 2 • 42 руб. = 195 руб. до 279 руб. + 2 • 42 руб. = 363 руб.

В предыдущем примере использовали правила областей именно потому, что справедлива следующая теорема (которая является некоторой модификацией центральной предельной теоремы теории вероятностей).

Теорема: Для любой случайной величины X с математическим ожиданием μ и стандартным отклонением σ случайная величина 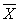имеет примерно нормальное распределение с математическим ожиданием μ и стандартным отклонением 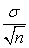. Чем больше n, тем лучше приближение.

В более общем виде центральная предельная теорема показывает, почему нормальное распределение имеет особую роль в математической статистике. Оказывается, что усреднение независимых случайных величин (необязательно одинаково распределенных!) близко к нормальному распределению.

Размер выборки может определяться исходя из финансовых и временных ограничений.

Он также определяется из соображения желаемой точности результата. Если предполагаемую максимальную абсолютную ошибку обозначить за В, то можно утверждать следующее: если размер выборки есть

,

то с вероятностью 95% абсолютная величина ошибки измерения математического ожидания не превзойдет В.

1. Для оценки математического ожидания совокупности используем выборочную оценку n₁ (среднее значение).

2. Точность оценки определяется стандартным отклонением ее распределения, которое может быть оценено по формуле 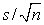, где s есть стандартное отклонение выборки.

3. По центральной предельной теореме оценка n₁ имеет примерно нормальное распределение при больших n, что позволяет использовать правила областей.

4. С ростом n точность оценки возрастает. Есть формула для расчета величины выборки при заданном уровне точности.

В этой главе мы познакомились с методами построения случайных выборок, методами оценки математического ожидания. Получили некоторые соотношения для оценки точности выборочного среднего.
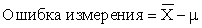
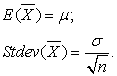
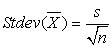
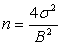