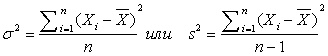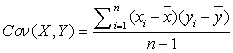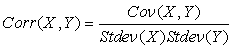Понять смысл каждой из обобщающих характеристик числовой совокупности. Уметь вычислять обобщающие характеристики, как с помощью функций Excel, так и с помощью средств надстройки Анализ данных. Уметь использовать обобщающие характеристики для проверки различных гипотез.

Основная идея всех инструментов анализа данных, представленных в теме 1, была концентрация данных. Мы тем или иным способом группировали данные, а затем отображали их в виде таблиц, графиков или диаграмм. Иногда нужно обобщить их еще больше, до конкретных значений, которые называются обобщающими характеристиками.

В данной теме мы рассмотрим основные обобщающие характеристики одной переменной и обобщающие показатели, характеризующие взаимосвязь между двумя переменными.

Среднее значение — это усредненное значение по всем имеющимся данным. В Excel имеется специальная функция для вычисления среднего значения СРЗНАЧ (AVERAGE). Вычислительная формула для выборки из n значений приведена ниже.

Среднее значение является оценкой для математического ожидания случайной величины, определение которого будет рассмотрено в разделе 2. Там же будет дано пояснение понятию статистической оценки.

Пример

В файле ЗАРПЛАТЫ.XLS (шаблон и решение) имеются данные о зарплатах 190 выпускников некоторой бизнес — школы. Вычислим среднее значение.

Решение

Применяем функцию СРЗНАЧ (AVERAGE), вызывая ее через Мастер функций. В табл. 9 приведены результаты вычисления и других обобщающих характеристик, которые будут рассмотрены далее.

Медиана — это среднее значение среди совокупности значений упорядоченных в порядке возрастания. Медиана делит совокупность значений на две части таким образом, что слева и справа от медианы находится одинаковое количество значений. Если количество значений нечетное, то медиана совпадает со средним по количеству значением (сколько слева, столько и справа), а если четное, то медиана является серединой между двумя средними по количеству значениями.

Пример

Вычислить медиану в предыдущем примере о зарплатах выпускников (см. файл ЗАРПЛАТЫ.XLS (шаблон и решение).

Решение

Используем функцию МЕДИАНА (MEDIAN). Результат можно увидеть в табл. 9.

Замечание. Важно понимать разницу между средним значением и медианой. Обе характеристики являются своего рода серединами совокупности значений, однако первая из них является серединой по значениям, а вторая серединой по количеству значений.

Мода — это наиболее вероятное значение. Это характеристика имеет смысл для дискретных распределений, то есть распределений случайной величины, принимающей конечное число возможных значений.

Пример

Файл РАЗМЕРЫ.XLS (шаблон и решение) содержит данные о размерах мужских костюмов, приобретаемых в универмаге. Какой размер пользуется наибольшей популярностью?

Решение

Используем функцию МОДА (MODE). Наиболее распространенными размерами костюмов являются 50 и 51. Аналогичный результат можно было бы получить и с помощью гистограммы, приведенной на рис. 21 (подумайте как?).

Медиана определяет середину (по количеству точек) совокупности. Однако часто возникает необходимость найти другие разбиения, например, такое, что левее границы разбиения находится 90% значений, а правее 10%. Подобные задачи можно решать с помощью функций ПЕРСЕНТИЛЬ (PERSENTILE) и КВАРТИЛЬ (QUARTILE), которые располагаются в разделе «статистические» мастера функций Excel.

Пример

Необходимо вычислить уровень зарплаты (см. файл ЗАРПЛАТЫ.XLS (шаблон и решение), ниже которого получают только 5% выпускников и уровень зарплаты, ниже которого получают 95% выпускников.

Решение

Используем функцию ПЕРСЕНТИЛЬ, а именно вычислим значения функций =ПЕРСЕНТИЛЬ (Зарплата; 0,05) и =ПЕРСЕНТИЛЬ (Зарплата; 0,95), которые равны соответственно 23 690 и 35 810. Следовательно, справедливы следующие утверждения:

• 5% выпускников получают зарплату менее 23 690 долл. в год;

• 5% выпускников получают зарплату выше 35 810 долл. в год.

Пример

Необходимо вычислить уровень зарплаты (см. файл ЗАРПЛАТЫ.XLS (шаблон и решение)), ниже которого получают только (?) выпускников и уровень зарплаты, ниже которого получают (?) выпускников.

Решение

Используем функцию КВАРТИЛЬ, а именно вычислим значения функций =КВАРТИЛЬ (Зарплата; 1) и =КВАРТИЛЬ (Зарплата; 3), которые равны соответственно 27 325 и 32 300. Следовательно, справедливы следующие утверждения:

• 25% выпускников получают зарплату менее 27 325 долл. в год;

• 25% выпускников получают зарплату выше 32 300 долл. в год.

Замечание. Разница между значениями предыдущей задачи, а именно суммарная ширина двух средних квартилей, в которых находится половина значений, называется межквартильным расстоянием и часто обозначается IQR (interquartile range).

Эти величины находятся с помощью встроенных функций МИН (MIN), МАКС (MAX) и разности их значений.

Пример

Необходимо вычислить максимальный и минимальный уровень зарплаты (см. файл ЗАРПЛАТЫ.XLS (шаблон и решение) выпускников.

Решение

Используем функции МАКС и МИН, а именно вычислим =МАКС(Зарплата) и =МИН(Зарплата), где Зарплата — имя области данных, содержащей значения зарплат. Соответствующие значения функций будут 38 200 и 17 100 долл. в год.

Разбросом значений называется разница между максимальным и минимальным значениями. В данном примере он равен 38 200 — 17 100 = 21 100.

Очень важно знать не только положение «центра» совокупности значений, но и меру их разброса вокруг этого «центра». Мерой такого разброса в статистике являются дисперсия и стандартное отклонение. Дисперсия есть среднеожидаемый квадрат отклонения случайной величины от своего среднего значения (математического ожидания). Стандартное отклонение определяется как корень квадратный из дисперсии.

Ниже приведены две основные формулы для выборочной дисперсии:

Существование нескольких формул для определения дисперсии связано с существованием нескольких оценок для дисперсии. Это обстоятельство объясняет наличие нескольких функций для вычисления дисперсии в библиотеке функций Excel. Понятие оценки нами будет раскрыто в разделе II.

Пример

Предположим, что некоторая фирма приняла решение прекратить выпуск подъемных рельсов, а приобретать их у поставщиков. Фирме требуются рельсы диаметром в 1 дм. Компания получила образцы в количестве 10 штук от двух поставщиков. Результаты их замеров приведены в файле ИЗМЕРЕНИЯ 4.XLS (шаблон и решение). Кого из поставщиков следует предпочесть?

Решение

Заметим, что все три характеристики — среднее значение, медиана и мода для обоих поставщиков одинаковы и равны 1 дм. Однако кроме этого, необходимо вычислить меру разброса значений. Для этого необходимо вычислить такие статистические характеристики, как дисперсию и стандартное отклонение, а точнее, их выборочные аналоги. Это можно сделать с помощью функций ДИСП (VAR) и СТАНДОТКЛОН (STDEV). Результаты применения статистических функций приведены на рис. 22.

Интерпретация стандартного отклонения: правила областей.

Многие распределения имеют симметричную форму, а графики их функций плотности распределения имеют колоколообразную форму (нормальное распределение). Тогда стандартное отклонение можно интерпретировать следующим образом (правила областей):

• примерно 68% наблюдений находятся в радиусе одного стандартного отклонения от среднего значения;

• примерно 95% наблюдений находятся в радиусе двух стандартных отклонений от среднего значения;

• примерно 99,7% (то есть почти все) наблюдений находятся в радиусе трех стандартных отклонений от среднего значения.

Эти правила на следующем примере.

Пример

В файле ИНДЕКС.XLS (шаблон и решение) приведены значения индекса Доу Джонса по завершению каждого месяца за период с 1947 по 1993, а также ежемесячные изменения индекса, выраженное в процентах. Насколько соответствуют этим данным правила областей, приведенные выше?

Решение

Построим графики временных рядов для ежемесячных значений индекса (рис. 23) и его ежемесячных процентных изменений (рис. 24).

Далее осуществим следующие процедуры:

• вычислим среднее значение и стандартное отклонение для величин доходностей;

• вычислим границы интересующих нас интервалов;

• вычислим распределение частот по этим интервалам с помощью функции ЧАСТОТА (FREQUENCY).

Замечание. При использовании данной функции выход из мастера функций осуществляется одновременным нажатием клавиш Ctrl + Shift + Enter.

Выразим эти частоты в процентах и сравним с частотами, указанными в правилах областей (рис. 25).

Как мы видим, полученные результаты хорошо согласуются с показателями правил областей.

Помимо встроенных функций СРЗНАЧ (AVERAGE), ДИСП (VAR), СТАНДОТКЛОН (STDEV), МАКС (MAX), МИН (MIN) и так далее можно использовать так же базовое средство Excel «Анализ данных» и расширение StatPro. Приведем пример использования расширения StatPro.

Пример

Обратимся вновь к данным файла ЗАРПЛАТЫ.XLS (шаблон и решение). Вычислим основные характеристики выборки.

Решение

Проведем следующие процедуры:

• поместим курсор в область данных;

• выберем StatPro/Summary Stats/One -Variables Summary Stats;

• выберем интересующие нас переменные (обобщающие показатели будут вычисляться для каждой из них);

• выберем интересующие нас обобщающие показатели в специальном диалоговом окне (некоторые вычисляются по умолчанию) рис. 26);

• определим область отображения результатов.

Ниже приведены результаты, представляемые StatPro (табл. 10).

Аналогичные возможности получения совокупности обобщающих показателей имеются и в Пакете анализа Excel — Сервис/Анализ данных…/Описательная статистика.

До этого мы рассматривали характеристики одной случайной величины. Ковариация и корреляция — величины, которые оценивают меру наличия линейной взаимосвязи двух случайных величин. Для вычисления выборочных значений этих величин необходимо иметь некоторый набор спаренных данных. Выражение для выборочной ковариации:

В Excel существует специальная функция, реализующая данную формулу — КОВАР (COVAR). Знак этой величины показывает характер зависимости, а именно если рост одной из величин, как правило, влечет за собой рост другой, то знак ковариации положительный, если же с ростом одной из величин другая уменьшается, то знак ковариации отрицательный.

Недостатком является то, что ковариация зависит от единиц измерения величин. В отличие от ковариации коэффициент корреляции не зависит от единиц измерения величин. Выражение для выборочного коэффициента корреляции выражается формулой:

В Excel существует специальная функция, реализующая данную формулу — КОРЕЛ (CORREL). Знак этой величины имеет тот же смысл, что и в случае ковариации. Коэффициент корреляции всегда изменяется в границах от -1 до 1. Для независимых случайных величин коэффициент равен 0. Коэффициент корреляции равен 1 тогда и только тогда, когда переменные связаны строго линейной зависимостью с положительным коэффициентом и равен -1, если коэффициент линейной зависимости отрицательный.

Пример

В файле ЗАРПЛАТЫ.XLS (шаблон и решение) приведены данные опросов 100 семей по поводу структуры их финансовых затрат, а именно, имеются данные об их зарплатах, затратах на культурные мероприятия, спортивные мероприятия, питание в общественных местах за прошедший год. Наблюдается ли между этими характеристиками какая-либо линейная зависимость?

Решение

Можно построить диаграммы рассеивания для каждой пары (потребуется 6 графиков). Быстрее получить таблицу парных корреляций с помощью StatPro, а именно StatPro/Summary Stats/Correlations (Covariances) (табл. 11).

Построим диаграммы рассеивания для тех пар переменных, для которых коэффициент корреляции существенно отличается от 0, а именно: Рестораны — Доход (рис. 27) и Досуг — Спорт (рис. 28).

Это средство может использоваться как для графического отображения распределения одной переменной, так и для сравнения распределения двух и более переменных.

Пример

Обратимся вновь к файлу ИНДЕКС.XLS (шаблон и решение), в котором собранны данные об изменении индекса Доу Джонса за период с февраля 1947 г. по январь 1993 г. Используйте прямоугольную диаграмму для отображения распределения изменений индекса.

Решение

Эта возможность имеется в расширении StatPro. Диаграмма может быть построена с использованием StatPro/Charts/Boxplot. Основные моменты для понимания диаграммы следующие:

• справа и слева от квадрата находятся третий и первый квартили. Таким образом, квадрат заключает в себе средние 50% наблюдений, а его ширина равна IQR;

• вертикальная линия внутри квадрата показывает положение медианы;

• точка внутри квадрата показывает положение среднего значения;

• горизонтальные линии слева и справа от квадрата достигают крайних наблюдений, которые отстоят от границ квадрата не более чем на 1,5 ширины квадрата (IQR). Они показывают степень разброса значений, а также направление скоса;

• остальные наблюдения показаны точками. Если они находятся на удалении от 1,5IQR до 3IQR, то называются средними выбросами и не закрашиваются, иначе они называются экстремальными выбросами и закрашиваются.

Графическое изображение прямоугольной диаграммы, а также численные значения, связанные с ней, приведены на рис. 29.

Сопутствующая количественная информация отображается в специальной таблице (табл. 12). Таким образом, инструмент прямоугольные диаграммы сочетает в себе, как визуальный образ выборки значений, так и набор количественных характеристик.

Пример

Обратимся вновь к файлу АКТЕРЫ.XLS (шаблон м решение). Используем совместно построенные прямоугольные диаграммы для отображения распределения зарплат мужчин и женщин и их сравнения.

Решение

Поскольку данные по мужчинам и женщинам приведены в едином массиве, необходимо использовать опцию stacked (состыкованы). Если бы мы имели два отдельные массива для гонораров мужчин и гонораров женщин, то использовалась бы опция unstacked (расстыкованы). Таким образом, строим прямоугольную диаграмму с помощью StatPro/Charts/Boxplot, используя переменную Пол, как кодовую, а переменную Гонорары, как измеряемую. На рис. 30 приведена соответствующая пара прямоугольных диаграмм.

Видно, что прямоугольник диаграммы, построенной для женщин, находится левее, чем построенный для мужчин, хотя они имеют примерно одинаковую ширину (IQR). Это означает, что наиболее близкие к среднему гонорары женщин меньше средних гонораров мужчин. Аналогичное соотношение хорошо видно для средних значений и медиан. Выбросы отсутствуют, что говорит о том, что соотношение средних гонораров не результат отдельных низких гонораров женщин или отдельных очень больших гонораров мужчин, а скорее общее правило.

В этом разделе мы опробуем инструменты на некоторых более сложных и объемных данных, хотя и эти данные, по крайней мере, по своим объемам, далеки от реальных. Пока цель наших действий извлечь информацию из имеющихся данных — это первый шаг на пути бизнес-анализа и принятия решений. Необходимо ясно понимать, что приведенные ниже способы анализа данных являются не жестко предопределенными, а всего лишь возможными. Желательно в каждом случае самостоятельно провести какие-либо уточняющие исследования.

Пример

Компания «Промкомплект» производит и реализует широкий ассортимент производственных товаров. Благодаря их разнообразию имеется большое количество потребителей. Их можно разделить на мелких, средних и крупных в зависимости от объемов совместного с компанией «Промкомплект» бизнеса. В последнее время наметилась проблема с оплатой счетов. Это естественно приводит к финансовым потерям. Если, например, компания-потребитель не оплачивает задолженность в размере 300 руб. в течение 20 дней, то «Промкомплект» теряет недополученный процент с капитала. Компания располагает данными по 280 счетам, в которых указана категория потребителя, размер долга, количество дней просрочки оплаты (см. файл СЧЕТА.XLS (шаблон и решение). Какую информацию можно извлечь из имеющихся данных?

Решение

Для того чтобы составить первоначальное представление о данных, рассчитаем основные обобщающие характеристики переменных (табл. 13), далее построим гистограмму распределения по суммам задолженности (рис. 31) и двумерную диаграмму рассеивания по дням и суммам (рис. 32).

Обратите внимание на две группы точек на диаграмме рассеивания. Одна из них не имеет видимого порядка, другая же имеет более ярко выраженную положительную тенденцию. Природа наблюдаемого явления будет выяснена нами в ходе дальнейших исследований.

Следующим логическим шагом было бы использовать разбиение клиентов по категориям и провести исследования данных по каждой категории с использованием известных программных инструментов, а именно для каждой категории отдельно:

• вычислить основные статистические характеристики (табл. 14);

• построить гистограммы по суммам задолженностей (рис. 33, 34, 35);

• построить сравнительные (по категориям) прямоугольные диаграммы по количеству дней просрочки (рис. 36);

• построить сравнительные (по категориям) прямоугольные диаграммы по суммам задолженностей (рис. 37);

• построить диаграммы рассеивания по «дням» и «суммам» (рис. 38, 39, 40).

Разбиение (расстыковка) данных для дальнейшего анализа можно осуществить, например, с помощью StatPro/Data Utilities/Unstack Variables…, указав в качестве кодовой переменной поле Категория.

На данном этапе мы уже можем сделать некоторые выводы, а именно:

• крупных потребителей намного меньше, чем средних и мелких;

• суммы долгов крупных клиентов значительно больше чем мелких;

• мелкие потребители, как правило, не настолько задерживают выплаты как средние и крупные;

• не наблюдается зависимости между суммой долга и количеством дней просрочки для мелких потребителей, в то время как для средних и крупных просматривается положительная зависимость.

Далее допустим, что компания хочет отделить покупателей, которые должны менее 500 долл. Результаты можно получить, введя некоторую новую категорию Размер, которая есть 0, если клиент имеет задолженность менее 500 долл. и 1, в противном случае. Для построения можно использовать условный оператор. В данном случае выражение = ЕСЛИ (C6>=$B$3;1;0) помещается в ячейку D6 и далее копируется вниз по столбцу.

Используя возможности сводных таблиц, исследуем распределение «больших» и «малых» задолженностей по категориям клиентов. С этой целью ниже приведены три сводные таблицы — для распределения по количеству счетов (табл. 15), процентное распределение по столбцам (табл. 16) и по строкам (табл. 17).

Данные таблицы характеризуют распределение мелких и крупных счетов по категориям клиентов с точки зрения их количества. Интересным представляется исследовать распределение суммарных задолженностей по мелким и крупным счетам и по категориям клиентов. Результаты такого анализа представляют следующие три сводные таблицы (табл. 18—20).

И, наконец, мы хотели бы исследовать вопрос об оценке финансовых потерь, возникающих из-за задержек платежей. Исходим из 12% ставки годового дохода, которая является параметром и размещается в ячейке D7. Вычислим потери по каждой из категорий, введя переменные — потери по просроченным счетам для категорий — Потери1, Потери2, Потери3. Ниже приведен фрагмент расчетной таблицы потерь. Типичной формулой расчета, например, формулой из ячейки C10 является =В10*A10*$D$7/365.

Далее подсчитываются суммарные потери по всем трем категориям (рис. 41).

В заключение отобразим полученные результаты по суммарным потерям в категориях в виде круговой диаграммы (рис. 42).

Полученная информация дает определенную картину того, как реально в компании обстоит дело с задолженностями клиентов и является основой для принятия последующих решений. Используя функцию текущей даты, можно сделать вышеприведенную расчетную модель динамической и построить систему мониторинга суммарной задолженности, распределения задолженностей, потерь от просроченных платежей и других параметров.

Рассмотрим еще один пример анализа данных.

Пример

Супермаркет «Москва» открыт 24 ч. в сутки, 7 дн. в неделю. В последнее время увеличилось количество нареканий со стороны посетителей в связи с долгим ожиданием кассового обслуживания. Компания «Москва» приняла решение разобраться с данной ситуацией, предварительно собрав данные о времени прибытия клиентов к кассовым очередям, завершения их обслуживания и длинам очередей к кассам. Данные собирались с интервалом в 30 мин. в течение всей недели, начиная с 8 утра понедельника до 8 утра понедельника следующей недели — всего 336 наблюдений. В ходе обследования собирались данные четырех типов, а именно:

• количество покупателей, находящихся в кассовых очередях в начале данного периода (Ожидавшие первоначально);

• количество покупателей подошедших к кассам в данный период (Прибывшие);

• количество покупателей, завершивших процесс обслуживания в данный период (Обслуженные);

• количество касс, работающих в течение данного периода (Кассы).

Данные собраны в файле ОБСЛУЖИВАНИЕ.XLS (шаблон и решение). Данные также содержат временные характеристики, а именно:

• день недели (День);

• время начала каждого периода (Начальное время);

• названия определенных периодов дня (Период): Утренний пик (6.00—9.00), Утро (9.00—11.30), Предобеденый пик (11.30—13.30), День (13.30—16.30), Дневной пик (16.30—18.30, Вечер (18.30—23.00), Ночь (23.00—6.00).

Кроме этого, в данных содержится некоторая вычисляемая переменная, а именно количество покупателей, находящихся в очереди на конец данного периода (Оставшиеся). Как нетрудно заметить, Оставшиеся = Ожидавшие первоначально + Прибывшие — Обслуженные. Фрагмент данных приведен на рис. 43.

Менеджер компании намеревается проанализировать имеющиеся данные и выявить определенные тенденции наблюдаемых показателей в зависимости от времени дня и дня недели. Кроме этого, он планирует оценить обоснованность алгоритма, по которым открываются и закрываются кассы супермаркета в течение дня. Конечно, ему хотелось бы найти «наилучший» алгоритм открытия и закрытия касс, но эта задача в данный момент нами не рассматривается.

Решение

Поскольку в данной ситуации время является весьма существенным фактором, имеет смысл начать исследование с построения временных рядов некоторых показателей. На рис. 44 изображены временные ряды для переменных Ожидавшие первоначально (нижняя линия) и переменной Прибывшие (верхняя линия), построенные за недельный период. На экране монитора они выделены различными цветами. Анализируя данные временные ряды можно прийти к следующим выводам:

• наиболее загруженными днями являются пятница и суббота (наиболее высокие участки графика по переменной Прибывшие;

• графики переменой Прибывшие в будние дни и в выходные несколько различаются, во втором случае он более широкий;

• в будние дни довольно четко выделяются пиковые периоды прихода покупателей, а в выходные дни приход более равномерный в течение дня.

На рис. 45 изображены временные ряды для переменных Прибывшие и Обслуженные. Трудно различить графики данных временных рядов. Это означает, что в основном магазин обслуживает столько покупателей, сколько их приходит.

Для дальнейших исследований целесообразно использовать сводные таблицы, сочетая их для наглядности с графическим изображением. Фрагмент одной из таких сводных таблиц с соответствующим графическим изображением представлен на рис. 46.

Для создания данной сводной таблицы, мы размещаем переменную Ожидавшие первоначально в области Элементы данных, выбирая при этом опцию представления данных Среднее значение, переменную Начальное время размещаем в области Поля строк, а переменную День указываем в области Поля страниц. Используя возможность группировки, мы могли бы рассмотреть более агрегированные временные интервалы (попробуйте самостоятельно). Кроме этого, используя информацию из сводной таблицы, мы строим временной ряд, показывающий среднюю длину кассовых очередей в течение суток. Используя опцию Поля страниц, мы имеем возможность просмотреть данный временной ряд для каждого дня недели и сравнить их.

Аналогичным образом создаем сводную таблицу для исследования среднего количества покупателей, прибывающих в течение получаса в различные временные периоды суток. Для этого переменную Прибывшие помещаем а область Элементы данных, выбирая при этом опцию представления данных Среднее значение, переменную Период размещаем в области Поля строк, а переменную Дни указываем в области Поля страниц. Используя данные из сводной таблицы, строится соответствующая гистограмма для каждого дня недели. Как и в предыдущем случае, используя опцию Поля страниц, мы получаем возможность просмотреть данный временной ряд для каждого дня недели и сравнить их. Результаты сводной таблицы и гистограмма для пятницы приведены на рис. 47 и 48 соответственно.

Для того чтобы периоды в сводной таблице следовали в хронологическом порядке необходимо предварительно сформировать соответствующий список в программе Excel, используя Сервис/Параметры/Список.

Можно заметить, что гистограмма для пятницы несколько отличается от гистограмм для других рабочих дней недели.

Менеджер компании хочет оценить «правильность» того количества касс, которые работают в магазине в течение суток в различные дни недели. Для прояснения данного вопроса построим диаграмму рассеивания между количеством касс (Кассы) и переменной Всего = Ожидавшие первоначально + Прибывшие. Эта переменная показывает объем имеющейся работы для касс в каждые полчаса. Данная диаграмма рассеивания показана на рис. 49. Как мы видим, между этими величинами просматривается сильная положительная зависимость. Это говорит о том, что менеджер действует в целом правильно, когда увеличивается нагрузка на кассы, менеджер увеличивает их количество.

Далее рассмотрим диаграмму рассеивания для переменных Кассы и Оставшиеся. Данная диаграмма изображена на рис. 50.

Как и в предыдущем случае, просматривается явная положительная зависимость, то есть периоды, на начало которых в очередях остается много людей, как правило, имеют большое количество работающих касс. Однако в этом случае мы видим, что хотя менеджер в целом, верно, реагирует на рост очередей, однако эта реакция недостаточная.

Возникает желание, внося изменения в количество открытых касс, добиться лучшей их связи с рассмотренными показателями. Однако здесь необходимо учитывать, по крайней мере, два обстоятельства.

Во-первых, изменение параметра Кассы повлечет изменение параметров Обслуженные, Ожидавшие первоначально, Оставшиеся. Эти изменения достаточно сложны для оценки (математическая теория очередей).

Во-вторых, увеличение количества открытых касс влечет за собой дополнительные расходы кассиров, а следовательно, менеджер должен решать задачу выбора между дополнительными расходами на оплату работы кассиров и потерями, которые вызывают длинные очереди. Эта задача весьма сложная.

Рассмотренный нами инструментарий, состоящий из встроенных функций Excel и возможностей расширения StatPro, позволяет извлекать первичную информацию, «спрятанную» в данных за считанные минуты.

1. Morris С. Quantitative Approach in Business Studies / Clare Morris. — Pitman.

2. Бююль А. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей / А. Бююль, П. Цефель. — СПб.: ООО «ДиаСофтЮП», 2002. — 608 с.

3. Дюк В. Data Mining: учеб. курс / В. Дюк, А. Самойленко. — СПб.: Питер, 2001. — 367с.

4. Сигел Э. Практическая бизнес-статистика / Эндрю Сигел. — М.: Вильямс, 2002. — 1056 с.

5. Символоков Л.В. Решение бизнес-задач в Microsoft Office / Л.В. Символоков. — М.: БИНОМ, 2001. — 512 с.