Локальная и интегральная теоремы Лапласа

 

Пусть производится n одинаковых независимых испытаний с вероятностью появления события в каждом испытании, равной p. Тогда вероятность частоты m наступления события А определяется, как было показано ранее, по формуле Бернулли:

.

Вычисление по этой формуле трудно практически осуществить при n>20.

Муавром и Лапласом была получена асимптотическая формула, позволяющая найти указанную вероятность. Теорема, выражающая эту формулу, носит название локальной теоремы Муавра-Лапласа.

Если производится n одинаковых испытаний, в каждом из которых вероятность появления события равна p, то вероятность того, что данное событие появится m раз, определяется по формуле:

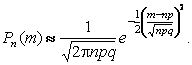
Эта теорема дает приближение биномиального закона распределения к нормальному при n ®¥  и p, значительно отличающемся от нуля и единицы. Для практических расчетов удобнее представлять полученную формулу в виде:

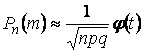,    ;    .         (1.9)

 

Если m=m₀=np, то вероятность наиболее вероятной частоты находится по формуле:

 

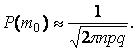
Пример 1.10. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

        

Решение. По условию n = 400, p = 0,75 , q = 0,25 и m = 280, откуда

 

.

 

По таблицам j(t) найдем j(-2.31)= j(2.31) = 0,0277.

Искомая вероятность равна:

 

 

Для вычисления вероятности того, что частота m, подчиненная биномиальному закону распределения, заключена между данными значениями m₁ и m₂, применяют интегральную теорему Лапласа, выраженную асимптотической формулой:

 

где

 

Формулу, выражающую интегральную терему Лапласа, можно получить из закона нормального распределения (см. далее), положив

X = m;  x₁=m₁;  x₂=m₂;  m = np; 

При больших значениях n наиболее вероятная частота m₀ совпадает с математическим ожиданием (см. далее) частоты. Поэтому для нахождения вероятности того, что абсолютная величина отклонения частоты от наиболее вероятной частоты не превосходит заданного числа e > 0, применим формулу закона нормального распределения

P(|X-m|<ts) = Ф(t),

где X = m; m = M(m) = m₀; ;  ts = e.

Заметим, что, пользуясь теоремами Лапласа, можно находить вероятность того, что частость  примет заданное значение.

 

 

К оглавлению

Назад к разделу "Повторение испытаний. Формула Бернулли"

Вперед к разделу "Формула Пуассона"