Определение ожидаемой доходности и дисперсии портфеля

 

         Ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле

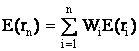          (13)

где W_i - вес каждой ценной бумаги в портфеле. Подставим в эту формулу выражение для r_i из формулы (12):

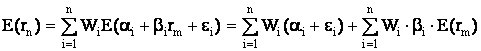       (14)

 

Для придания этой формуле компактности, Шарп предложил считать рыночный индекс как характеристику условной (n+1)-ой ценной бумаги в портфеле. В таком случае, второе слагаемое уравнения  (14)можно представить в виде:

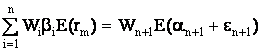     (15)

 

где: 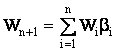;    (15a)

        .

 

при этом считается, что дисперсия (n+1)-ой ошибки равна дисперсии рыночной доходности: . Выражение (15a) представляет собой сумму взвешенных величин “беты” (b_i) каждой ценной бумаги (где весом служат W_i) и называется портфельной бетой (b_n). С учетом выражений (14) и (15) формулу (13) можно записать так:

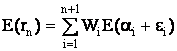                     (16)

 

а поскольку E(e_i) = 0, то окончательно имеем:

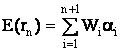                                (17)

         Итак, ожидаемую доходность портфеля E(r_n) можно представить состоящей из двух частей:

         а) суммы взвешенных параметров a_i каждой ценной бумаги –
W₁a₁ + W₂a₂ + .... + W_na_n, что отражает вклад в E(r_n) самих ценных бумаг, и

         б) компоненты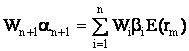, то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.

 

 

К оглавлению

Назад к разделу "Оптимизация инвестиционного портфеля по методу Шарпа"

Вперед к разделу "Дисперсия портфеля"