Дисперсия портфеля в модели Шарпа представляется в виде:
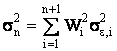 (18)
(18)
При
этом только необходимо иметь в виду, что 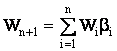 то есть (Wn+1)2=(W1b1 + W2b2 + .... + Wnbn)2, а
то есть (Wn+1)2=(W1b1 + W2b2 + .... + Wnbn)2, а ![]() . Значит, дисперсию портфеля, содержащего n ценных бумаг,
можно представить состоящей из двух компонент:
. Значит, дисперсию портфеля, содержащего n ценных бумаг,
можно представить состоящей из двух компонент:
а)
средневзвешенных дисперсий ошибок 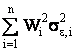 , где весами служат Wi,
что отражает долю риска портфеля, связанного с риском самих ценных бумаг
(собственный риск)
, где весами служат Wi,
что отражает долю риска портфеля, связанного с риском самих ценных бумаг
(собственный риск)
б) ![]() - взвешенной величины дисперсии рыночного показателя
- взвешенной величины дисперсии рыночного показателя![]() , где весом служит квадрат портфельной беты, что отражает долю риска портфеля, определяемого
нестабильностью самого рынка (рыночный риск)
, где весом служит квадрат портфельной беты, что отражает долю риска портфеля, определяемого
нестабильностью самого рынка (рыночный риск)
В модели Шарпа цель инвестора сводится к следующему:
необходимо найти минимальное значение дисперсии портфеля
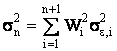 (19)
(19)
при следующих начальных условиях:
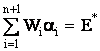 (20)
(20)
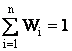 (21)
(21)
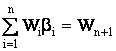 (22)
(22)
Итак, отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:
1) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности ri,t каждой ценной бумаги.
2) По рыночному индексу (например, AK&M) вычислить рыночные доходности rm,t для того же промежутка времени.
3)
Определить величину дисперсии рыночного показателя ![]() , а также значения ковариаций si,m доходностей каждой ценной
бумаги с рыночной нормой отдачи и найти величины bi:
, а также значения ковариаций si,m доходностей каждой ценной
бумаги с рыночной нормой отдачи и найти величины bi:
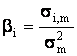
4) Найти ожидаемые доходности каждой ценной бумаги E(ri) и рыночной доходности E(rm) и вычислить параметр ai:
ai = E(ri) - biE(rm)
5) Вычислить дисперсии σ2ε, і ошибок регрессионной модели
6) Подставить эти значения в соответствующие уравнения
После такой подстановки выяснится, что неизвестными величинами являются веса Wi ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля E*, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.
Назад к разделу "Определение ожидаемой доходности и дисперсии портфеля"