§ 4.2. Динамическое программирование

 

Динамическое программирование есть особый метод оптимизации решений, специально приспособленный к так называемым «многошаговым», или «многоэтапным» операциям.

 

§ 4.2.1 Постановка задачи

 

Представим себе некоторую операцию , распадающуюся на ряд последовательных шагов, - например, деятельность предприятия в течении нескольких хозяйственных лет; поэтапное планирование инвестиций; управление производственными мощностями в течение длительного срока; или же преодоление группой самолетов нескольких полос противовоздушной обороны; или же распределения весов многоступенчатой ракеты между ее ступенями с целью оптимизации скорости. Некоторые операции расчленяются на шаги естественно; в некоторых членение приходится вводить искусственно – скажем, процесс наведения ракеты на цель можно условно разбить на этапы, каждый из которых занимает какое-то время .

Рассмотрим управляемый процесс. Предположим, что управление можно разбить на  шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему из начального состояния в конечное, представляет собой совокупность  пошаговых управлений. В результате управления система переходит из состояния  в .

Обозначим через  управление на ом шаге (к = 1, 2, ..., n).  – множество допустимых управлений на ом шаге.

Пусть  – управление, переводящее систему из состояние  в состояние . Обозначим через  состояние системы после ого шага управления. Получаем последовательность состояний . (рисунок 18).

 

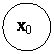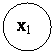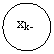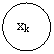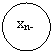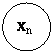            u₁          u₂ ..... u_k-1          u_k             u_k+1 .. u_n-1            u_n

 

Рис. 18 Переход системы из одного состояния в другое в результате управляющих сигналов

Показатель эффективности рассматриваемой управляемой операции зависит от начального состояния и управления:

                                                                        (1)

 - множество возможных управлений

Сделаем несколько предположений:

1. Состояние  системы на ом шаге зависит только от предшествующего состояния  и управления на ом шаге  и не зависит от предшествующих состояний и управлений (свойство отсутствия последействия):

   уравнения состояний            (2)

 - оператор перехода

2. Целевая функция (1) является аддитивной от показателя эффективности каждого шага, т.е. выигрыш за всю операцию складывается из выигрышей на отдельных шагах.

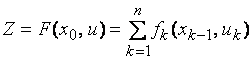                                            (3)

 показатель эффективности шага                  (4)

 

Общая постановка задачи ДП. Определить такое допустимое управление , переводящее систему из состояния  в состояние , при котором целевая функция (3) принимает максимальное значение.

 

 

К оглавлению

Назад к разделу "§ 4.1. Отличительные черты подхода исследования операций"

Вперед к разделу "§ 4.2.2. Принцип решения задач динамического программирования"