8.4. Циклические группы. Группы подстановок

 

Пусть G —группа, HиF— ее подгруппы. Тогда пересечение D=H∩Fнепустое, поскольку оно содержит единичный элемент. Dтакже является подгруппой группы G. Действительно, если элементы а и bпринадлежат D, то их произведение и обратные им элементы содержатся как в H, так и в F, и поэтому также принадлежат D. Аналогично доказывается и следующее утверждение.

Теорема. Пересечение любого множества подгрупп группы G само является подгруппой этой группы.

Пусть S — произвольное непустое подмножество группы G. Рассмотрим всевозможные подгруппы G, которые содержат S в качестве подмножества. Одной из них будет, в частности, сама группа G. В силу теоремы пересечение всех таких подгрупп будет подгруппой G, которая называется подгруппой, порожденноймножеством S, и обозначается <S>.

Если множество S состоит из одного элемента а, то порожденная им подгруппа <a> называется циклической подгруппой, порожденной элементом а.

Обозначим (a^-1)^k=a^-k.

Теорема. Циклическая подгруппа <а>, порожденная элементом а, состоит из всех степеней элемента а.

Заметим, что все степени элемента а принадлежат подгруппе <а> и для любого целого k (a^-1)^-k=a^k. С другой стороны, эти степени сами составляют подгруппу, так как a^maⁿ=a^m+n, a°=e, а обратным элементу а^п является элемент а^-n. Действительно, нетрудно доказать, что для любых целых mи п

a^maⁿ=a^m+n ; (а^т)^п=а^тп.

 

Для натуральных т и п это следует из свойств операций. Если m<0, n<0, то

a^maⁿ =(a^–1) ^–m(a^–1)^-n=(a^–1)^-(m+n)= a^m+n

Если m<0, n>0, то

a^maⁿ =(a^–1)^-maⁿ=(a^-1…a^-1)(a…a)=

                                           -m раз      n раз

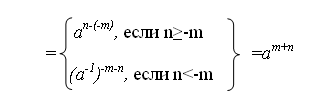
Случай m>0, n>0 аналогичен предыдущему. Доказательство второго равенства предлагается провести самостоятельно.

Группа, совпадающая с одной из своих циклических подгрупп
(т. е. состоящая из степеней одного из своих элементов), называется  циклической, а  элемент, из  степеней которого состоит циклическая группа,— ее образующим. Всякая циклическая группа коммутативна.

Пример.

1.  Группа (Z, +, 0) — циклическая. Ее образующий элемент — число 1. Это бесконечная группа. В качестве ее образующего можно взять число 1.

2.  Рассмотрим множество квадратных матриц второго порядка с целыми элементами и определителем, равным 1. Это группа относительно операции умножения матриц (покажите сами). Тогда матрица А = порождает бесконечную циклическую подгруппу, при

этом Aⁿ=.

3.   

Теорема. Всякая подгруппа циклической группы сама циклическая.

Действительно, пусть G = <a>—циклическая группа с образующим элементом а и Н — подгруппа G, отличная от единичной. Предположим, что положительная наименьшая степень элемента а, содержащаяся в H, есть a^k. Тогда < a^k > H. Допустим, что в Н содержится элемент а^l, где l≠0 и l не делится на k. Тогда, если d— наибольший общий делитель чисел kи l, существуют такие целые числа и и v, что ku+lv=d, и, следовательно, в H должен содержаться элемент (a^k)^u(a^l)^v=a^d. Но так как d<.k, то приходим к противоречию относительно выбора элемента a^k. Следовательно, H=<a^k>.

Пусть G — произвольная группа, a — некоторый ее элемент. Если все степени элемента а различны, то говорят, что элемент а имеет бесконечный порядок. Если для некоторых т и п, где т≠п, а^т=а^п, то
a^\m-n\=е, т. е. существуют положительные степени элемента а, равные единичному элементу. Пусть q— наименьшее положительное число, для которого а^q=е. Тогда говорят, что a — элемент конечного порядка q.

Рассмотрим еще один важный класс групп.

Пусть X—-конечное множество из n элементов. Группа всех биекций множества Xвсебя называется симметрической группой степени п. Без ограничения общности можно считать, что множество Xсостоит из элементов {1, 2, ..., n}. Каждая биекция :ХХ называется подстановкой и записывается символом 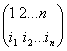, где под элементом k, 1kn, записан его образ . Произведением подстановок является композиция отображений . Например, для подстановок

 и  имеем . В то же время , так что . Единичную (тождественную) подстановку обозначаем е=. Симметрическая группа степени п обозначается S_nи содержит n! элементов.

Пример. Группа S₃состоит из следующих шести элементов:

 

a₁=e=, a₂=, a₃=, a₄=, a₅=, a₆=

 

Для подстановки имеем

 

, =e.

 

Тогда (2) =4, ² (2) =5,  (2) =2.

В подстановке  элементы 1 и 3 остаются на месте, элемент 2 переходит в 4, элемент 4 — в 5, а элемент 5 — снова в 2. Такая подстановка называется циклом (245) длины 3. Этот же цикл можно записать и так: (452), (524).

В общем случае подстановка , перемещающая элементы j₁, j₂,…,j_k так, что (т. е. где k — наименьшее число, обладающее этим свойством), и оставляющая на месте остальные элементы, называется циклом длины kи обозначается (j₁,…,j_k). Циклы называются независимыми, если любые два из них не имеют общих переставляемых элементов.

 

Теорема. Каждая подстановка в S_n является произведением независимых циклов. Разложение подстановки в произведение циклов длины 2 определено однозначно с точностью до порядка циклов.

Два элемента i и j множества Xназываются эквивалентными относительно подстановки , если j= для некоторого целого числа s. Введенное отношение есть отношение эквивалентности на множестве X. Оно разбивает множество Xна классы эквивалентности по этому отношению:. Каждый элемент iпринадлежит одному и только одному классу X_l, причеммножество X_lсостоит из образов элемента i при действии степеней подстановки  где k_l – количество элементов в X_l. Множество X_lчасто называют . В каждом классе эквивалентности X_rвыберем по одному представителю i_rи подставим ему в соответствие цикл  соответствующей длины k_r. Любой элемент, не принадлежащий X_r, остается на месте при действии степеней . Тогда подстановка  есть произведение циклов

 

                                                                            (8.4.1.)

Замечание. Если цикл  имеет длину 1, то он действует как тождественная подстановка, Такие циклы в записи можно опускать, например:

 

=(156)(38)(47)(2)=(156)(38)(47).

 

Докажем единственность. Пусть

                                                                            (8.4.2.)

есть разложение, отличное от 8.4.1; i― символ, не остающийся на месте при действии подстановки . Тогда для одного и только одного цикла  из разложения (8.4.1) и для одного и только одного цикла из разложения (8.4.2) . Для каждого k =0, 1, 2, ... имеем . Поскольку цикл однозначно определяется действием подстановки на символ i, не остающийся на месте, то . Аналогично доказываются совпадения и остальных циклов разложений (8.4.1) и (8.4.2).

Цикл длины 2 называется транспозицией. Любой циклможно записать в виде произведения транспозиций, например:

 

(1 2...t-1 t)=(1 t)(1 t-1)...(1 3)(1 2).

 

Тогда из теоремы вытекает

Следствие. Каждая подстановка в S_nявляется произведением транспозиций.

Пример. В группе S₄ (123)=(13) (12)=(23) (13)=(13) (24) (12) (14).

Разложение в произведение транспозиций не является единственным.

Можно доказать, что если — разложение  в произведение транспозиций, то число.=(-1)^k, называемое четностью подстановки , не зависит от способа разложения и

                                                                              (8.4.3)

для любых двух подстановок  и .

Подстановка  называется четной, если , и нечетной, если . Все транспозиции – нечетные подстановки.

Множество четных подстановок степени n образуют подгруппу A_n, которая называется знакопеременной. Действительно, согласно (8.4.3),  поскольку  Множество нечетных подстановок не образует группу, так как произведение двух нечетных подстановок есть четная подстановка.

 

К оглавлению

Назад к разделу "8.3. Группы: определение и примеры"

Вперед к разделу "8.5. Кольца: определение, свойства, примеры"