Поиск
отрезка, содержащего точку максимума. Алгоритм Свенна
Исходные
данные. х0 - начальная
точка, h - шаг поиска (h>0).
Шаг 1. Вычислить f(x0); f(x0+h); f(x0-h); k=1.
Шаг 2. Если f(x0-h) 
f(x0) f(x0+h), то
x1 =
x0
+ h, перейти к шагу 4.
Шаг 3. Если f(x0-h) 
f(x0) f(x0+h),
то х1 = x0-h, h = -h, перейти к шагу 4, в
противном случае (f(x0-h) f(x0) f(x0+h)) a = x0 – h; b = x0 + h, конец.
Шаг 4. xk+1
= xk + 2kh ,
вычислить f(xk+1).
Шаг 5. Если f(xk+1) f(xk),
то к = к + 1, перейти к шагу 4.
Шаг 6. Если h >
0, то a = xk-1 , b = xk+1 , конец, в противном случае
a = xk+1 , b = xk-1 , конец.
Заметим,
что случай f(x0-h) f(x0) f(x0+h)
(шаг 3) не рассматривается, так как он противоречит
предположению об унимодальности функции f(x).
Уменьшение
длины отрезка, содержащего точку максимума, достигается путем последовательного
исключения частей этого отрезка. Величина интервала, исключаемого на каждом
шаге, зависит от расположения двух пробных точек внутри отрезка. Поскольку
координата точки максимума априори неизвестна, целесообразно размещать пробные
точки таким образом, чтобы обеспечивать уменьшение длины отрезка в одном и том
же отношении.
Дихотомический поиск (метод
деления отрезка пополам)
Пробные
точки y, z на каждом шаге этого метода выбираются следующим
образом:
где δ – параметр
метода, 0 < δ < (b-a).
При малых δ каждая из
пробных точек делит отрезок почти пополам, т.е. исключению будет подлежать
почти половина отрезка.
Алгоритм.
Исходные данные. Отрезок [a; b],
содержащий точку максимума; параметр δ и параметр окончания счета
ε (ε > 2δ).
Шаг 1. a1 = a ; b1 = b ; k = 1.
Шаг 2. Если bk – ak < ε , 
, конец.
Шаг 3. 
;
A = f(y)
; B = f(z).
Шаг 4. Если A > B, то ak+1
= ak ; bk+1 = z; в противном случае ak+1=y; bk+1 =
bk
Шаг 5.
k = k+1, прейти к шагу 2.
На каждой итерации дихотомического
поиска производятся два вычисления значения функции и после n
вычислений (n/2 итераций) длина начального интервала уменьшается
приблизительно в 2n/2 раз.
Метод золотого сечения
Как
известно, золотым сечением отрезка называется деление отрезка на две неравные
части так, чтобы отношение длины всего отрезка к длине большей части равнялось
отношению длины большей части к длине меньшей части отрезка. Легко доказать,
что золотое сечение отрезка [a; b] производится двумя точками
y и z, симметричными относительно середины отрезка.
λ Δ
λ
Δ (λ – 1)Δ
y z
a b
(λ – 1)Δ Δ
Отсюда
y =
(λ – 1)a + (λ – 1)2b = 0,618 a + 0,382 b.
z =
(λ – 1)2a + (λ – 1)b = 0,382 a + 0,618 b.
Нетрудно также проверить, что точка y
производит золотое сечение отрезка [a; z], а точка z
производит золотое сечение отрезка [y;b]. На этом свойстве,
позволяющем на каждой итерации вычислить значение функции лишь в одной пробной
точке, и основан алгоритм метода золотого сечения.
Исходные
данные: [a; b] – отрезок, содержащий
точку максимума; ε – параметр окончания счета.
Шаг 1. 
; k = 1 ;
ak = a ; bk
= b ;
y = (λ – 1)ak + (λ
– 1)2bk ; A = f (y);
z = (λ – 1)2ak
+ (λ – 1)bk ; B = f
(z).
Шаг 2. Если A
> B, то перейти к шагу 4.
Шаг 3. ak+1 = y ; bk+1 = bk ;
y = z ; A = B ;
z = (λ – 1)2ak+1
+ (λ – 1)bk+1 ;
B = f (z),
перейти к шагу 5.
Шаг 4. ak+1 = ak
; bk+1 = z ; z = y ; B = A ;
y = (λ – 1)ak+1 +
(λ – 1)2bk+1 ;
A = f
(y).
Шаг 5. Если bk+1 – ak+1 < ε , то
конец.
Шаг 6. k = k + 1, прейти к шагу 2.
Как
было отмечено выше, на каждой итерации метода золотого сечения производится
лишь одно вычисление значения функции. При этом длина полученного в результате
одной итерации отрезка составит
(λ–1)Δ, где Δ –
длина исходного интервала.
Если
сравнить методы дихотомического поиска и золотого сечения, используя в качестве
критерия эффективности 
- относительное уменьшение
интервала после n вычислений значений функции f (х), где Δn
–длина интервала, полученного после n вычислений, то
т.е. метод золотого сечения оказывается более
эффективным.
Метод средней точки
Для
отыскания корня уравнения
f / (х) = 0,
которому соответствует точка максимума унимодальной
и дифференцируемой на заданном отрезке функции f (х), будем пользоваться алгоритмом исключения интервалов, на каждой
итерации которого рассматривается лишь одна точка z.
Если в
точке z выполняется условие
f / (z) > 0,
то с учетом предположения об унимодальности можно
утверждать, что точка максимума не может находиться левее точки z,
следовательно, интервал x ≤ z может быть исключен. С другой стороны, если f / (z) < 0, то точка максимума
не может находиться правее точки z, т.е. исключению подлежит
интервал x ≥ z. На этих рассуждениях и
основан метод средней точки (поиск Больцано).
Алгоритм.
Исходные
данные. Точки a и b такие, что f / (а) > 0, f / (b) > 0, ε –
параметр окончания счета.
Шаг 1. 
Вычислить f / (z).
Шаг 2. Если 
то х* ≈ z, конец.
Шаг 3. Если f / (z) > 0, то a = z, перейти к шагу 1. В
противном случае b=z , перейти к шагу 1.
Метод хорд (секущих)
При
реализации этого метода учитывается не только знак производной, но и ее
значение. Метод заключается в решении уравнения
f / (x) = 0
методом хорд и носит поэтому те же название.
Предполагаем,
как и в предыдущем разделе, что знаки производной унимодальной функции f (x) на
концах отрезка [a; b] различны: f / (a) >
0 ; f / (b) <
0.
f /(x)
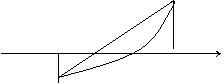
a Z X* b x
Тогда приближение z к стационарной точке х* определится по
формуле:
(13)
Алгоритм
метода хорд тот же, что и алгоритм метода средней точки за исключением того,
что координата точки z вычисляется по формуле
(13).
Метод
Ньютона-Рафсона
Предполагаем,
что унимодальная функция f(x)
дважды непрерывно дифференцируема. Тогда для решения уравнения f’(x)=0
можно применить метод касательных (Ньютона)
(14)
Алгоритм
Исходные данные. x0- начальная оценка
координаты стационарной точки, ξ – параметр окончания счета.
Шаг 1. k=0.
Шаг 2. 
.
Шаг 3. Если 
,
то 
,
конец.
Шаг 4. k=k+1, перейти к шагу 2.
Последовательность
(14) сходится к стационарной точке лишь при выполнении определенных условий,
накладываемых на вид функции и выбор начальной точки (теорема о сходимости
метода касательных).
Типовые задачи
Задача
6. Определить отрезок, содержащий точку максимума функции 
Решение.
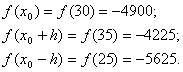
Поскольку
x*>30, x1=35.
Далее
x2=x1+2h=35+10=45.
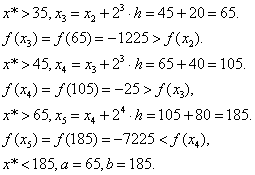
Задача 7. Найти точку
максимума функции f(x)=sin(x) на отрезке [1,5;1,6]
методом дихотомическиого поиска. δ=0,01;ε=0,035.
Решение.
Итерация 1.
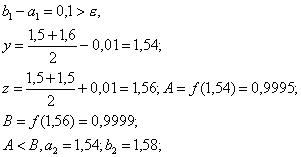
Итерация 2.
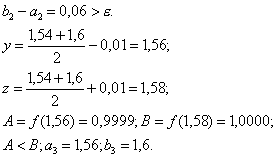
Итерация 3.
y =
1,57; z = 1,59; A = 1,000; B = 0,9998;
A
> B; a4 = a3 = 1,56; b4 = 1,59.
Итерация 4.
b4 – a4 = 0,03 < e; x* Î [1,56; 1,59].
Задача 8. Найти точку
максимума функции f(x) = sin x на
отрезке [1,5; 1,6] методом золотого сечения, e = 0,02.
Решение. l= 1,6180; a1 = 1,5; b1 = 1,6.
y = 0,6180 × 1,5 + 0,3820 × 1,6
= 1,5382.
z = 0,3820 × 1,5 + 0,6180 × 1,6
= 1,5618.
A = sin y = 0,99947; B = sin z = 0,99996.
Итерация 1. Так как A < B, то a2=y=1,5382; b2=b1=1,6.
y=z=1,5618; A=B=0,99996;
z = 0,3820 × 1,5382 + 0,6180 × 1,6
= 1,5764;
B = sin z = 0,999984;
b2 – a2 = 0,0618 > e.
Итерация 2. Так как A < B, то a3=y=1,5618; b3=b2=1,6.
y=z=1,5764; A=B=0,99998;
z = 0,3820 × 1,5618 + 0,6180 × 1,6
= 1,5854;
B = sin z = 0,99989;
b3 – a3 = 0,0382 > e.
Итерация 3. Так как A
> B, то a4=a3=1,5618; b4=z=1,5854.
z=y=1,5764; B=A=0,99998;
y = 0,6180 × 1,5618 + 0,3820 ×
1,5854 = 1,5708;
A = 1,00000;
b4
– a4 = 0,0236 > e.
Итерация 4. Так как A > B, то a5=a4=1,5618; b5=z=1,5764.
z=y=1,5708; B=A=1,00000;
y = 0,6180 × 1,5618 + 0,3820 ×
1,5764 = 1,5674;
A = sin y=0,99999;
b5 – a5 = 0,0146 < e, следовательно,
x* Î [1,5618; 1,5764].
Задача
9. Найти точку максимума функции f(x) = –2x2 – 16/x на
отрезке [1; 5] методом средней точки, e = 0,1.
Решение.
f ¢ (x)= 16/x2 – 4x.
Итерация 1.
;
f ¢ (3) = –10,222 < 0; b=3.
Итерация 2.
;
f ¢ (2) = –4 < 0; b=2.
Итерация 3.
;
f ¢ (1,5) = 1,111 > 0; a=1,5.
Итерация 4.
;
f ¢ (1,75) = –1,775 < 0; b=1,75.
Итерация 5.
;
f ¢ (1,625) = –0,441 < 0; b=1,625.
Итерация 6.
;
f ¢ (1,562) = 0,3036 > 0; a=1,5625.
Итерация 7.
;
f ¢ (1,594) = –0,077;
| f ¢ (1,594) | < e, x* » 1,594.
Задача
10. Найти точку максимума функции f(x) = sin x на
отрезке [1; 3] методом Ньютона-Рафсона, x0=2; e = 0,001.
Решение.
Итерация 1.
f ¢ (2)=cos 2= –0,4161; f ¢¢ (2)= –sin 2=
–0,9093;
; f ¢ (x1)=cos
1,5424= 0,0284 > e.
Итерация 2.
f ¢¢ (1,5424)= –sin
1,5424= –0,9996;
;
|f ¢ (1,5708)|=|cos
1,5708|= |–0,000015| < e;
x* = 1,5708.
Задача.
Отделить все корни уравнения f(x)=0 и вычислить 3
корня с точностью до трех знаков различными
методами (хорд, касательных, итераций).
