2.3. Исчисление высказываний

 

Построение формулы алгебры высказываний по заданной логической функции

 

         Рассмотрим задачу, обратную той, о которой шла речь в разделах III, IV - построение функции для некоторой формулы алгебры высказываний. Задана некоторая функция f(x₁, x₂, ... x_n), нужно построить для нее формулу S. Задача эта неоднозначна, существует множество равносильных между собой формул, соответствующих этой функции. Будем строить совершенную нормальную форму. При этом учтем, что полная элементарная дизъюнкция имеет единственный ноль, а полная элементарная конъюнкция - единственную единицу. Решение задачи рассмотрим на примере.

 

x	y	z	f
1	1	1	1
1	1	0	0
1	0	1	0
1	0	0	1
0	1	1	0
0	1	0	1
0	0	1	0
0	0	0	0

         Пусть задана некоторая функция трех аргументов f(1,1,1)=f(1,0,0)=f(0,1,0)=1. Это значит, что на наборах (1,1,1), (1,0,0), (0,1,0) функция принимает значение 1, а на остальных наборах - 0.

         Построим S в виде совершенной дизъюнктивной нормальной формы. Так как S не тождественно ложна, это можно сделать. СДНФ состоит из стольких слагаемых, сколько единиц содержит функция. Первому значению 1 соответствует слагаемое xyz, принимающее значение 1 при х=1, y=1, z=1. Второму значению 1 соответствует слагаемое , принимающее значение 1 при х=1, y=0, z=0. Аналогично третье слагаемое, соответствующее 1, стоящей в шестой строке таблицы f есть . Следовательно, . Итак:

1) Совершенная дизъюнктивная нормальная форма содержит столько слагаемых, сколько единиц имеет функция.

2) Эти единицы соответствуют тем наборам переменных, при которых каждое слагаемое (элементарная конъюнкция) обращается в единицу, т.е. переменным, входящим в элементарную конъюнкцию без знака отрицания, соответствует значение 1, а со знаком отрицания - 0.

         Чтобы написать СКНФ по заданной функции, нужно выбрать все значения 0, встречающиеся в ней, и рассмотреть наборы значений переменных, отвечающие этим нулям. В заданном примере таблица содержит пять нулей. Первому значению 0 отвечает сомножитель , обращающийся в 0 при х=1, y=1, z=0. Второму -  при х=1, y=0, z=1 и т.д. В результате получим

Итак:

1.   СДНФ содержит столько сомножителей, сколько нулей имеет истинностная таблица.

2.   Эти нули соответствуют тем наборам переменных, при которых каждый сомножитель (каждая элементарная сумма) обращается в 0, т.е. переменным, входящим в элементарную сумму без знака отрицания, соответствует значение 0, а со знаком отрицания - 1.

  Заметим, что используя список основных равносильных формул, полученные выражения для S упрощают, если это возможно.

 

Моделирование алгебры высказываний с помощью релейно-контактных схем

 

         Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - разомкнуты.

         Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x₁, ... x_n, а размыкающие - .

         Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных х_i, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.

         Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

 

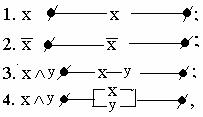
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция - последовательным.

 

 

Упражнение 2.3.1

 

         Построить функцию проводимости следующей схемы:

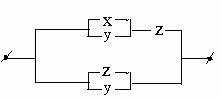
Рис. 2.3.1

 

Функция проводимости для такой схемы задается, очевидно, следующей таблицей:

                                                                                              Таблица 2.3.2

x	y	z	f(x,y,z)
1	1	1	1
1	1	0	1
1	0	1	1
1	0	0	0
0	1	1	1
0	1	0	1
0	0	1	1
0	0	0	0

 

         По данной логической функции построим формулу - СКНФ:

         Упростим это выражение: .

         Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:

Рис. 2.3.2

 

         Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить. Затем построить схему электрической цепи, моделирующую эту упрощенную формулу. Так, для электрической цепи, приведенной в данном примере,

.

 

Упражнение 2.3.2

 

         Построить наиболее простую релейно-контактную схему по заданной функции проводимости f(x,y,z): f(0,1,0)=f(1,1,0)=f(1,1,1)=0.

         Строим СКНФ: , т.к. эти сомножители обращаются в "0" на указанных наборах функции: (0,1,0), (1,1,0), (1,1,1).

         Далее упрощаем формулу S:

 

 

 

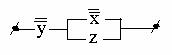
Рис. 2.3.3

 

Исчисление высказываний. Символы, формулы, аксиомы исчисления высказываний

 

         Рассмотрим формальную аксиоматическую систему, в некотором смысле адекватную алгебре высказываний. Назовем эту систему исчислением высказываний.

         Чтобы построить исчисление, нужно определить алфавит исчисления, понятие формулы, класс формул, называемых аксиомами, правила вывода данного исчисления.

         Символы исчисления высказываний состоят из знаков трех категорий:

Большие латинские буквы А, В, С, ... X, Y, Z, ..., которые назовем переменными высказываниями.

Символы операций исчисления Ù, Ú, ®, ^¾ (знак конъюнкции, дизъюнкции, следования и отрицания).

Скобки (    ).

         Других символов система исчисления высказываний не содержит.

         Формулой в исчислении высказываний является некоторая последовательность символов. Но не всякая последовательность символов есть формула. Например, последовательности А→В(С→) и (АВ) не являются формулами. Определение формулы в исчислении высказываний задается следующим образом:

1.   Всякое переменное высказывание есть формула.

2.   Если a, b есть формулы, то выражения вида (aÙb), , , (aÚb), (a®b) также являются формулами.

         Зададим в исчислении высказываний класс исходных истинных формул-аксиом.

 

Правила вывода позволяют из данной системы аксиом получать другие истинные формулы исчисления высказываний. Назовем формулу исчисления высказываний ложной, если ее отрицание истинно. Будем обозначать истинные формулы буквой R, ложные - F.

         К основным правилам вывода относятся два:

1) Правило заключения.

Если a и (a®b) - истинные формулы, то b также истинна. Это предложение можно записать в виде

2) Правило подстановки

Пусть некоторая формула a содержит переменное высказывание А. Тогда, заменив высказывание А всюду, где оно встречается, любой формулой b, получим истинную формулу. Это предложение записывается в виде

 

Формула называется выводимой в исчислении высказываний, если ее можно получить, применяя правила вывода к аксиомам исчисления высказываний. Утверждение, что формула b выводима, записывают так:

├b

 

Процесс получения формул из аксиом исчисления высказываний называется формальным выводом. Формальный вывод состоит из указания того, какие правила, в каком порядке и к каким формулам применяется для выведения данной формулы.

 

Упражнение 2.3.3

 

         Докажем, что выводима формула А®А, т.е. А®А.

1.   Запишем аксиому 2 из группы I.

(А® (В®С))®((А®В)®(А®С);

2.   Применим к ней правило подстановки , т.е.

 

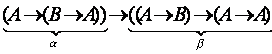
3.   Заметим, что a есть истинная формула, как аксиома из группы I, т.е. имеем истинные формулы a и a®b. Применим правило заключения  и получим (А®В)®(А®А).

4.   Применим правило подстановки к полученной формуле, заменив высказывание В на :

           .

 

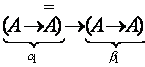5.   Но , есть аксиома 2 из группы IV. Применим к полученной формуле правило заключения , т.е. -А®А.

         Говорят, что формула b выводима из формул a₁, a₂, ..., a_n, если формулу b можно вывести путем правила заключения, приняв за исходные формулы a₁, a₂, ..., a_n и все истинные в исчислении высказываний формулы. Выводимость формулы b из формул a₁, a₂, ..., a_n записывают в виде a₁, a₂, ..., a_nb.

 

Теорема дедукции

 

         Если формула b выводима из формул a₁, a₂, ..., a_n, то выводимой является формула a₁®(a₂®(...(a_n®b)...)), т.е.

.

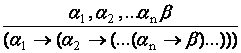         Теорема дедукции дает возможность установить выводимость различных формул исчисления высказываний более простым путем, чем непосредственный вывод этих формул из аксиом с помощью правил вывода. С помощью теоремы дедукции выводятся основные правила исчисления высказываний:

1.   Правило силлогизма. Если формулы (a®b) и (b®g) истинны, то формула (a®g), т.е. ;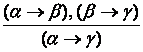

2.   Правило перестановки посылок. Если формула (a® (b®g)) истинна, то истинной является формула (b® (a®g)), т.е. ;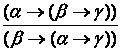

3.   Правило соединения посылок. Если истинной является формула (a®(b®g)), то истинной будет формула (aÙb®g), т.е. .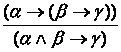

 

Проблемы непротиворечивости, полноты, независимости  аксиом исчисления высказываний

 

         Используем алгебру высказываний как некоторую модель исчисления высказываний. Формулы исчисления высказываний будем трактовать как формулы алгебры высказываний. Для этого все буквы, входящие в алфавит исчисления высказываний, будем считать переменными высказываниями в содержательном смысле, т.е. переменными, принимающими значения И и Л. Символы алфавита Ù, Ú, ®, ^¾, будем понимать как логические связки алгебры высказываний.

При этом справедлива следующая теорема.

         Все аксиомы исчисления высказываний есть тождественно истинные формулы алгебра высказываний. Все формулы, выводимые из аксиом исчисления высказываний, есть тождественно истинные формулы алгебры высказываний.

         Доказательство первой части теоремы можно провести непосредственной проверкой.

         В справедливости второй части теоремы можно убедиться, доказав, что, применяя правило заключения и правило подстановки к тождественно истинной формуле алгебры высказываний, получаем тождественно истинную формулу. Итак, всякая выводимая в исчислении высказываний формула есть тождественно истинная формула алгебры высказываний.

         При рассмотрении любой формальной логической системы, в том числе исчисления высказываний, возникает три проблемы: непротиворечивость, полнота, независимость системы аксиом исчисления.

Логическое исчисление считается непротиворечивым, если в нем не выводимы никакие две формулы, из которых одна является отрицанием другой.

         Проблема не противоречивости состоит в том, что следует выяснить, является данное исчисление непротиворечивым.

         Если в исчислении можно вывести некоторую формулу a и ее отрицание , то такое исчисление будет противоречивым. Если логическое исчисление противоречиво, в нем будет выводима любая формула. Такое исчисление не представляет ценности, т.к. оно не способно отображать в себе различие между истиной и ложью.

         Для доказательства непротиворечивости логического исчисления достаточно найти в нем хотя бы одну невыводимую формулу. В исчислении высказываний проблема непротиворечивости решается так.

         Теорема I. Исчисление высказываний непротиворечиво.

Справедливость этого утверждения следует из предыдущей теоремы. В самом деле, пусть a - некоторая выводимая в исчислении высказываний формула. Следовательно, она тождественно истинна, если ее рассматривать как содержательную формулу алгебры высказываний. Тогда  - тождественно ложна, т.е. не выводима при всех значениях входящих в нее переменных. Следовательно, a и  не могут быть вместе выводимыми в исчислении высказываний.

         Итак, любая выводимая формула в исчислении высказываний является тождественно истинной, если эту формулу исчисления высказываний рассматривать как содержательную формулу алгебры высказываний. Возникает обратная задача.

         Будет ли любая тождественно истинная формула алгебры высказываний выводима из аксиом исчисления высказываний.

         Эта задача представляет собой проблему полноты исчисления высказываний в широком смысле.

         Для любой логической системы определение полноты в широком смысле слова можно сформулировать следующим образом: логическое исчисление называется полным, если всякую истинную в содержательном смысле формулу можно вывести по правилам исчисления из аксиом исчисления.

         Для исчисления высказываний проблема полноты решается положительно.

         Теорема II. Система исчисления высказываний является полной.

         Не менее важным является определение полноты логической системы в узком смысле слова. Логическое исчисление называется полным в узком смысле слова, если добавление к системе аксиом некоторой невыводимой в этом исчислении формулы делают исчисление противоречивым. Исчисление высказываний является полным также в узком смысле слова.

         Для любой логической системы возникает проблема независимости аксиом данного исчисления. Зададимся вопросом, можно ли какую-либо аксиому исчисления вывести из остальных аксиом с помощью правил вывода данной системы. Если это возможно, то аксиому, выводимую из других аксиом, можно вычеркнуть из списка аксиом данного исчисления. Аксиома, невыводимая из остальных аксиом, называется независимой из этих аксиом. Система аксиом, в которой ни одна аксиома не выводима из остальных, называется независимой системой аксиом.

         Эта проблема для исчислений решается положительно.

 

         Теорема III. Система аксиом исчисления высказываний независима.

         Проблема независимости системы аксиом логического исчисления является весьма важной математической проблемой, приводящей иногда к вопросу о замене какой-либо аксиомы ее отрицанием. В качестве примера можно привести вопрос о независимости пятого постулата Евклида в системе аксиом геометрии, вопрос о независимости аксиомы Цермело в системе аксиом теории множеств. Вопросы эти имели большое значение в развитии математики.

 

 

К оглавлению

Назад к разделу "2.2. Проблемы разрешимости. Нормальные формы "

Вперед к разделу "2.4. Логика предикатов"