Для определения понятия предиката рассмотрим следующие примеры.
Примеры.
1. Пусть N – множество натуральных чисел, и буквой P обозначено свойство натурального числа быть простым. Если x представляет собой произвольный элемент из N, тогда выражение “натуральное число x является простым”, которое можно записать в виде P(x), уже не является высказыванием, т.к. значение истинности данного утверждения зависит от x. По существу P(x) означает переменное (неопределенное) высказывание, которое становится определенным, когда x заменено определенным элементом из N. Например, P(3) = 1, P(4) = 0. Иначе говоря, P(x) представляет собой функцию, определенную на множестве натуральных чисел и принимающую только два значения: 0 и 1.
2. Пусть Z – множество целых чисел и P – свойство пары чисел иметь одинаковый знак. Тогда P(x,y) будет означать: “целые числа x и y имеют одинаковый знак”. Это неопределенное высказывание становится определенным, если x и y заменить конкретными числами. Например, P(2,3)=1, P(-1,5)=0. Неопределенное высказывание P(x,y) представляет собой функцию двух переменных.
3. Пусть A и B – множество точек, C – множество прямых на евклидовой плоскости, а P(a,b,c) обозначает: “прямая c проходит через точки a и b”. В этом примере мы имеем дело с функцией трех переменных, причем a и b принимают значения из множества точек, а c принимает значения из множества прямых евклидовой плоскости.
Определение 1. Предикатом называется функция, отображающая множество произвольной природы во множество (0,1), или (ложно, истинно).
Обратимся теперь к определению предиката в общем случае.
Определение 2. Пусть N={N1,N2,N3,…,Nn} – конечный набор множеств. Всякая функция P(X1,…,Xn), ставящая в соответствие каждому набору из n элементов {a1,a2,…,an), где aiÎNi, какой-либо из элементов булевой алгебры (0,1) называется n-местным предикатом на N. Множество Ni называется предметной областью для переменной xi. Переменные x1,…,xnназываются предметными переменными. Некоторые из множества Ni могут совпадать.
Если при отображении P образом набора (a1,a2,…an) является единица, то записывают.
P(a1,…,an)=1
и говорят, что значение предиката P для набора (a1,…,an) является истинным. Если же образом (a1,…,an) является нуль, то записывают
P(a1,…,an)=0
и говорят, что значение предиката P для набора (a1,…,an) является ложным.
n-местный предикат при n=1 называется унарным, при n=2 – бинарным и при n=3 тернарным. Для общности введем еще понятие 0-местного предиката, а именно, 0-местным предикатом называется любе истинное или ложное высказывание.
Поскольку предикаты принимают значения из (0,1), то над ними можно производить все логические операции, рассматриваемые нами в алгебре высказываний (-, Ù, Ú, ®, «), сохраняя за ними те же определения. Кроме операций алгебры высказываний, мы будем употреблять еще две новые операции, которые связаны с особенностями предикатов и выражают собой утверждения всеобщности и существования.
Кванторы
Пусть P(x) – одноместный предикат, заданный на некотором множестве M. Если переменная x обозначает любой элемент из множества M, то P(x) является неопределенным высказыванием.
Операция " ставит в соответствие неопределенному высказыванию P(x) высказывание "xP(x), которое читается так: “для любого x имеет место P(x)” и по определению является истинным тогда и только тогда, когда P(x) истинно для любого элемента xÎM. Переход от неопределенного высказывания P(x) к высказыванию "xP(x) называется операцией навешивания квантора общности по предметному переменному x.
Операция $ ставит в соответствие неопределенному высказыванию P(x) высказывание $xP(x), которое читается так: “существует такое x, что имеет место P(x)” и по определению является истинным тогда и только тогда, когда P(x) истинно хотя бы для одного элемента xÎM. Переход от неопределенного высказывания P(x) к высказыванию $xP(x) называется операцией навешивания квантора существования по предметному переменному x.
В первом случае мы говорим, что предметная переменная x связана в предикате P(x) квантором всеобщности, во втором случае – квантором существования.
Определим операции навешивания квантора для общего случая n-местного
предиката P(x1,…,xn). Операции навешивания
кванторов " и $ по переменному x1 (в общем случае по
переменному xi, где I=![]() ) ставит в соответствие предикату P(X1,…,xn) (n-1) – местные предикаты
) ставит в соответствие предикату P(X1,…,xn) (n-1) – местные предикаты
"x1P(x1,…,xn) и $x1P(x1,…,xn)
соответственно.
Истинностные значения этих предикатов определяются для фиксированных наборов значений предметных переменных x2,…,xn следующим образом:
"x1P(x1,a2…,an)=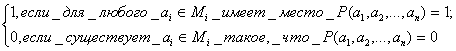
$x1P(x1,a2…,an)=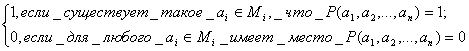
В общем случае, если k<n, то операцию навешивания квантора можно повторить k раз. Тогда переменные x1,…,xk в таком предикате будут связанными, а переменные xk+1,…,xn – свободными. При k=n предикат становится высказыванием.
Примеры.
Рассмотрим предикат Д(x1,x2) – “число x1 делится на число x2”, определенный на множестве натуральных чисел. Тогда операция навешивания кванторов приводит к следующим утверждениям:
1. "x1Д(x1,x2) – “для любого x1 имеет место Д(x1,x2)”, т.е. всякое x1 делится на x2. Этот предикат принимает значение истины только для X2=1.
2. $x1 Д(x1,x2) – “существует x1, которое делится на x2”. Этот предикат принимает значение истины для любого значения x2.
3. "x1"x2Д(x1,x2) – “для всякого x1 и для всякого x2 имеет место делимость x1 на x2. Это высказывание является ложным.
4. $x1"x2Д(x1,x2) – “существует x1, которое делится на всякое x2” – ложное высказывание.
5. "x2$x1Д(x1,x2) – “для всякого x2 существует x1 такое, что x1 делится на x2” – истинное высказывание.
Кванторы как обобщение логических связок
Пусть предметная область переменной x предикатов P(x,y) конечна: (x1,x2,…,xk). Тогда "xP(x,y) означает: P(x1,y) – истинно, P(x2,y) – истинно и т.д., т.е.
"xP(x,y) =P(x1,y)ÙP(x2,y)Ù…ÙP(xk,y).
Аналогично $xP(x,y) является сокращением дизъюнкции:
$xP(x,y) =P(x1,y)ÚP(x2,y)Ú… ÚP(xk,y).
Это показывает, что кванторы суть другая форма конъюнкции и дизъюнкции.
Отрицание кванторных предикатов
Два предиката будем считать равносильными, если их значения истинности совпадают при всех значениях входящих в них свободных переменных. При этом имеется в виду, что свободные переменные в одном предикате не являются связанными в другом.
Справедливы следующие равносильности, относящиеся к отрицаниям кванторных предикатов:
![]()
![]() .
.
Действительно, в первой из них левая часть читается: неверно, что для каждого x предикат P(x) истинен; правая – существует x, для которого P(x) ложен. Ясно, что эти два утверждения имеют один и тот же смысл. Аналогичным рассуждением убеждаемся в справедливости второй равносильности.
Таким образом, знак отрицания можно ввести под знак квантора, заменив квантор на двойственный.
Очевидно, что все равносильности, имеющие место в алгебре высказываний, переносятся и на алгебру предикатов.
Пример.
![]()
![]()
Формулы, в которых из операций алгебры высказываний имеются только операции -, Ù, Ú, а знаки отрицания относятся только к элементарным предикатам, называются приведенными формулами.