2.2. Проблемы разрешимости. Нормальные формы
Рассмотрим взаимоотношения двух высказываний P и Q:
1. Отношение следствия. Говорят, что из P следует Q, а если Q истинно всякий раз, когда истинно P; Q называют следствием P.
Пусть P и Q - сложные высказывания, составленные из элементарных высказываний A, B следующим образом Q=A®B, P=A«B.
Таблица 2.2.1
|
А |
В |
А®В=Q |
A«B=P |
|
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
В этом примере из Q не следует P, так как в третьей строке таблицы 4.1 Q принимает значение 1, в то время как P=0. Но из P следует Q, так как Q принимает значение 1 в первой и четвертой строках таблицы, т. е. тогда, когда истинно P.
Между отношением следствия и импликацией существует тесная связь. Но следует помнить, что это не одно и то же. Импликация - сложное высказывание, составленное из двух данных, а следствие - отношение между двумя высказываниями.
Таблица 2.2.2
|
P |
Q |
P®Q |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Когда импликация выражает отношение следствия? Q есть следствие P лишь при условии, что логическая возможность, соответствующая второй строке истинностной таблице 2.2.2 импликации, не должна иметь место. А в этом случае истинностная таблица импликации содержит одни единицы. Заметим, что высказывания, связанные импликацией, при отсутствии смысловой связи могут звучать парадоксально. В самом деле, высказывание “Если я не приду на лекцию, то река впадает в Белое море” звучит парадоксально. Между посылкой и заключением в этих случаях не существует отношения следствия.
Упражнение 2.2.1
Между какими парами высказывании, приведенных ниже, существует отношение следствия?
S1: Если прямая перпендикулярна радиусу окружности и проходит через точку пересечения радиуса с окружностью, то она - касательная к окружности.
S2: Прямая есть касательная к окружности тогда и только тогда, когда она перпендикулярна к радиусу окружности и проходит через точку пересечения радиуса с окружностью.
S3: Если прямая перпендикулярна к радиусу окружности, но не проходит через точку пересечения радиуса с окружностью, то она не является касательной к окружности.
S4: Если прямая проходит через точку пересечения радиуса с окружностью, но не является касательной, то прямая не перпендикулярна к радиусу окружности.
Введем элементарные высказывания:
A: Прямая перпендикулярна к радиусу окружности.
B: Прямая проходит через точку пересечения радиуса с окружностью.
C: Прямая - касательная к окружности.
Запишем формулы приведенных высказываний.
|
S1=AB®C S2=C«AB |
S3=A S4=B |
Построим истинностные таблицы этих высказываний, получим:
Таблица 2.2.3
|
А |
В |
С |
S1 |
S2 |
S3 |
S4 |
S2®S1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Из высказывания S2 следует S1 и S4, т. к. при истинностных значениях “1” в первой, четвертой, шестой и восьмой строках высказывания S2 те же значения “1” имеем в указанных строках высказываний S1 и S4 и импликации S2®S1, S2®S4 становятся тождественно истинными высказываниями S2®S1º1, S2®S4º1.
Особое место занимает пара высказываний S1 и S4. Каждая из них следует из другого: из S1 следует S4 и из S4 следует S1. В этом случае говорят, что высказывания S1 и S4 эквивалентны.
2. Отношение эквивалентности.
|
P |
Q |
P«Q |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Если истинностная таблица двойной импликации Р®Q (табл. 2.2.4.) содержит только ”1”, т. е. исключаются логические возможности, соответствующие второй и третьей строкам, значения истинности P и Q одинаковы. В этом случае говорят, что P и Q эквивалентны.
|
Таблица 2.2.4 |
Таким образом, эквивалентные высказывания задаются равносильными формулами. В упражнение 2.2.7 высказывания S1 и S4 эквивалентны.
3. Несовместимость.
Два высказывания называются несовместимыми, если не существует логической возможности, при которой оба высказывания были бы одновременно истинными, т. е. при истинном значении одного из них другое обязательно ложно.
Это понятие распространяется на любое число высказываний.
Чтобы установить совместимость высказываний, нужно построить их истинностные таблицы. Если найдется хотя бы одна строка, в которой все высказывания принимают значения “истинно”, данные высказывания будут совместимы, в противном случае - нет.
Все высказывания упражнения 2.2.1 совместимы. Примером несовместимых высказываний является пара: некоторое высказывание P и его отрицание.
Проверка правильности рассуждений
Рассуждение есть утверждение того, что некоторое высказывание (заключение) следует из других высказываний (посылок). Рассуждение считается правильным только в том случае, если из конъюнкции посылок следует заключение, т. е. между конъюнкцией посылок и заключением установлено отношение следствия. Если P1, P2, ... , Pn - посылки, а Q - заключение, то рассуждение правильно, если между высказыванием P1 Ù P2 Ù ... Ù Pn и Q установлено отношение следствия. В этом случае импликация P1 Ù P2 Ù ... Ù Pn®Q должна быть тождественно истинным высказыванием (тавтологией).
Правильность рассуждения можно установить, построив истинностную таблицу высказывания S= P1ÙP2Ù...ÙPn®Q и убедившись в том, что оно тождественно истинно.
При большом числе посылок установить тот факт, что является тавтологией, удобнее с помощью преобразований высказывания к равносильной ему формуле, являющейся тавтологией.
Метод “от противного” заключается в предположении, что заключение
ложно, и установление того факта, что при этом конъюнкция P1 Ù P2 Ù ... Ù Pn - ложна (что
имеет место в том случае, если хотя бы одна из посылок Pi (
) принимает значение “ложно”). Если это выполняется, то
рассуждение верно, в противном случае - нет. Таким образом, в случае
правильного рассуждения мы убеждаемся в том, что импликация S= P1 Ù P2 Ù ... Ù Pn®Qº1, т. к. отсутствует
логическая возможность, соответствующая P= P1 Ù P2 Ù ... Ù Pn=1, Q=0, где
импликация P®Q принимает значение ложно.
Упражнение 2.2.2
“Если функция непрерывна на данном интервале и имеет разные знаки на его концах, то внутри интервала функция обращается в нуль. Функция не обращается в нуль внутри данного интервала. но на концах интервала имеет разные знаки. Следовательно, функция разрывна”.
Посылки и заключения в данном рассуждении состоят их следующих элементарных высказываний:
A - “функция непрерывна на данном интервале”,
B - “функция имеет разные знаки на концах интервала”
C - “функция обращается в нуль внутри данного интервала”.
Используя эти обозначения, запишем посылки и заключение в виде формул:
AÙB®C (1-я посылка P1)
ÙB (2-я посылка P2)
(заключение
Q)
Если
импликация (AÙB®C)Ù(ÙB)®=P®Q тождественно истинна, то
рассуждение верно. Для проверки правильности рассуждения строим истинностную
таблицу:
|
А |
В |
С |
АВ |
АВ®С |
|
|
P1ÙP2 |
|
P1ÙP2®Q |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
Убеждаемся, что рассуждение верно. Проведем проверку правильности этого рассуждения методом от противного. Предположим, что заключение Q ложно. Покажем, что в этом случае конъюнкция посылок P1ÙP2 ложна, т. е. P →Qтождественно истинна.
В самом деле, если Q=
ложно, то A истинно.
Пусть P2=B истина, тогда B - истинно, - истинно т. е. C -
ложно, но в этом случае посылка принимает значение ложно, так как P1=АВ®С принимает значение ложно, так как AB=1, а С=0, что и
требовалось проверить.
Правильность данного рассуждения можно проверить, преобразовав формулу P1ÙP2 к некоторой равносильной ей формуле, которая задает заведомо тождественно истинное высказывание.
Это сделаем после ознакомления с так называемыми совершенными нормальными формами формул алгебры высказываний.
Нормальные формы формул алгебры высказываний
Если в какой - либо логической ситуации данная формула принимает значение “истинно”, она называется выполнимой. К классу выполнимых формул относятся такие формулы, множество истинности которых не пусто. В противном случае формула называется невыполнимой.
Установить тот факт, что данная формула является выполнимой, можно с помощью истинностных таблиц. Нужно построить истинностную таблицу данной формулы и убедиться в том, что она содержит не одни нули. В противном случае формула является невыполнимой, тождественно ложной.
При большом числе переменных истинностные таблицы громоздки. Установить тип формулы (невыполнима - тождественно ложна, выполнима – тавтология или переменное высказывание, принимающее в одних ситуациях значение “истинно”, в других - “ложно”) удобнее с помощью так называемых нормальных форм.
Определение 1. Элементарным произведением (или основной конъюнкцией) называется конъюнкция элементарных высказываний или их отрицаний.
Определение 2. Элементарной суммой (или основной дизъюнкцией) называется дизъюнкция элементарных высказываний или их отрицаний.
Элементарная конъюнкция “k” и элементарная дизъюнкция “d” над
множеством переменных 
могут быть записаны
формулами:
,
где ikÎ{1,2, ... n} для
всех 
d kÎ{0,1}, причем 
Пусть сложное высказывание состоит из 4х
элементарных, обозначенных соответственно A, B, C, D. Элементарные дизъюнкции и
элементарные конъюнкции могут быть составлены соответственно и 
элементарных
высказываний.
Так имеем K1=A
D, K2=
BC
, K3=- некоторые из элементарных
конъюнкций, соответственно d1=ÚBÚ
Ú, d2=AÚÚC - некоторые из
элементарных дизъюнкций. В дальнейшем будем пользоваться большими латинскими
буквами для обозначения переменных.
Теорема 1. Элементарное произведение является тождественно ложным тогда и только тогда, когда оно содержит пару сомножителей, один из которых является элементарным высказыванием, а другой - его отрицанием.
Теорема 2. Элементарная сумма является тождественно истинной тогда и только тогда, когда она содержит хотя бы одну пару слагаемых, из которых одно является элементарным высказыванием, а другое - его отрицанием.
Так, элементарная сумма AÚBÚCÚ тождественно истинна,
элементарное произведение ABC тождественно ложно.
Определение 3. Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных произведений, называется дизъюнктивной нормальной формой данной формулы и обозначается ДНФ.
Пример: ABCÚBÚ.
Определение 4. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных произведений, называется конъюнктивной нормальной формой данной формулы и обозначается КНФ.
Пример: (BÚÚ)(AÚB)B.
Для каждой формулы алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм. Для этого нужно:
1. Избавиться от всех логических операций, содержащихся в формуле, заменив их основными - конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
A®B=ÚB,
A«B=(ÚB)(AÚ)=ABÚ.
2. Заменить знак отрицания,
относящийся к выражениям типа 
или 
, знаками отрицания, относящимся к отдельным переменным
высказываниям на основании формул:
=Ú,
=AÙB.
3. Избавиться от знаков
двойного отрицания на основании равенства 
=A.
4. Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности.
Упражнение 2.2.3
Пусть 
. Построим КНФ для этой формулы.
1) избавимся от знаков импликации, получим:
(ÚB)«( Ú);
2) избавимся от знака двойной импликации:
;
3) избавимся от знака отрицания, относящегося к выражениям, состоящим более чем из одной переменной:
;
4) избавимся от двойных и тройных отрицаний:
;
5) применим законы дистрибутивности:
,
.
Получим S=
. Это КНФ для данной формулы S.
Используя свойства AÚA=A и AA=A, упростим КНФ для S:
S=
.
Теорема 3. Формула алгебры высказываний является тождественно истинной тогда и только тогда, когда каждый множитель ее КНФ содержит пару слагаемых, одно из которых является элементарным высказыванием, а другое - его отрицанием.
Теорема 4. Формула алгебры высказываний является тождественно ложной тогда и только тогда, когда каждое слагаемое (т. е. каждое элементарное произведение) ее ДНФ содержит пару сомножителей, один из которых есть элементарное высказывание, другой - его отрицание.
Теоремы 3,4 позволяют решить вопрос о выполнимости любой формулы алгебры высказываний.
Нужно построить для этой формулы ее ДНФ или ее КНФ. Если построена ДНФ и оказывается, что она удовлетворяет условиям теоремы 4, то формула является невыполнимой. Можно построить КНФ для отрицания исходной формулы. Если окажется, что она удовлетворяет условиям теоремы 3, то исходная формула невыполнима, т. к. ее отрицание тождественно истинно. В остальных случаях формулы являются выполнимыми.
Упражнение 2.2.4
Установить тип формулы S=
.
Определим КНФ для отрицания S:
.
КНФ для 
не удовлетворяет
условию теоремы 3, следовательно, S – выполнима, то есть 
, так как 
.
Обратимся к вопросу о правильности рассуждений. Чтобы убедиться в
том, что рассуждение верно, нужно либо преобразовать импликацию S= P1ÙP2Ù...ÙPn®Q к КНФ и удостовериться в том, что она удовлетворяет
условиям теоремы 3, либо преобразовать к ДНФ и
убедиться в том, что она удовлетворяет условиям теоремы 4.
В упражнении 4.2. 
. Преобразуем S к виду КНФ.
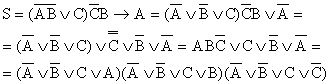
Конъюнктивная нормальная форма удовлетворяет условиям теоремы 3, каждый сомножитель есть тождественно истинное высказывание, а также и их произведение, что и требовалось получить.
Определение 5. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ее ДНФ, обладающая следующими свойствами:
1. Она не содержит двух одинаковых слагаемых.
2. Ни одно слагаемое не содержит одновременно двух одинаковых сомножителей.
3. Ни одно слагаемое не содержит одновременно некоторого высказывания и его отрицания.
4. Каждое слагаемое содержит в качестве сомножителя либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.
Это определение является конструктивным, т.е. позволяет для каждой формулы алгебры высказываний, приведенной к ДНФ, построить ее СДНФ.
Упражнение 2.2.5
.
Задана ДНФ. Приведем ее к СДНФ.
1. Первое и последние слагаемые одинаковы. На основании свойства операции дизъюнкции АÚА=А одно из одинаковых слагаемых можно отбросить.
2. АСС=АС.
3. 
.
Получим 
.
Теперь выполнили условия 1 - 3. Чтобы выполнить условие 4, поступим следующим образом:
;
.
Следовательно, 
.
Теперь условие 4 выполнено, но появились одинаковые слагаемые. Исключив их получим:
.
Определение 6. Совершенной конъюнктивной нормальной формой данной формулы алгебры высказываний (СКНФ) называется такая ее КНФ, которая удовлетворяет следующим свойствам:
1. Она не содержит двух одинаковых сомножителей.
2. Ни один из сомножителей не содержит одновременно двух одинаковых слагаемых.
3. Ни один из сомножителей не содержит одновременно некоторого высказывания и его отрицания.
4. Каждый сомножитель СКНФ содержит в качестве слагаемого либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.
Определение СКНФ также является конструктивным.
Упражнение 2.2.6
Дана КНФ: 
.
Построить СКНФ.
1. АÚВÚВ=АÚВ.
2. (АÚВ)(АÚВ)=АÚВ.
3. 
, следовательно, 
.
4. 
.
Следовательно, 
,
Из определений и теорем 3, 4 следует, что тождественно истинная формула не имеет СКНФ, а тождественно ложная - СДНФ.
Каждая не тождественно истинная и не тождественно ложная формула имеет единственную СКНФ и СДНФ.
Совершенные нормальные формы могут быть применены для установления равносильности двух заданных формул алгебры высказываний. Для этого нужно обе формулы привести к СКНФ или СДНФ и убедить в их совпадении. Например, формулы
и 
равносильны:
.
Полной элементарной конъюнкцией называется конъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 5. Аналогично, полной элементарной суммой называется элементарная дизъюнкция, удовлетворяющая свойствам 2, 3,4 определения 6.
Поэтому совершенные нормальные формы можно определить так:
Определение 7. Совершенной дизъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией различных полных элементарных конъюнкций.
Определение 8. Совершенной конъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией различных полных элементарных дизъюнкций.
Каждая полная элементарная конъюнкция на одном наборе значений
переменных высказываний, ее составляющих, обращается в 1: переменное
высказывание, входящее без знака отрицания, принимает значение 1, а со знаком
отрицания - 0. Этот набор значений элементарных составляющих называется
единицей данной полной элементарной конъюнкции. Так единицей полной
элементарной конъюнкции 
является (1, 0,1).
Аналогично. Каждая полная элементарная дизъюнкция на одном наборе
значений переменных высказываний, ее составляющих, обращается в 0: переменное
высказывание, входящее без знака отрицания, принимает значение 0, а со знаком
отрицания - 1. Этот набор значений элементарных составляющих называется нулем
данной полной элементарной дизъюнкции. Так нулем полной элементарной дизъюнкции
является (1, 1,0).
Эти сведения непосредственно используются в следующем разделе данного учебного пособия.