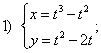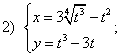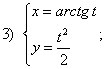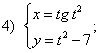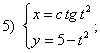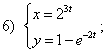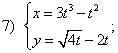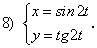Сегодня вы изучите вопросы
-
Производная (или дифференцирование) функции. Задачи, приводящие к понятию производной
-
Односторонние производные
-
Примеры практического применения производной
-
Простейшие правила отыскания производных
-
Производная сложной функции
-
Производная обратной функции
-
Производные основных элементарных функций
-
Параметрическое задание функции и ее производная
-
Производная неявной функции
-
Таблица производных
Изучив тему занятия, вы сможете
-
определить область дифференцируемости функции;
-
найти производные функций, состоящих из основных элементарных функций;
-
найти производные от основных элементарных функций и любой комбинации образования функции от функции (суперпозиции функций), заданных как в явном, так и в неявном виде;
-
найти производные функций, заданных параметрически.
Основные понятия
Предварительно остановимся на понятии касательной к гладкой плоской линии в некоторой ее фиксированной точке. Здесь впервые введено новое понятие «гладкая плоская линия» . Плоская линия называется гладкой, если она является непрерывной, не содержит особых точек, то есть в каждой своей точке имеет единственную касательную. К особым точкам относятся угловые точки
. Плоская линия называется гладкой, если она является непрерывной, не содержит особых точек, то есть в каждой своей точке имеет единственную касательную. К особым точкам относятся угловые точки (рис. 2.1
(рис. 2.1 ), точки заострения
), точки заострения (рис. 2.2
(рис. 2.2 ) и узловые точки
) и узловые точки (рис. 2.3
(рис. 2.3 ).
).
Рассмотрим на плоскости декартовых координат Оху гладкую линию L (рис. 2.4 ).
).
Пусть М — произвольная точка этой линии. Возьмем по обе стороны от М произвольные точки 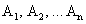 и
и 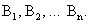
Построим секущие 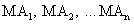 и
и 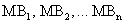 (рис. 2.4).
(рис. 2.4).
При стремлении точек 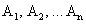 и
и 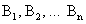 к точке М вдоль линии L секущие вращаются вокруг точки М, и в пределе при
к точке М вдоль линии L секущие вращаются вокруг точки М, и в пределе при 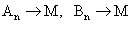 секущие
секущие 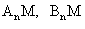 примут предельное положение МТ. Это предельное положение секущих и называется касательной к плоской линии
примут предельное положение МТ. Это предельное положение секущих и называется касательной к плоской линии L в точке М.
L в точке М.
Заметим, что в пределе секущая имеет с плоской гладкой линией единственную точку, называемую точкой касания , а в точках линий, содержащих угловые точки, узловые точки и точки заострения, предельные положения секущих не совпадают.
, а в точках линий, содержащих угловые точки, узловые точки и точки заострения, предельные положения секущих не совпадают.
Задача Лейбница о касательной к плоской гладкой линии. На плоскости декартовых координат Оху дана плоская гладкая линия уравнением у = f(x) (рис. 2.5 ).
).
Пусть 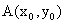 произвольная точка графика этой функции. Требуется найти уравнение касательной к графику этой функции в точке
произвольная точка графика этой функции. Требуется найти уравнение касательной к графику этой функции в точке 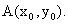 Пусть
Пусть 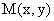 — произвольная точка графика функции. Построим касательную АТ и секущую АМ. Углы, образованные касательной и секущей с осью Ох, обозначим соответственно через φ и
— произвольная точка графика функции. Построим касательную АТ и секущую АМ. Углы, образованные касательной и секущей с осью Ох, обозначим соответственно через φ и 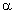 .
.
Предельным положением секущей АМ является касательная АТ. Введем обозначения: 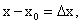
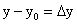 . При движении точки М по направлению к точке А вдоль линии у = f(x) приращение аргумента
. При движении точки М по направлению к точке А вдоль линии у = f(x) приращение аргумента 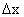 стремится к нулю; угол
стремится к нулю; угол 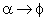 , следовательно,
, следовательно, 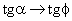 :
: 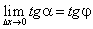 . Так как
. Так как 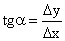 , то окончательно находим, что:
, то окончательно находим, что:
Известно, что уравнение касательной как прямой, проходящей через точку 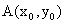 и образующей с осью Ох угол φ, имеет вид:
и образующей с осью Ох угол φ, имеет вид:
С учетом равенства (32) окончательно находим уравнение искомой касательной:
Таким образом, для отыскания уравнения касательной к плоской линии нам необходимо вычислить предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
Задача Ньютона о мгновенной скорости. Вначале определим понятие мгновенной скорости. Пусть тело М движется вдоль оси Оs c произвольной скоростью (рис. 2.6 ). Пусть в момент времени t тело находилось в точке
). Пусть в момент времени t тело находилось в точке 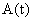 , а в момент времени
, а в момент времени 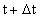 тело находилось в точке
тело находилось в точке 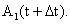 Очевидно, пройденный телом М путь является функцией времени.
Очевидно, пройденный телом М путь является функцией времени.
Пусть эта зависимость задается функцией 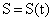 .
.
Обозначим пройденные телом М пути соответственно следующим образом:
За величину скорости тела М в момент времени t (или в точке А) принимается предел средней скорости на участке
М в момент времени t (или в точке А) принимается предел средней скорости на участке 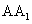 при
при 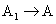 (или при
(или при 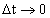 ).
).
Скорость в фиксированный момент времени t называется мгновенной скоростью в момент времени t и символически обозначается так:
и символически обозначается так: 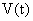 .
.
Таким образом, по определению:
И вновь задача об отыскании мгновенной скорости свелась к вычислению предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
Задача о производительности труда. Пусть функция 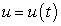 выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент t0.
выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент t0.
Очевидно, за период времени от t0 до 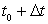 количество произведенной продукции изменится от значения
количество произведенной продукции изменится от значения 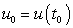 до значения
до значения 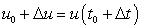 ; тогда средняя производительность труда за этот период времени
; тогда средняя производительность труда за этот период времени 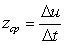 . Очевидно, что производительность труда в момент t0 можно определить как предельное значение средней производительности за период времени от t0 до
. Очевидно, что производительность труда в момент t0 можно определить как предельное значение средней производительности за период времени от t0 до 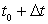 при
при 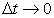 , т.е.:
, т.е.: 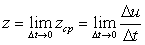 .
.
Рассматривая три различные по характеру задачи, мы пришли к пределу одного вида. Этот предел играет чрезвычайно важную роль в математическом анализе, являясь основным понятием дифференциального исчисления.
Пусть на отрезке [a, b] задана функция у = у(x). Пусть х = х0 — произвольная внутренняя точка этого отрезка, а y0 — соответствующее значение функции в точке х = х0: 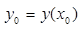 . Придадим
. Придадим 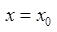 приращение ∆x такое, чтобы не выйти за пределы заданного отрезка. Обозначим через y(x0 + ∆x) новое значение заданной функции, а через ∆y0 — приращение функции у = у(х) в т. х = х0:
приращение ∆x такое, чтобы не выйти за пределы заданного отрезка. Обозначим через y(x0 + ∆x) новое значение заданной функции, а через ∆y0 — приращение функции у = у(х) в т. х = х0:
Производной функции у = f(x) в точке x = x0 называется конечный (или бесконечный) предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
у = f(x) в точке x = x0 называется конечный (или бесконечный) предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
Символически производная от функции у = f(x) обозначается так:
Таким образом, по определению:
Производная функции у = f(x) в произвольной внутренней точке 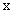 области определения функции обозначается так:
области определения функции обозначается так:
Если функция у = f(x) имеет производную в произвольной точке х некоторого множества значений х области определения функции у = f(x), то функция у = f(x) называется дифференцируемой на этом множестве .
.
Равенство (37) является частным значением производной в точке 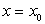 .
.
На основании введенного определения и рассмотренных нами задач, приводящих к понятию производной, заключаем, что уравнение касательной к графику функции в точке с абсциссой 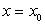 имеет вид:
имеет вид:
а мгновенная скорость равна:
т.е. скорость материального тела в момент времени t равна производной от пути по времени, найденной для этого момента времени.
К примерам отыскания касательных к плоским линиям и мгновенной скорости мы обратимся после того, как научимся находить производные основных элементарных функций, сложных функций, обратных функций, изучим основные теоремы дифференцирования.
После определения понятия производной можно заключить, что:
где 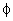 — угол наклона касательной к графику функции у = f(x) в точке с абсциссой х. В этом и заключается геометрический смысл производной
— угол наклона касательной к графику функции у = f(x) в точке с абсциссой х. В этом и заключается геометрический смысл производной .
.
А мгновенная скорость равна:
т.е. производной от пути по времени ; в этом заключается физический смысл производной
; в этом заключается физический смысл производной .
.
Из определения производной следует, что производная есть предел функции . Из теории пределов следует, что предел (38) существует, если существуют односторонние пределы в точке
. Из теории пределов следует, что предел (38) существует, если существуют односторонние пределы в точке 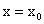 , которые должны быть равны между собой. Что касается пределов для границ отрезка
, которые должны быть равны между собой. Что касается пределов для границ отрезка 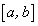 , то для этих точек нами были определены только односторонние пределы: для точки
, то для этих точек нами были определены только односторонние пределы: для точки 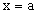 — предел справа, для точки
— предел справа, для точки 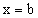 — предел слева. По аналогии для производной функции у = f(x) на концах отрезка
— предел слева. По аналогии для производной функции у = f(x) на концах отрезка 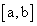 также вводятся понятия односторонних пределов
также вводятся понятия односторонних пределов
называемых односторонними производными .
.
Таким образом, из определения производной функции у = f(x) следует, что для существования производной этой функции в точке 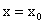 необходимо и достаточно, чтобы существовали (конечные или бесконечные) в этой точке односторонние производные
необходимо и достаточно, чтобы существовали (конечные или бесконечные) в этой точке односторонние производные 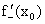 и
и 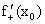 , равные между собой:
, равные между собой:
Геометрически равенство бесконечности производной в некоторой точке 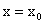 означает, что касательная к графику функции в точке, абсцисса которой равна
означает, что касательная к графику функции в точке, абсцисса которой равна 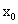 , параллельна оси Оу (или перпендикулярна оси Ох).
, параллельна оси Оу (или перпендикулярна оси Ох).
На рис. 2.5 графиком функции у = f(x) является гладкая линия, односторонние производные (касательные слева и справа) в любой ее точке совпадают. На рисунках 2.1, 2.2, 2.3 функции, представленные своими графиками, имеют особые точки.
Как следует из рисунков, в особых точках эти касательные не совпадают, т.е. односторонние производные существуют, но не равны между собой.
При построении графиков функций существенную роль играет геометрическое представление равенства бесконечности односторонних пределов. На рис. 2.7 представлены возможные варианты равенства бесконечности односторонних производных.
представлены возможные варианты равенства бесконечности односторонних производных.
Дадим некоторые пояснения к рисунку 2.7. На рис. а), б), в) имеется единственная касательная к графику функции в т. А. Если за х обозначить абсциссу точки А, то для случая а) 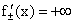 , для варианта б)
, для варианта б) 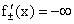 , для случая в) и г) односторонние пределы бесконечны, но отличны по знаку, для случая д)
, для случая в) и г) односторонние пределы бесконечны, но отличны по знаку, для случая д) 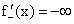 , для случая е)
, для случая е) 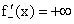 , для случая ж)
, для случая ж) 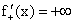 .
.
Естественно, после введения понятия производной напрашивается вопрос: при каких условиях существует производная заданной функции?
Следующая теорема частично отвечает на поставленный вопрос.
Теорема 14 о непрерывности дифференцируемой функции — необходимое условие дифференцируемости функции.
Если функция у = f(x) дифференцируема в точке 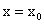 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. По условию теоремы дано, что существует конечный предел:
По теореме 2 о связи предела с б.м.в. имеем:
Из равенства (45) следует, что:
Отсюда находим, что:
Этим доказана непрерывность функции в точке 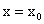 .
.
Таким образом, из дифференцируемости функции в точке непременно следует ее непрерывность в этой точке. Это условие является необходимым. Однако обратное утверждение не всегда имеет место, т.е. из непрерывности функции еще не следует ее дифференцируемость. Наглядным примером тому являются функции, имеющие особые точки (рис. 2.1, 2.2, 2.3): на этих рисунках функции представлены неразрывными линиями (т.е. они представляют графики непрерывных функций), в особых же точках заданные функции не имеют производных (односторонние производные не равны между собой).
Классическим примером такой функции является функция 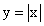 (рис. 2.8
(рис. 2.8 ), которая непрерывна в точке х = 0, но производная этой функции в т. х = 0 не существует, так как
), которая непрерывна в точке х = 0, но производная этой функции в т. х = 0 не существует, так как 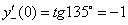 , а
, а 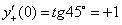 .
.
Сформулируем четырехступенчатое правило отыскания производной.
Из определения производной следует, что для отыскания производной необходимо найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е. 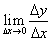 .
.
Отсюда следующее правило:
-
Придаем независимой переменной х приращение
 ; находим новое значение функции
; находим новое значение функции 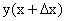 : для получения нового значения функции у = f(x) надо подставить в правую часть этого равенства вместо х выражение
: для получения нового значения функции у = f(x) надо подставить в правую часть этого равенства вместо х выражение 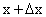 .
. -
Находим приращение функции
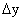 путем вычитания из нового значения
путем вычитания из нового значения 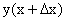 старого значения
старого значения 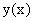 :
: -
Составляем отношение приращения функции
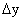 к приращению аргумента:
к приращению аргумента: 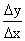 .
.
В качестве примера найдем производную от постоянной величины, производную независимой переменной по самой переменной, производную от квадратичной функции, производную от логарифмической функции, производную от тригонометрической функции.
В силу существования предела по определению производной имеем: 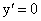 , или, подставляя вместо
, или, подставляя вместо 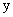 ее выражение
ее выражение 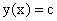 , окончательно находим:
, окончательно находим:
т.е. производная постоянной величины равна нулю.
В силу существования предела по определению производной имеем: 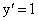 , или, подставляя вместо
, или, подставляя вместо 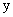 ее выражение
ее выражение 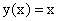 , окончательно находим:
, окончательно находим:
т.е. производная переменной по самой переменной равна 1.
-
Новое значение функции равно:
-
Приращение функции равно:
-
Находим предел:
В силу существования предела по определению производной имеем: 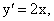 или, подставляя вместо функции
или, подставляя вместо функции 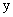 ее выражение
ее выражение 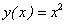 , окончательно находим:
, окончательно находим:
-
Новое значение функции равно:
-
Приращение функции равно:
-
Находим предел:
В силу существования предела по определению производной имеем: 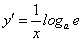 , или, подставляя вместо функции у ее выражение
, или, подставляя вместо функции у ее выражение 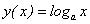 , окончательно находим:
, окончательно находим:
или, с учетом равенства 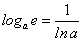 , окончательно получим:
, окончательно получим:
Отсюда, в частности, при 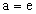 будем иметь:
будем иметь:
-
Приращение функции равно:
-
Находим предел:
В силу существования предела по определению производной имеем: 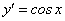 , или, подставляя вместо у ее выражение
, или, подставляя вместо у ее выражение 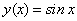 , окончательно находим:
, окончательно находим:
Пример 6. Написать уравнение касательной и нормали к кривой:
f(x) = x2 + 4x + 5 в точке М0(-1; 2).
Уравнение касательной к плоской кривой 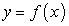 определяется по формуле:
определяется по формуле:
а нормали — по следующей формуле:
По условию задачи задана точка М0(-1; 2), лежащая на заданной кривой.
Следовательно, х0 = -1; у0 = 2.
Для нахождения искомых линий достаточно найти производную заданной функции при х = -1.
Находим:
Следовательно, искомыми касательная будут:
Найти скорость движения в момент 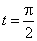 .
.
Пусть функции 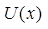 и
и 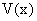 — дифференцируемые функции на множестве
— дифференцируемые функции на множестве 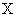 .
.
Найдем, чему равны производные от функций, полученных из 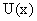 и
и 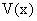 путем арифметических действий:
путем арифметических действий:
Теорема 15. Производная алгебраической суммы дифференцируемых функций равна алгебраической сумме производных этих функций, т.е.:
По условиям теоремы дано, что существуют конечные пределы:
Доказательство. Для простоты проведем доказательство для суммы. Введем обозначение: Y(x) = U(x) + V(x). Найдем производную функции 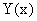 по четырехступенчатому правилу.
по четырехступенчатому правилу.
-
Придадим х приращение
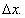 Найдем новое (приращенное) значение функции:
Найдем новое (приращенное) значение функции: -
Найдем отношение:
-
Находим предел:
Из равенства (55) следует, что предел слева в равенстве (56) существует, следовательно, 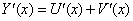 , или, с учетом введенного обозначения, окончательно получим:
, или, с учетом введенного обозначения, окончательно получим:
Предоставляем читателю самостоятельно доказать справедливость равенства:
Равенство (54) справедливо и при любом конечном числе слагаемых.
Теорема 16. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую и производной второй функции на первую, т.е.:
По условиям теоремы дано, что существуют конечные пределы:
Доказательство. Введем обозначение: Y(x) = U(x) ∙ V(x). Найдем производную функции 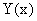 по четырехступенчатому правилу.
по четырехступенчатому правилу.
Из равенства (59) следует, что существует предел справа.
Следовательно, существует и предел слева:
или, с учетом введенного обозначения, окончательно получим:
Следствие 1. В частности, если одна из функции есть постоянная величина, например 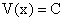 , то из равенства (59) следует:
, то из равенства (59) следует:
т.е. постоянный множитель можно выносить за знак произведения.
Следствие 2. Производная произведения любого конечного числа дифференцируемых функций равна сумме произведений производной первой функции на все остальные плюс производная второй функции на все остальные и т.д. плюс производная последней функции на все остальные:
Доказательство предоставляем читателю.
Теорема 17. Производная частного двух дифференцируемых функций равна дроби, числитель которой равен разности произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель равен квадрату знаменателя данной дроби, если знаменатель отличен от нуля, т.е.:
По условиям теоремы дано, что существуют конечные пределы:
Требуется доказать справедливость равенства (62).
Доказательство можно провести аналогично приведенному выше доказательству (доказательство предоставляется читателю).
Следствие 1. Если V(х) = с — константа, то формула (62) переписывается так:
Следствие 2. Если V(х) = с — константа, то формула (62) переписывается так:
Пусть у = f(u), где u ϵ U, а u = u(х), где х ϵ Х, u ϵ U. Тогда переменная у является сложной функцией независимой переменной х на множестве х ϵ Х, u — промежуточная переменная.
Найдем формулу для производной сложной функции 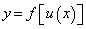 по независимой переменной х при следующих предположениях: функция у = f(u) дифференцируема по u на множестве U, функция u = u(х) является дифференцируемой на множестве Х.
по независимой переменной х при следующих предположениях: функция у = f(u) дифференцируема по u на множестве U, функция u = u(х) является дифференцируемой на множестве Х.
Докажем, что справедливо равенство:
т.е. производная сложной функции по независимой переменной равна произведению производной этой функции по промежуточной переменной на производную промежуточной переменной по независимой переменной.
По условию существуют конечные пределы:
Из существования конечного предела 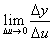 следует, что:
следует, что:
Отсюда находим:
В равенстве (67) перейдем к пределу при ∆х → 0.
По условию u = u(х) непрерывная функция, т.к. она дифференцируема. Следовательно, при ∆х → 0 и ∆u → 0.
Отсюда равенство (68) перепишется так:
В силу существования предела справа предел слева тоже существует и по определению называется 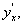 т. о. имеем:
т. о. имеем: 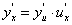 , ч.т.д.
, ч.т.д.
Если функция у = f(х) на множестве Х дифференцируема, то в точках, где ее производная отлична от нуля, обратная функция х = φ(у) дифференцируема и равна обратной величине производной прямой функции у = f(х), т.е.
Доказательство проведем для монотонной функции у = f(х). По условию прямая функция у = f(х) дифференцируема на множестве Х, следовательно, она непрерывна на этом множестве. Так как функция у = f(х) на множестве Х однозначна и монотонна, то для произвольной точки х ϵ Х справедливо следующее рассуждение: если изменить х на ∆х ≠ 0, то соответствующее значение функции у(х) изменится на ∆у ≠ 0.
Пусть Y — множество значений функции у = f(х).
По теореме о существовании обратной функции на множестве Y будет определена непрерывная и монотонная функция х = φ(у).
Для отыскания ее производной по переменной у найдем предел отношения:
Т.к. функция у = f(х) непрерывна, то при ∆х → 0 и ∆у → 0, и наоборот. Следовательно, в (70) предел при ∆у → 0 можно заменить на ∆х → 0. Так как по условию пределы числителя и знаменателя существуют и предел знаменателя отличен от 0, то 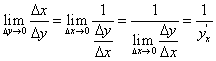 , или
, или 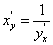 , ч.т.д.
, ч.т.д.
На предыдущем занятии по четырехступенчатому правилу нами была найдена производная логарифмической функции:
в частности, при а = е мы получили:
Рассмотрим сложную функцию 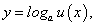 удовлетворяющую всем условиям существования производной сложной функции.
удовлетворяющую всем условиям существования производной сложной функции.
Как будет выглядеть производная функции 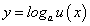 ? Последнюю функцию нужно рассматривать как сложную функцию
? Последнюю функцию нужно рассматривать как сложную функцию 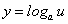 , где
, где 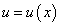 .
.
По теореме о производной сложной функции имеем:
Таким образом, нами найдена производная сложной функции 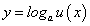 :
:
Отсюда, в частности, при а = е получим:
Производная показательной функции
Рассмотрим показательную функцию
Найдем производную функции (75), воспользовавшись производной логарифмической функции.
Прологарифмируем обе части равенства 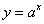 по основанию
по основанию 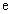 :
:
Возьмем от обеих частей равенства (76) производную по х, рассматривая левую часть этого равенства как сложную функцию от х:
Подставляя вместо функции 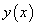 ее выражение
ее выражение 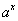 , получим:
, получим:
Рассмотрим сложную функцию 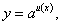 которая удовлетворяет условиям существования сложной функции.
которая удовлетворяет условиям существования сложной функции.
По теореме о производной сложной функции имеем:
Окончательно находим:
В частности, при а = е получим:
Производная степенной функции
Найдем производную степенной функции 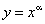 , где α — произвольное действительное число.
, где α — произвольное действительное число.
Прологарифмируем обе части равенства 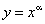 по основанию
по основанию 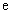 :
:
Возьмем от обеих частей равенства (81) производную по х, воспользовавшись формулами (72) и (73):
Подставим в последнем равенстве вместо у(х) степенную функцию 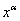 :
:
Окончательно получим:
В случае задания сложной степенной функции 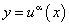 по аналогии с вышеизложенным получим:
по аналогии с вышеизложенным получим:
Отсюда, в частности, при 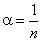 получим:
получим:
или окончательно:
Отсюда при n = 2 получим:
Производная показательно-степенной функции
Рассмотрим функцию 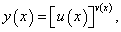 заданную на множестве Х, где выполняются условия существования производной сложной функции: функции
заданную на множестве Х, где выполняются условия существования производной сложной функции: функции 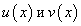 дифференцируемы, функция у дифференцируема по u и v.
дифференцируемы, функция у дифференцируема по u и v.
Для отыскания искомой производной возьмем от обеих частей равенства 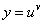 натуральный логарифм:
натуральный логарифм:
Возьмем от обеих частей равенства (86) производную по х, воспользовавшись формулой (73) и производной произведения:
Подставляя в равенстве (87) вместо 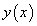 показательно-степенную функцию
показательно-степенную функцию 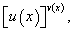 получим:
получим:
или окончательно:
Из формулы (88) следует, что производная показательно-степенной функции равна сумме производных от функции 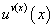 , которая вначале рассматривается как показательная функция, а затем как степенная.
, которая вначале рассматривается как показательная функция, а затем как степенная.
Производные тригонометрических функций
На предыдущем занятии (занятие 5) нами была найдена производная 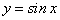 по четырехступенчатому правилу, и было установлено, что:
по четырехступенчатому правилу, и было установлено, что:
Если дана сложная функция 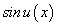 , то по формуле производной сложной функции находим:
, то по формуле производной сложной функции находим:
Найдем у’, воспользовавшись формулами приведения и формулой (89).
Имеем:
Отсюда окончательно:
Таким образом,
По аналогии, в случае задания сложной функции 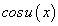 будем иметь:
будем иметь:
Для отыскания производной воспользуемся формулой для производной дроби:
Таким образом,
В случае задания сложной функции по аналогии получим:
Для отыскания производной 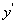 воспользуемся формулой приведения и формулой (93) для производной
воспользуемся формулой приведения и формулой (93) для производной 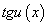 :
:
Таким образом, имеем:
В случае задания сложной функции будем иметь:
Производные обратных тригонометрических функций
-
Так как функция
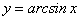 на заданном отрезке монотонна и непрерывна, то по теореме о существовании обратной функции функция
на заданном отрезке монотонна и непрерывна, то по теореме о существовании обратной функции функция 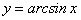 имеет обратную функцию
имеет обратную функцию 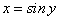 . Так как производная обратной функции отлична от нуля
. Так как производная обратной функции отлична от нуля 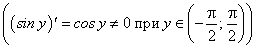 , то по теореме о производной обратной функции имеем:
, то по теореме о производной обратной функции имеем:Здесь мы воспользовались основным тригонометрическим тождеством
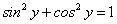 .
.Отсюда находим, что
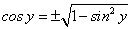 . Перед радикалом в равенстве (96) взят знак «плюс», т.к. cos y на интервале
. Перед радикалом в равенстве (96) взят знак «плюс», т.к. cos y на интервале 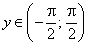 является величиной положительной. Подставляя вместо у(x) обратную тригонометрическую функцию arcsinx, получим:
является величиной положительной. Подставляя вместо у(x) обратную тригонометрическую функцию arcsinx, получим: -
На интервале (-1; 1) функция
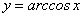 монотонна и непрерывна. По теореме о существовании обратной функции функция
монотонна и непрерывна. По теореме о существовании обратной функции функция 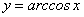 имеет обратную функцию
имеет обратную функцию 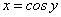 , которая на интервале
, которая на интервале 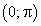 по переменной у имеет производную, отличную от нуля. Следовательно, по теореме о производной обратной функции имеем:
по переменной у имеет производную, отличную от нуля. Следовательно, по теореме о производной обратной функции имеем:По тем же соображениям перед радикалом взят знак «плюс», т.к. функция ]
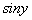 на интервале
на интервале 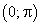 положительна.
положительна.В случае задания сложной функции по аналогии получим:
-
Функция
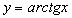 на заданном интервале монотонна и непрерывна, следовательно, на соответствующем интервале
на заданном интервале монотонна и непрерывна, следовательно, на соответствующем интервале 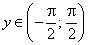 определена однозначная обратная функция
определена однозначная обратная функция 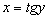 . Заметим, что производная функции
. Заметим, что производная функции 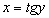 отлична от нуля. Тогда по теореме о производной обратной функции:
отлична от нуля. Тогда по теореме о производной обратной функции: -
Функция
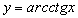 на интервале
на интервале 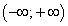 монотонна и непрерывна. По теореме о существовании обратной функции заданная функция имеет обратную
монотонна и непрерывна. По теореме о существовании обратной функции заданная функция имеет обратную 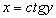 , которая на интервале
, которая на интервале 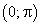 также монотонна и непрерывна. Заметим, что
также монотонна и непрерывна. Заметим, что 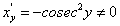 при
при 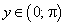 . Тогда, по теореме о производной обратной функции имеем:
. Тогда, по теореме о производной обратной функции имеем:
В качестве примера рассмотрим окружность в прямоугольной системе координат Оху (рис. 2.9 ).
).
Пусть М (х; у) — произвольная точка окружности; |ОМ|= R — радиус окружности.
По определению тригонометрических функций 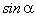 и
и 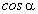 имеем:
имеем:
Равенствами (105) зависимость функции у от х задается через угол α, который является параметром.
Легко заметить, что из равенства (105) следует:
что является известным каноническим уравнением окружности.
В общем случае функция у от переменной х называется заданной параметрически, если эта зависимость задается системой равенств (106):
Найдем производную от функции, заданной параметрически равенствами (106). Пусть 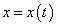 удовлетворяет всем условия дифференцируемости и существования обратной функции
удовлетворяет всем условия дифференцируемости и существования обратной функции 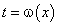 , где
, где 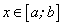 : функция
: функция 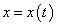 монотонна и непрерывна на отрезке
монотонна и непрерывна на отрезке 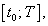 существует конечный предел
существует конечный предел 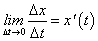 , отличный от нуля.
, отличный от нуля.
Переменную у можно рассматривать как сложную функцию переменной х на отрезке 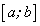 :
:
По теореме о производной сложной функции имеем:
Так как производная обратной функции 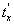 равна обратной величине производной прямой функции, т.е.
равна обратной величине производной прямой функции, т.е. 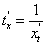 , то равенство (107) можно переписать так:
, то равенство (107) можно переписать так:
Пример. Функция 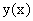 переменной х задана параметрически:
переменной х задана параметрически:
Найдем производную второго порядка от функции, заданной параметрически.
Функция 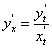 является сложной функцией переменной х. По теореме о производной сложной функции имеем:
является сложной функцией переменной х. По теореме о производной сложной функции имеем:
Пусть уравнение:
на множестве Х задает неявную функцию 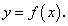 Общая формула для отыскания производной неявной функции задается в разделе функций многих переменных. Однако если в уравнении (110) рассматривать переменную y как функцию переменной х, то, взяв производную по х от обеих частей равенства (110) и разрешив относительно
Общая формула для отыскания производной неявной функции задается в разделе функций многих переменных. Однако если в уравнении (110) рассматривать переменную y как функцию переменной х, то, взяв производную по х от обеих частей равенства (110) и разрешив относительно 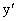 , можно найти искомую производную как функцию переменных х и у.
, можно найти искомую производную как функцию переменных х и у.
Действительно, уравнение
на множестве 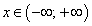 определяет неявную функцию
определяет неявную функцию 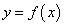 .
.
Возьмем от обеих частей уравнения (111) производную по х:
Решив уравнение (112) относительно 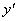 , находим:
, находим:
На основе найденных производных основных элементарных функций составим таблицу производных. В нижеприведенную таблицу включены также основные правила дифференцирования.
1. 14. 2. 15. 3. 16. 4. 17. 5. 18. 6. 19. 7. 8. 9. 22. 10. 23. 11. 24. 12. 25. 13.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
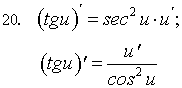
![]()
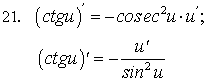
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим примеры на отыскание производных заданных функций по таблице производных и основным правилам взятия производных дифференцируемых функций.
Пример 1. Найти производную функции:
у = 2х4 + 4х2 + 3х2 + 5х — 2.
На основании правил дифференцирования и формулы производной степенной функции имеем:
y' = (2х4 + 4х3 + 3х2 + 5х — 2)' = (2x4)' + (4x3)' + (3x2)' + (5x)' — (2)' = 2(x4)' + 4(x3)' + 3(x2)' +
+ 5(x)' — 0 = 2 ∙ 4x3 + 4 ∙ 3x2 + 3 ∙ 2x + 5 = 8x3 + 12x2 + 6x + 5.
Пример 2. Найти производную функции:
Имеем:
Пример 3. Дана функция f(x) = x3 — 4x — 1.
-
Сначала находим производную заданной функции:
-
Подставляем в выражение первой производной вместо х последовательно числа -2; -1; 0; 1; 3:
Пример 4. Найти производную функции:
у = х2 sinx — x ∙ cosx.
Производную находим по правилу производной от алгебраической суммы и по формуле производной от произведения дифференцируемых функций.
Имеем:
Искомую производную найдем по формуле производной от дроби:
Пример 6. Найти производную сложных функций:
1. Если предположить, что 4х = u, то функцию у = cos 4х можно рассматривать как сложную функцию:
y = cos u, u = 4x.
По правилу нахождения производной сложной функции имеем:
При нахождении производных сложных функций в дальнейшем мы будем пользоваться соответствующими формулами дифференцирования сложных функций.
Пример 7. Найти производную от функции, заданной неявно:
ху + sinу = 0.
Чтобы найти производную 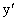 от неявной функции, нужно продифференцировать по х обе части заданного равенства, рассматривая переменную у как функцию от х, найти
от неявной функции, нужно продифференцировать по х обе части заданного равенства, рассматривая переменную у как функцию от х, найти 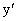 из полученного равенства.
из полученного равенства.
Имеем:
Контрольные вопросы
-
Дайте определение производной функции в точке.
-
Найдите по четырехступенчатому правилу производную функции у(х) = х2.
-
На основании основных правил взятия производных найдите производную функции у(х) = 5х2 — 3х + 4.
-
Непрерывность функции является необходимым или достаточным условием?
-
Для существования производной в точке каковы ее достаточные условия?
-
Перечислите наименования точек разрыва производной непрерывной функции.
-
Каков геометрический смысл производной?
-
Каков механический смысл первой производной?
-
Приведите пример применения понятия производной функции в экономике.
-
Дайте определение касательной к графику функции
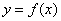 в точке
в точке 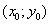 и напишите уравнение касательной.
и напишите уравнение касательной. -
Какая функция называется неявно заданной?
-
Какая функция называется параметрически заданной?
-
Приведите формулы для нахождения производных арксинуса, арккосинуса, арктангенса и арккотангенса.
-
Приведите формулу для нахождения производной первого порядка параметрически заданной функции.
-
Сформулируйте правило нахождения производной неявно заданной функции.
Задания для самостоятельной работы
-
Воспользовавшись четырехступенчатым правилом дифференцирования, найдите производную функции
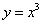 .
. -
Найдите производные следующих функций, пользуясь формулами и правилами дифференцирования:
-
Напишите уравнение касательной и нормали к параболе
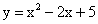 в точке, абсцисса которой равна
в точке, абсцисса которой равна 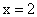 .
. -
Найдите мгновенную скорость движения тела в момент t = 2 ч., если известно, что закон, выражающий зависимость пройденного пути от времени, имеет вид
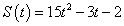 .
. -
Найдите производные следующих функций:
-
Найдите производные неявных функций:
-
Найдите уравнения касательной и нормали к плоской линии y = e3x в точке M0 (0; 1).
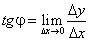 . (32)
. (32)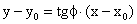 . (33)
. (33)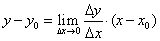 . (34)
. (34)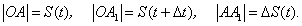
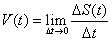 . (35)
. (35)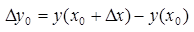
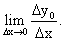 (36)
(36)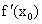 или
или 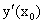 — по Лагранжу;
— по Лагранжу;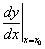 — по Лейбницу;
— по Лейбницу;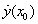 — по Ньютону.
— по Ньютону.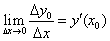 . (37)
. (37)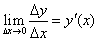 . (38)
. (38)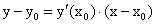 , (39)
, (39)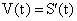 , (40)
, (40)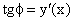 , (41)
, (41)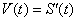 , (42)
, (42)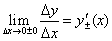 , (43)
, (43)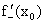 =
= 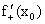 .
.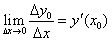 . (44)
. (44)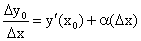 , (45)
, (45)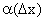 — б.м.в. при
— б.м.в. при 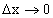 :
: 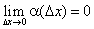 .
.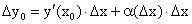 . (46)
. (46)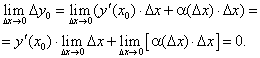
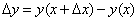 .
.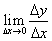 .
.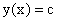 , где
, где 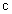 —
— 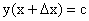 .
.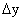 =
= 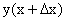 —
— 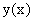 =
= 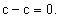
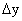 к приращению аргумента равно:
к приращению аргумента равно: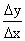 =
= 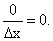
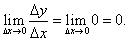
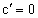 , (47)
, (47)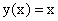
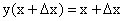 .
.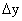 =
= 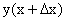 —
— 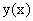 =
= 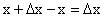 .
.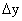 к приращению аргумента равно:
к приращению аргумента равно: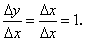
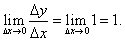
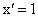 , (48)
, (48)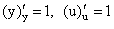 и т.д.
и т.д.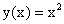 .
.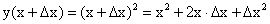 .
.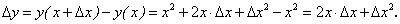
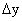 к приращению аргумента равно:
к приращению аргумента равно: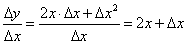 .
.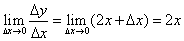 .
.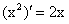 . (49)
. (49)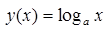 , где
, где 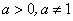 .
.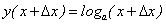 .
.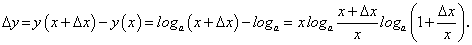
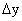 к приращению аргумента равно:
к приращению аргумента равно: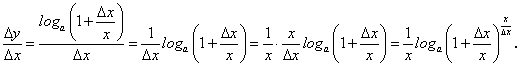
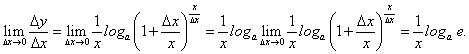
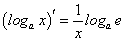 , (50)
, (50)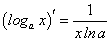 . (51)
. (51)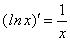 . (52)
. (52)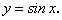
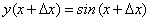 .
.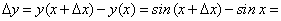
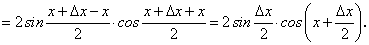
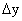 к приращению аргумента равно:
к приращению аргумента равно: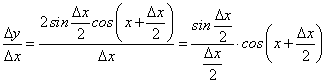 .
.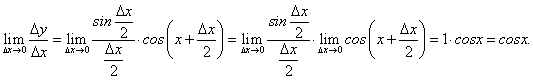
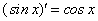 . (53)
. (53)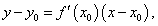
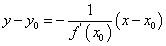 .
.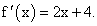
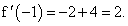
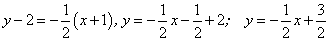 — нормаль.
— нормаль.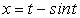 .
.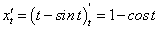 .
.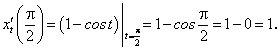
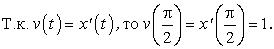
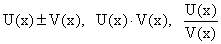 (при
(при 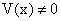 ),
),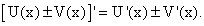 (54)
(54)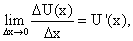
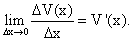 (55)
(55)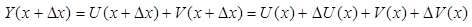 .
.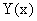 :
: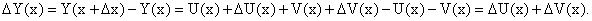
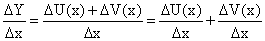 .
.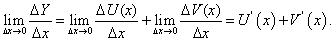 (56)
(56)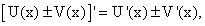 ч.т.д.
ч.т.д.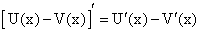 . (57)
. (57)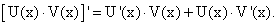 (58)
(58)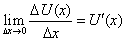 ,
, 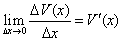 .
. приращение
приращение 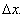 Найдем новое (приращенное) значение функции:
Найдем новое (приращенное) значение функции: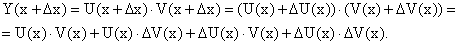
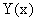 :
: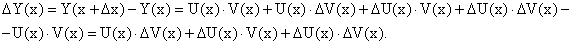
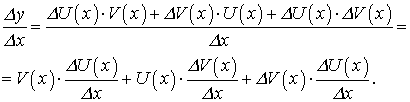
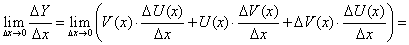
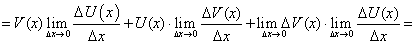
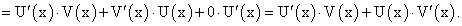
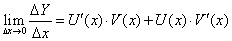 . (59)
. (59)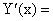
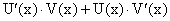 ,
,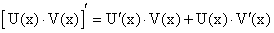 , ч.т.д.
, ч.т.д.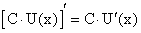 , (60)
, (60)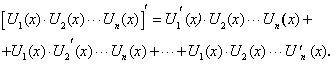 (61)
(61)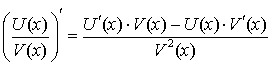 . (62)
. (62)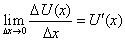 ,
, 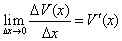 и
и 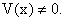
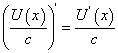 . (63)
. (63)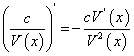 . (64)
. (64)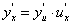 , (65)
, (65)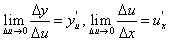 (66)
(66)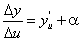 , где
, где 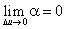 ; или
; или 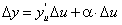 .
.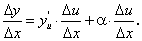 (67)
(67)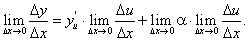 (68)
(68)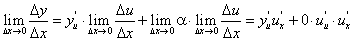 .
.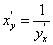 (69)
(69)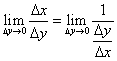 . (70)
. (70)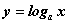
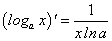 , (71)
, (71)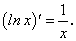 (72)
(72)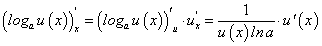 .
.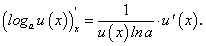 (73)
(73)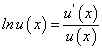 . (74)
. (74)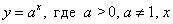
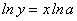 . (76)
. (76)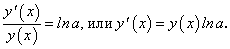
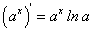 . (77)
. (77)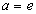 имеем:
имеем: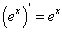 . (78)
. (78)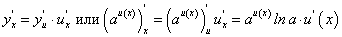 .
.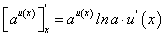 . (79)
. (79)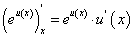 . (80)
. (80)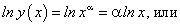
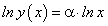 . (81)
. (81)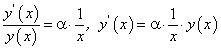 .
.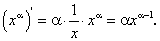
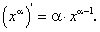 (82)
(82)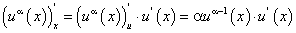 , или
, или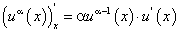 . (83)
. (83)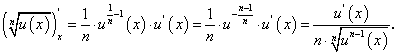
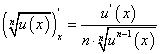 . (84)
. (84)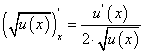 . (85)
. (85)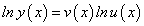 . (86)
. (86)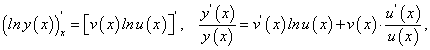
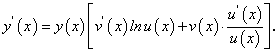 (87)
(87)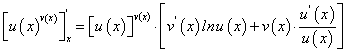 ,
,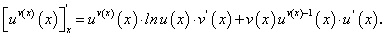 (88)
(88)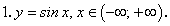
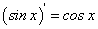 . (89)
. (89)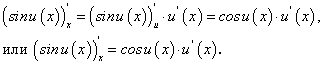 (90)
(90)
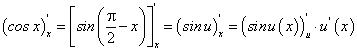 ,
,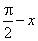 :
: 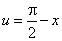 .
.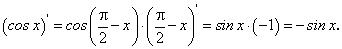
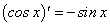 . (91)
. (91)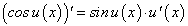 .
.
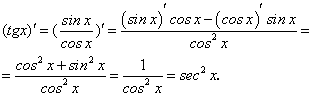
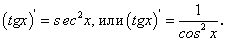 (92)
(92)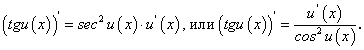 (93)
(93)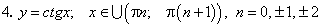 .
.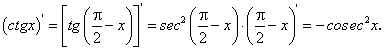
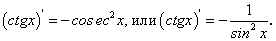 (94)
(94)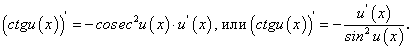 (95)
(95)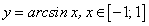 .
.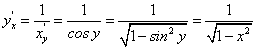 . (96)
. (96)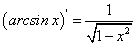 . (97)
. (97)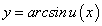 получим:
получим: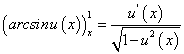 . (98)
. (98)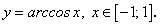
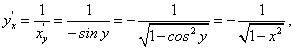 или
или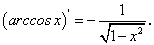 (99)
(99)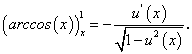 (100)
(100)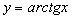 ,
, 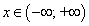 .
.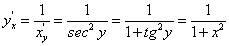 , или
, или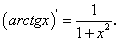 (101)
(101) получим:
получим: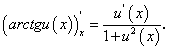 (102)
(102)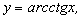
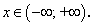
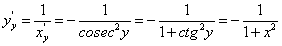 , или
, или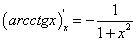 . (103)
. (103)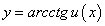 по аналогии будем иметь:
по аналогии будем иметь: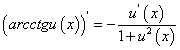 . (104)
. (104)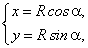 (105)
(105)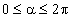 .
.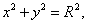
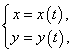 (106)
(106)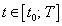 .
.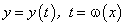 .
.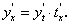 (107)
(107)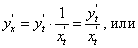
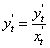 . (108)
. (108)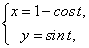
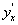 . По формуле (108) имеем:
. По формуле (108) имеем: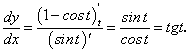
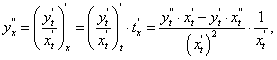
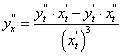 . (109)
. (109)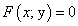 (110)
(110)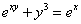 (111)
(111)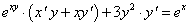 (112)
(112)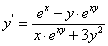 .
.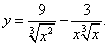
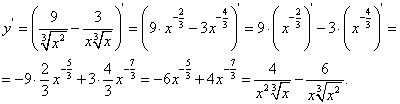
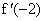 ,
, 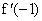 ,
, 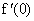 ,
, 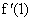 ,
, 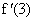 .
.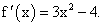
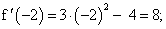
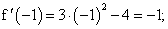
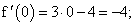
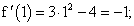
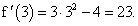
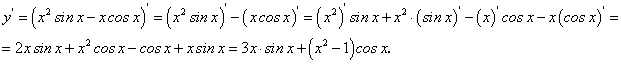
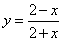 .
.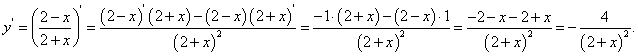
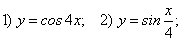
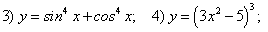
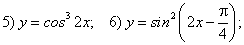
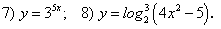
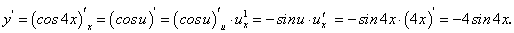
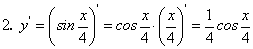 .
.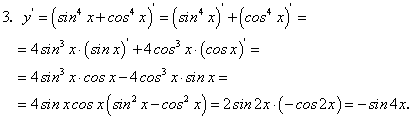
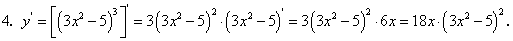
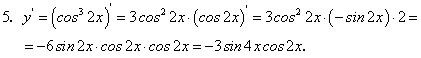
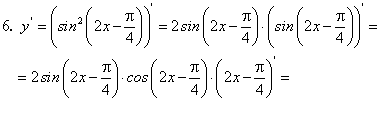
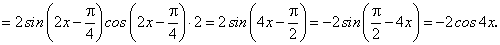
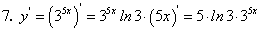 .
.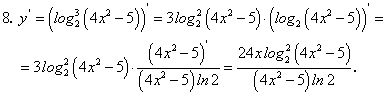
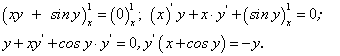
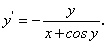
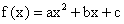 ;
;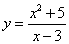 ;
;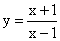 ;
;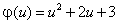 , вычислить
, вычислить 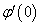 ;
;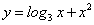 ;
;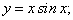
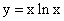 ;
;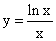 ;
;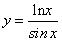 ;
;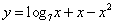 ;
;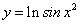 ;
;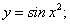
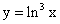 ;
;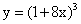 ;
;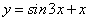 ;
;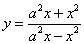 ;
;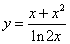 ;
;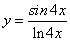 ;
;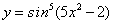 ;
;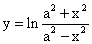 .
.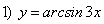 ;
;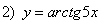 ;
;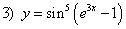 ;
;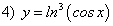 ;
;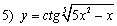 ;
;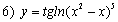 ;
;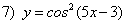 ;
;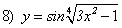 ;
;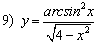 ;
;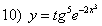 ;
;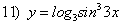 ;
;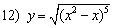 .
.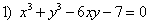 ;
;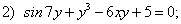
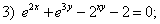
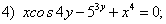
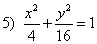 ;
;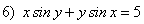 .
. функций, заданных параметрически:
функций, заданных параметрически: