Сегодня вы изучите вопросы
-
Предел последовательности
-
Свойства последовательностей, имеющих предел
-
Признаки существования предела
-
Бесконечно малая величина
-
Свойства бесконечно малых величин
-
Бесконечно большие величины и их связь с бесконечно малыми величинами
-
Основные теоремы о пределах.
-
Неопределенности
Изучив тему занятия, вы сможете
-
определить, какая величина бесконечно малая, а какая — бесконечно большая;
-
найти пределы переменных величин;
-
раскрыть неопределенности.
Основные понятия
В повседневной жизни мы часто употребляем термин «предел», не углубляясь в его сущность. В нашем представлении чаще всего предел отождествляется с понятием «ограниченность». В частности, крайние положения стрелок на панели автомобилей и других приборов характеризуют их предельное положение.
Приведем наглядный пример. Пусть требуется найти длину окружности.
Поставим перед собой вопрос: что можно принять за длину окружности? Естественным является желание выразить длину окружности через периметры фигур, которые мы в состоянии вычислить. Например, периметры правильных многоугольников, вписанных в окружность.
Простейшим является квадрат, вписанный в эту окружность. Очевидно, периметр квадрата является плохим приближением длины окружности. Для более точного приближения впишем в окружность правильный восьмиугольник (рис. 1.1 ).
).
Естественно, если этот процесс продолжить до бесконечности, то мы все точнее и точнее будем приближаться к длине окружности.
Все это наталкивает на мысль, что периметры правильных многоугольников, вписанных в окружность, при бесконечном удвоении числа их сторон стремятся к длине окружности, то есть длина окружности является пределом для этих периметров.
Изучаемый вами курс включает множество понятий, основанных на понятии предела. Сюда можно отнести площадь криволинейных фигур, площадь криволинейных поверхностей, объемы тел, кривизну линии, плотность неоднородного тела, предельные издержки, центр тяжести фигур и т.п.
Дадим вначале понятие предела для дискретных значений переменной величины, имеющих специальное наименование — «числовая последовательность».
Если по некоторому закону каждому натуральному числу n поставлено в соответствие действительное число хn, то множество действительных чисел х1, х2, …, хn, … называется числовой последовательностью , или просто последовательностью
, или просто последовательностью . Сокращенно последовательность обозначается символом {хn}.
. Сокращенно последовательность обозначается символом {хn}.
Числа х1, х2,…, хn называются элементами числовой последовательности , а число хn называется общим (или n-ым) членом этой последовательности. Если за хn принять значение функции f(x) при х = n, то числовую последовательность {хn} можно рассматривать как функцию натурального аргумента
, а число хn называется общим (или n-ым) членом этой последовательности. Если за хn принять значение функции f(x) при х = n, то числовую последовательность {хn} можно рассматривать как функцию натурального аргумента : хn = f(n).
: хn = f(n).
На практике чаще всего последовательность задается общим членом, с помощью которого можно найти значение любого члена этой последовательности.
Так, равенства vn = n2 — 1, zn = (-1)n ∙ n, 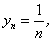
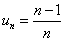 задают соответственно числовые последовательности:
задают соответственно числовые последовательности:
Заметим, что с возрастанием n значения первых двух числовых последовательностей стремятся к бесконечности, а значения последних двух — к определенным пределам (к нулю и единице соответственно). В соответствии с этим последовательности делятся на ограниченные и неограниченные.
Последовательность 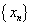 называется ограниченной
называется ограниченной , если существует такое число
, если существует такое число 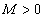 , что для любого n ϵ N выполняется неравенство
, что для любого n ϵ N выполняется неравенство 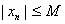 . В противном случае, когда
. В противном случае, когда 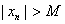 , последовательность называется неограниченной
, последовательность называется неограниченной . Легко заметить, что две последние последовательности
. Легко заметить, что две последние последовательности 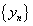 и
и 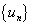 ограниченны, а первые две последовательности
ограниченны, а первые две последовательности 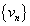 и
и 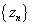 неограниченны.
неограниченны.
Пояснение понятия «предел числовой последовательности» начнем с рассмотрения простейшей числовой последовательности:
Придавая n последовательно значения 1, 2, 3 и т.д., мы получим числовую последовательность:
Заметим, что члены последовательности (2) с увеличением порядкового номера члена увеличиваются по величине, оставаясь меньше единицы. Причем разность между числом 1 и членами последовательности (2) с увеличением порядкового номера может быть меньше любого наперед заданного числа.
Для доказательства сделанного утверждения найдем значения сотого (f (100)) и сто первого (f (101)) членов:
Найдем модуль разности между найденными значениями и единицей:
Из курса геометрии нам известно, что расстояние d между двумя точками А(х1) и В(х2) числовой оси Ох равно модулю разности 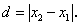 Отсюда заключаем, что расстояние между 101-м членом и единицей меньше, чем расстояние от 100-го члена до единицы, так как
Отсюда заключаем, что расстояние между 101-м членом и единицей меньше, чем расстояние от 100-го члена до единицы, так как 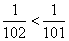 . Очевидно, с ростом порядкового номера n расстояние от единицы до члена последовательности (2) становится все меньше и меньше и может быть меньше любого наперед заданного сколь угодно малого положительного числа ε.
. Очевидно, с ростом порядкового номера n расстояние от единицы до члена последовательности (2) становится все меньше и меньше и может быть меньше любого наперед заданного сколь угодно малого положительного числа ε.
Действительно, задавшись наперед числом ε, найдем номер члена последовательности (2), начиная с которого для всех последующих членов этой последовательности выполняется неравенство:
Так как 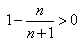 , то
, то 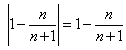 и неравенство (3) равносильно:
и неравенство (3) равносильно:
Решив числовое неравенство (4) относительно n, находим, что:
Таким образом, мы нашли, каким должно быть n по заданному ε, чтобы выполнялось неравенство (3).
Если, например, ε = 0,01, тогда из неравенства (5) следует, что номер члена последовательности 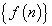 должен превосходить число
должен превосходить число 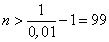 , т.е. начиная с сотого члена расстояние между единицей и членом последовательности (2) будет меньше, чем ε = 0,01. Если же ε = 0,001, то из (5) следует, что n > 999, т.е. начиная с тысячного члена расстояние между членами последовательности и единицей будет меньше, чем 0,001.
, т.е. начиная с сотого члена расстояние между единицей и членом последовательности (2) будет меньше, чем ε = 0,01. Если же ε = 0,001, то из (5) следует, что n > 999, т.е. начиная с тысячного члена расстояние между членами последовательности и единицей будет меньше, чем 0,001.
Из неравенства (5) и приведенного примера следует, что номер члена, для которого должно выполняться неравенство (3), зависит от числа ε: Чем меньше число ε, тем больше должен быть порядковый номер члена последовательности (2).
Далее имеем, что расстояние между членами последовательности (2) и ее пределом — единицей при n → ∞ становится меньше любого наперед заданного положительного числа, т.е. стремится к нулю.
Так как расстояние между двумя точками А(x1) и В(x2) числовой оси определяется разностью |x2 — x1|, то стремление членов последовательности (2) к своему пределу, равному единице, при неограниченном увеличении их порядкового номера n можно перефразировать следующим образом: члены последовательности (2) при n → ∞ стремятся к 1, т.к. расстояние между членами последовательности (2) и числом 1 стремится к нулю при n → ∞. Или: каково бы ни было наперед заданное сколь угодно малое положительное число ε, всегда найдется такой член последовательности (2), начиная с которого для всех последующих членов последовательности будет выполняться неравенство 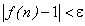 .
.
Более строго данный результат формулируется так: числовая последовательность 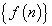 при n → ∞ имеет своим пределом число 1, т.к. для любого наперед заданного положительного числа ε всегда найдется такой член последовательности
при n → ∞ имеет своим пределом число 1, т.к. для любого наперед заданного положительного числа ε всегда найдется такой член последовательности 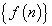 , начиная с которого для всех последующих членов этой последовательности выполняется неравенство
, начиная с которого для всех последующих членов этой последовательности выполняется неравенство 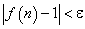 .
.
Дадим определение предела произвольной числовой последовательности.
Число a называется пределом числовой последовательности
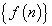 , если для любого сколь угодно малого наперед заданного положительного числа ε > 0 существует такой номер N, что для всех членов последовательности, для которых n > N, выполняется неравенство:
, если для любого сколь угодно малого наперед заданного положительного числа ε > 0 существует такой номер N, что для всех членов последовательности, для которых n > N, выполняется неравенство:
Это факт записывается так:
Символ lim образован от латинского слова «предел» (limes).
Из неравенства (6) следует, что -ε < f(n) — a < ε, или:
а — ε < f(n) < a + ε. (8)
Если значениям числовой последовательности 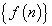 сопоставлять точки числовой оси (рис 1.2
сопоставлять точки числовой оси (рис 1.2 ), то из неравенства (8) следует, что все члены числовой последовательности
), то из неравенства (8) следует, что все члены числовой последовательности 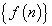 , для которых n > N, будут находиться внутри интервала (а — ε, а + ε).
, для которых n > N, будут находиться внутри интервала (а — ε, а + ε).
Здесь важно заметить, что внутри указанного интервала находится бесконечное число членов последовательности, а вне интервала — только конечное число членов. Это обстоятельство играет важную роль в обосновании основных положений теории пределов.
Как легко заметить, в принятых обозначениях нами отождествлены следующие понятия:
|f(n) — a |< ε и |xn — a |< ε.
Указанное выше отождествление приводит к следующему определению предела для числовой последовательности 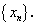
Число а называется пределом числовой последовательности
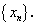 , если для любого сколь угодно малого наперед заданного положительного числа ε > 0 существует такой номер N, что для всех членов последовательности
, если для любого сколь угодно малого наперед заданного положительного числа ε > 0 существует такой номер N, что для всех членов последовательности 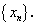 , для которых n > N, выполняется неравенство |xn — a| < ε.
, для которых n > N, выполняется неравенство |xn — a| < ε.
При рассмотрении последовательности (2), общий член которой был равен 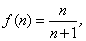 мы убедились, что для любого наперед заданного сколь угодно малого ε > 0 всегда можно найти такой номер N, что при n > N всегда выполняется неравенство
мы убедились, что для любого наперед заданного сколь угодно малого ε > 0 всегда можно найти такой номер N, что при n > N всегда выполняется неравенство 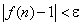 .
.
Из данного нами определения предела числовой последовательности вытекает, что 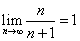 .
.
Определим, что понимается под пределом переменной x, когда значения х сплошь покрывают конечный или бесконечный промежуток.
Число а называется пределом действительной переменной величины х, если для любого сколь угодно малого наперед заданного положительного числа ε > 0 существует такое значение х, начиная с которого для всех остальных значений x выполняется неравенство |х — а| < ε.
х, если для любого сколь угодно малого наперед заданного положительного числа ε > 0 существует такое значение х, начиная с которого для всех остальных значений x выполняется неравенство |х — а| < ε.
Символически это записывается так: 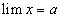 .
.
Из определения предела переменной величины х следует, что начиная с некоторого значения для всех остальных значений х выполняются неравенства -ε < x — a < ε или a — ε < x < a + ε, т.е. все эти остальные значения х находятся в ε — окрестности точки а (рис. 1.2):
(a — ε, a + ε).
Рассмотрим числовую последовательность, общий член которой определяется по формуле:
Очевидно, данная последовательность имеет предел, равный единице:
Действительно, для любого ε > 0 можно найти такое N, что для всех n > N будет выполняться неравенство 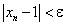 , или:
, или:
Отсюда находим искомое N из неравенства 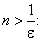
Таким образом, для всех n, для которых выполняется условие n > N, выполняется неравенство:
Рассмотрим числовую последовательность, общий член которой равен 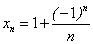 .
.
По аналогии можно доказать, что 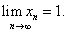
Заметим, что последовательность 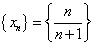 имеет предел, равный 1; члены последовательности принимают значения, меньшие своего предела; последовательность с общим членом
имеет предел, равный 1; члены последовательности принимают значения, меньшие своего предела; последовательность с общим членом 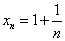 имеет своим пределом число 1, причем все члены этой последовательности принимают значения, большие 1; последовательность с общим членом
имеет своим пределом число 1, причем все члены этой последовательности принимают значения, большие 1; последовательность с общим членом 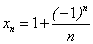 имеет предел, равный 1, причем члены последовательности принимают значения поочередно (то больше предела, то меньше предела). То есть члены первой числовой последовательности стремятся к своему пределу только слева, члены второй числовой последовательности стремятся к своему пределу только справа. Члены последней числовой последовательности стремятся к своему пределу одновременно и слева, и справа.
имеет предел, равный 1, причем члены последовательности принимают значения поочередно (то больше предела, то меньше предела). То есть члены первой числовой последовательности стремятся к своему пределу только слева, члены второй числовой последовательности стремятся к своему пределу только справа. Члены последней числовой последовательности стремятся к своему пределу одновременно и слева, и справа.
Таким образом, из определения предела последовательности переменной вытекает, что безразлично, как группируются значения членов вокруг своего предела.
Если же исследуется вопрос существования предела при стремлении переменной к своему пределу только с одной стороны (слева или справа), то речь идет о существовании так называемых односторонних пределов .
.
Символически они обозначаются так: xn → a — 0 (предел слева) и xn → a + 0 (предел справа).
В курсе математического анализа доказывается, что для существования предела необходимо и достаточно, чтобы существовали односторонние пределы, причем эти пределы должны быть равны между собой.
-
Если последовательность
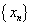 при n → ∞ имеет предел, равный a, и a > p (a < p), то все ее значения начиная с некоторого xN будут удовлетворять неравенству
при n → ∞ имеет предел, равный a, и a > p (a < p), то все ее значения начиная с некоторого xN будут удовлетворять неравенству 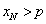
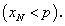
Следствие. По сформулированному свойству имеем: если p = 0 и а > 0, то для всех n > N будет выполняться неравенство xN > 0. Т.е. если предел переменной есть положительное число, то начиная с некоторого значения все оставшиеся члены последовательности будут положительными.
-
Если последовательность
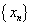 при n → ∞ имеет конечный предел, то эта последовательность ограничена и сверху, и снизу.
при n → ∞ имеет конечный предел, то эта последовательность ограничена и сверху, и снизу.Из определения предела последовательности следует, что предел постоянной величины есть эта постоянная величина.
Действительно, если рассмотреть последовательность, все члены которой равны а, то для произвольного ε > 0 выполняется неравенство |а — а| < ε для всех членов этой последовательности. Таким образом,
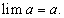
-
Последовательность
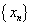 не может иметь двух различных пределов, т.е. если последовательность имеет предел, то этот предел единственный.
не может иметь двух различных пределов, т.е. если последовательность имеет предел, то этот предел единственный.Докажем теорему от противного. Пусть последовательность
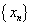 имеет два различных предела при n → ∞, например, a и b. Тогда, по определению предела последовательности, существуют такие
имеет два различных предела при n → ∞, например, a и b. Тогда, по определению предела последовательности, существуют такие 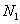 и
и 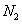 , что для всех n, для которых
, что для всех n, для которых 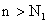 и
и 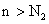 соответственно, при любом наперед заданном
соответственно, при любом наперед заданном 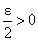 выполняются неравенства
выполняются неравенства 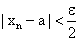 и
и 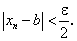
Из двух значений N1 и N2 выберем наибольшее значение, обозначим это значение через N. Тогда для всех
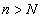 будут выполняться неравенства
будут выполняться неравенства 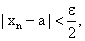
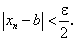
Возьмем модуль разности:
|a — b| = |xn — b + a — xn| ≤ |xn — a| + |xn — b| < ε.
Последнее неравенство возможно только в одном случае — когда a = b.
В предыдущем разделе мы изучили свойства последовательностей, имеющих предел. Естественным и главным является вопрос: когда последовательность имеет предел? В этом разделе излагаются основные теоремы существования предела.
Последовательность 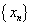 называется монотонно возрастающей
называется монотонно возрастающей , если из неравенства n > N следует строгое неравенство
, если из неравенства n > N следует строгое неравенство 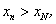 и монотонно убывающей
и монотонно убывающей — если
— если 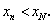
Теорема 1. Если последовательность 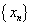 монотонно возрастающая (или убывающая) и ограничена сверху, например, числом M (или ограничена снизу числом m), то последовательность
монотонно возрастающая (или убывающая) и ограничена сверху, например, числом M (или ограничена снизу числом m), то последовательность 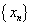 имеет предел, меньший или равный М (больший или равный m).
имеет предел, меньший или равный М (больший или равный m).
Теорема 2. Если последовательности 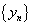 и
и 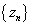 имеют один и тот же предел, а для членов последовательности
имеют один и тот же предел, а для членов последовательности 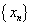 начиная с некоторого члена xN выполняются неравенства
начиная с некоторого члена xN выполняются неравенства
то последовательность 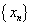 имеет тот же предел, что и
имеет тот же предел, что и 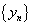 ,
, 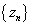 .
.
Все перечисленные свойства для числовой последовательности целиком можно перенести и на переменную величину x.
Среди множества переменных величин особое место занимают переменные величины, пределы которых равны нулю или бесконечности. К изучению этих переменных мы и перейдем.
Переменная величина x называется бесконечно малой величиной (б.м.в.), если она имеет своим пределом число нуль, или для любого наперед заданного сколь угодно малого положительного числа ε > 0 найдется такое значение x, начиная с которого для всех остальных ее значений будет выполняться неравенство
(б.м.в.), если она имеет своим пределом число нуль, или для любого наперед заданного сколь угодно малого положительного числа ε > 0 найдется такое значение x, начиная с которого для всех остальных ее значений будет выполняться неравенство 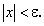
Здесь следует обратить внимание на то, что б.м.в. есть величина переменная. И только единственное постоянное число нуль можно отнести по сформулированному определению к б.м.в. Так, например, число 0,000000000000001 не является б.м.в.
Теорема 3. Алгебраическая сумма конечного числа б.м.в. есть величина бесконечно малая.
Под алгебраической суммой понимается сумма или разность выражений.
Доказательство проведем для трех б.м.в. Пусть α, β, γ — б.м.в., т.е.
Требуется доказать, что 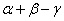 — бесконечно малая величина, т.е.
— бесконечно малая величина, т.е. 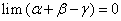 .
.
Доказательство. Так как α, β, γ — б.м.в., то по определению б.м.в. найдутся такие значения α, β, γ, начиная с которых, для всех остальных значений переменных α, β, γ и для любого наперед заданного 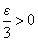 будут выполняться неравенства:
будут выполняться неравенства:
Отсюда на основании свойств модуля имеем:
Теорема 4. Произведение бесконечно малой величины на ограниченную переменную величину есть величина бесконечно малая.
Дано: α — б.м.в., x — ограниченная переменная величина, т.е. 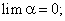 существует такое
существует такое 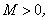 что для всех x выполняется неравенство
что для всех x выполняется неравенство 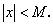
Требуется доказать, что 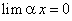 , или для произвольного сколь угодно малого ε > 0 выполняется неравенство
, или для произвольного сколь угодно малого ε > 0 выполняется неравенство 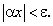
Доказательство. Так как α — б.м.в., то начиная с некоторого значения α для всех остальных ее значений выполняется неравенство 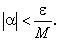 Отсюда находим:
Отсюда находим:
Следствие 1. Произведение бесконечно малой величины на постоянную величину есть величина бесконечно малая.
Действительно, так как любая постоянная величина есть величина ограниченная, то по теореме 4 справедливо указанное следствие.
Следствие 2. Произведение любого числа бесконечно малых величин есть величина бесконечно малая.
Действительно, так как б.м.в. есть величина ограниченная, то произведение двух б.м.в. — величина б.м.в. Умножив две б.м.в. на третью б.м.в. вновь получим б.м.в. и т.д.
Теорема 5. Если α — б.м.в., а переменная х имеет предел, отличный от нуля, то 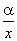 — б.м.в., т.е. частное от деления б.м.в. на переменную, имеющую предел, отличный от нуля, есть б.м.в.
— б.м.в., т.е. частное от деления б.м.в. на переменную, имеющую предел, отличный от нуля, есть б.м.в.
Переменная величина х называется бесконечно большой величиной (б.б.в.), если для любого наперед заданного сколь угодно большого числа
(б.б.в.), если для любого наперед заданного сколь угодно большого числа 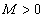 найдется такое значение переменной х, начиная с которого для всех остальных ее значений выполняется неравенство
найдется такое значение переменной х, начиная с которого для всех остальных ее значений выполняется неравенство 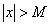 .
.
Символически этот факт записывается так: 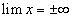 .
.
Например, если областью изменения переменной х является вся числовая ось, то, каково бы ни было значение 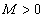 , которому соответствует фиксированная точка числовой оси, для всех остальных значений х, находящихся правее точки
, которому соответствует фиксированная точка числовой оси, для всех остальных значений х, находящихся правее точки 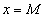 и левее т.
и левее т. 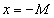 , будет выполняться неравенство
, будет выполняться неравенство 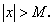
Очевидно, при 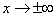 переменные
переменные 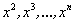 , а также их суммы, будут б.б.в.
, а также их суммы, будут б.б.в.
Теорема 6. Если α — б.м.в., а переменная х — б.б.в., то:
Теорема 7. Если переменная величина х имеет предел, равный действительному числу а, то начиная с некоторого значения х для всех остальных значений этой переменной будет выполняться равенство:
x = a + α, (10)
где α — б.м.в.
Доказательство. По определению предела, если 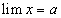 , то начиная с некоторого значения переменной х для всех ее остальных значений выполняется неравенство:
, то начиная с некоторого значения переменной х для всех ее остальных значений выполняется неравенство:
|х — а| < ε, (11)
где ε > 0 — наперед заданное сколь угодно малое положительное число.
Если разность x — a под знаком модуля в неравенстве (11) обозначить через α (т.е. x — a = α), то из неравенства (11) будет следовать по определению б.м.в., что α — б.м.в., так как из (11) будет следовать, что 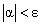 . Т.о. нами получено равенство: x — a = α, где α — б.м.в.
. Т.о. нами получено равенство: x — a = α, где α — б.м.в.
Отсюда окончательно находим: x = a + α.
Обратно, если имеет место равенство x = a + α, где α — б.м.в., то 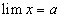 .
.
Действительно, по условию имеем: |х — а| = |α| < ε. По определению предела переменной отсюда находим, что 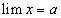 .
.
Условимся впредь под ε понимать наперед заданное сколь угодно малое положительное число.
Теорема 8. Предел алгебраической суммы конечного числа переменных величин, имеющих конечный предел, равен алгебраической сумме пределов слагаемых величин, т.е.
По условию теоремы дано:
По теореме 7 из равенств (13) следует, что:
x = a + α, y = b + β, z = c + γ, (14)
где α, β, γ — б.м.в.
Из равенств (14) имеем:
x + y — z = a + b — c + α + β — γ. (15)
Левая часть равенства (15) есть сумма переменных величин. Обозначим ее через 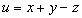 . Правая часть состоит из алгебраической суммы постоянных величин и суммы трех б.м.в. Обозначим алгебраическую сумму постоянных величин через
. Правая часть состоит из алгебраической суммы постоянных величин и суммы трех б.м.в. Обозначим алгебраическую сумму постоянных величин через 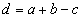 , а алгебраическую сумму б.м.в. — через
, а алгебраическую сумму б.м.в. — через 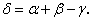 В этих обозначениях равенство (15) перепишется так:
В этих обозначениях равенство (15) перепишется так:
где d — постоянная величина,
δ — б.м.в. по доказанному ранее.
Следовательно, по обратной теореме 7 имеем:
или, с учетом равенств (13):
Теорема 9. Предел произведения конечного числа переменных величин, имеющих предел, равен произведению пределов этих величин, т.е. из существования конечных пределов 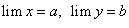 переменных х и у следует равенство:
переменных х и у следует равенство:
Доказательство можно провести аналогично доказательству теоремы 8.
Следствие 1. Постоянный множитель можно выносить за знак предела, если предел существует: 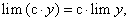 т.к.
т.к. 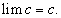
Следствие 2. Предел степени переменной, имеющей предел, равен той же степени от предела переменной, т.е. 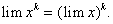
Следствие 3. Предел корня n-ой степени от переменной, имеющей предел, равен корню n-ой степени от предела этой переменной, т.е.
Действительно, пусть 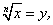 тогда по определению корня
тогда по определению корня 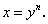
Из полученного равенства 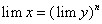 следует, что
следует, что 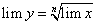 , или
, или 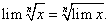
Теорема 10. Предел частного двух переменных величин равен отношению предела числителя на предел знаменателя, если эти пределы существуют и предел знаменателя отличен от нуля, т.е.
Доказательство можно провести по аналогии с приведенным доказательством теоремы 8 (рекомендуем читателю провести доказательство самостоятельно).
Следствие 1. Если 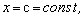 то
то 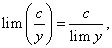 если
если 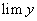 существует и отличен от нуля.
существует и отличен от нуля.
Следствие 2. Если 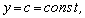 то
то 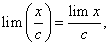 если
если 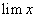 существует и
существует и 
Рассмотрим типовые примеры отыскания пределов переменных величин.
Числитель дроби есть переменная, предел которой можно найти, применяя теоремы о пределах и их следствия:
Найдем предел знаменателя:
Следовательно, по теореме 4 имеем:
Заметим, что данный предел зависит от того, с какой стороны переменная x → 1. Если переменная x → 1, оставаясь всегда меньше 1, то этот предел является левым односторонним пределом для точки x = 1. Если же переменная x → 1, оставаясь всегда больше 1, то этот предел является односторонним пределом справа в точке x = 1. Первый предел по определению обозначается символически так: 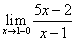 (или
(или 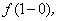 где
где 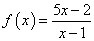 ); второй предел, называемый односторонним правым пределом, символически обозначается так:
); второй предел, называемый односторонним правым пределом, символически обозначается так:
Найдем односторонние пределы:
Мы видим, что односторонние пределы бесконечны, причем левый предел отличен от правого. Вывод: заданный предел не существует.
Рассмотрим несколько подробнее отношение дроби 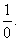 Оценим это отношение с точки зрения предела переменной.
Оценим это отношение с точки зрения предела переменной.
Рассмотрим дробь 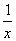 , когда x → 0.
, когда x → 0.
Найдем значения односторонних пределов: пусть x → 0 слева, т.е. оставаясь меньше нуля. Рассмотрим последовательность значений х, стремящихся к 0, оставаясь меньше нуля, например, значения: -0,1; -0,01; -0,001 и т.д. Значения рассматриваемой дроби в указанных точках соответственно будут равны -10; -100; -1000 и т.д., т.е. значение дроби стремится к -∞.
По аналогии, если взять значения х, стремящиеся к 0 справа от точки х = 0 (т.е. точки 0,1; 0,01; 0,001 и т.д.), то значениями дроби 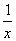 в указанных точках будут соответственно равны 10; 100; 1000 и т.д., т.е. значение дроби
в указанных точках будут соответственно равны 10; 100; 1000 и т.д., т.е. значение дроби 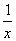 при x → 0 равно +∞. Этим и объясняются значения односторонних пределов в приведенном примере.
при x → 0 равно +∞. Этим и объясняются значения односторонних пределов в приведенном примере.
Рассмотрим случай, когда числитель и знаменатель дроби стремятся к нулю при стремлении х к фиксированной точке, например, к 1 или 2 и т.д.
В приведенном примере предел числителя существует и равен 0; предел знаменателя существует и тоже равен нулю. Значит, применить теорему о пределе частного нельзя. Однако если осуществить предельный переход после некоторых преобразований, то в некоторых случаях мы можем вычислить пределы отношения некоторых переменных величин. Такие пределы называются неопределенностями вида 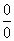 .
.
Для обозначения полученной неопределенности и других видов неопределенностей введем следующую символику: 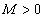 и т.д.
и т.д.
Пример 4. Найти предел:
Найдем пределы, содержащие иррациональные выражения.
Пример 5.
Пример 6.
Пример 7.
К неопределенностям относятся также отношения двух переменных, пределы которых стремятся к бесконечности при х, стремящемуся к конечному или бесконечному пределу.
Числитель и знаменатель заданной дроби, каждый в отдельности, стремятся к бесконечности. Однако предел заданного отношения есть конкретная величина. Действительно, разделив числитель и знаменатель заданной дроби на х3, получим:
Пример 9. Найти предел:
Данный предел также представляет неопределенность вида 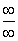 . Для вычисления указанного предела разделим числитель и знаменатель заданной дроби на х2:
. Для вычисления указанного предела разделим числитель и знаменатель заданной дроби на х2:
К неопределенностям также относятся пределы от разности функций 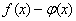 , каждая из которых стремится к бесконечности при стремлении х к конечному или бесконечному пределу.
, каждая из которых стремится к бесконечности при стремлении х к конечному или бесконечному пределу.
Предел числителя полученной дроби есть конечное число, а предел знаменателя равен нулю. Вывод: данный предел не существует.
Решим вопросы существования односторонних пределов:
Пример 11. Найти предел:
К неопределенностям также относятся пределы от функции 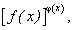 где пределы функций f(x) и φ(x), когда х стремится к конечному или бесконечному пределу, равны соответственно 1 и ∞; ∞ и 0; 0 и 0: 1∞; ∞0; 00; 0∞.
где пределы функций f(x) и φ(x), когда х стремится к конечному или бесконечному пределу, равны соответственно 1 и ∞; ∞ и 0; 0 и 0: 1∞; ∞0; 00; 0∞.
Контрольные вопросы
-
Что называется последовательностью?
-
Какая последовательность называется возрастающей (убывающей)?
-
Какая последовательность называется ограниченной? Приведите примеры.
-
Что называется пределом последовательности?
-
Сколько пределов может иметь последовательность?
-
Сформулируйте необходимое условие существования предела последовательности.
-
Какая последовательность называется бесконечно большой? Приведите примеры.
-
Какая последовательность называется бесконечно малой? Приведите примеры.
-
Сформулируйте основные теоремы о пределах.
-
Назовите основные виды неопределенностей.
Задания для самостоятельной работы
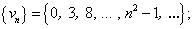
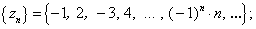
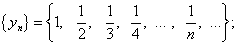
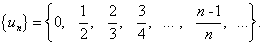
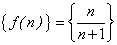 . (1)
. (1)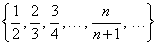 . (2)
. (2)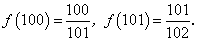
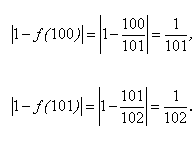
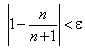 . (3)
. (3)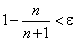 . (4)
. (4)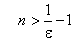 . (5)
. (5)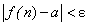 . (6)
. (6)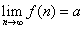 (7)
(7)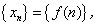
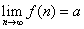 и
и 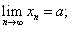
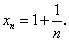
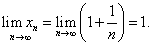
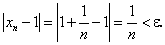
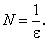
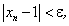 т.е.
т.е. 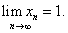
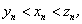 (9)
(9)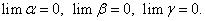
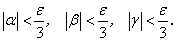
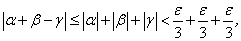 или
или 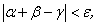 ч.т.д.
ч.т.д.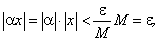 ч.т.д.
ч.т.д. — б.м.в.;
— б.м.в.;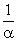 — б.б.в.;
— б.б.в.;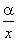 — б.м.в.
— б.м.в.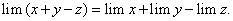 (12)
(12)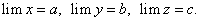 (13)
(13)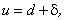
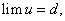 или
или 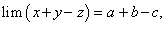
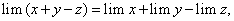 ч.т.д.
ч.т.д.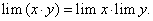
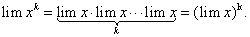
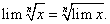
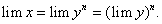
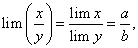 если
если 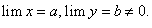
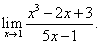
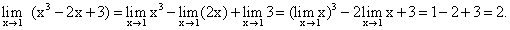
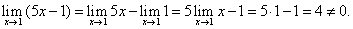
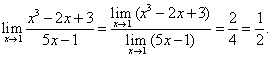
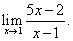
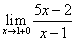 (или
(или 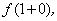 где
где 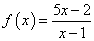 ).
).
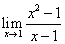 .
.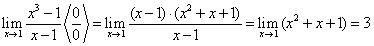 .
.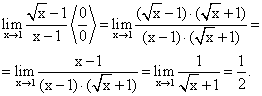
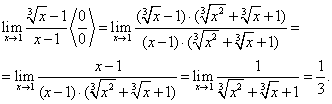
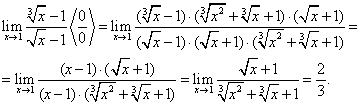
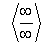 .
.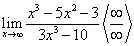 .
.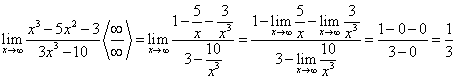 .
.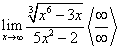 .
.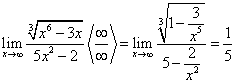 .
.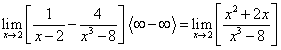 .
.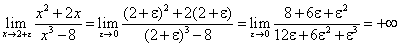 ;
;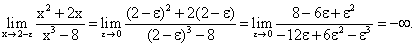
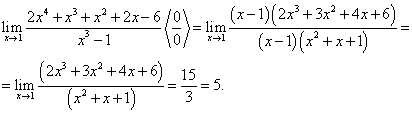
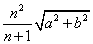 ;
;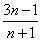 ;
;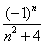 ;
;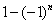 .
.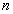 -го члена:
-го члена: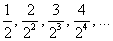
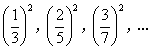
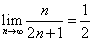 ;
;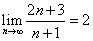 ;
;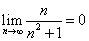 ;
;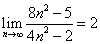 ;
;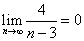 ;
;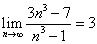 .
.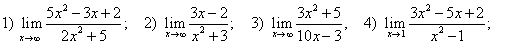
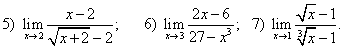
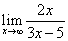 ;
;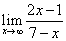 ;
;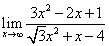 ;
;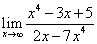 ;
;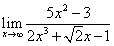 ;
;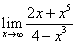 ;
;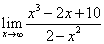 ;
;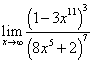 ;
;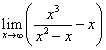 ;
;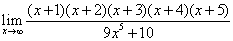 ;
;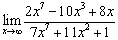 ;
;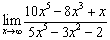 ;
;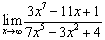 ;
;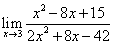 ;
;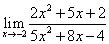 ;
;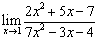
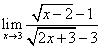 ;
;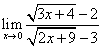 ;
;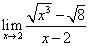 ;
;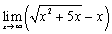 ;
;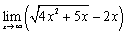 ;
;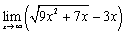 .
.
