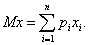Успешно изучив материал, Вы будете знать:
-
понятие случайного события;
-
вероятность случайных событий;
-
сложные и простые события;
-
вероятность сложного события;
-
понятие распределения вероятности;
-
понятие среднего значение случайной величины;
-
понятие дисперсии случайной величины;
-
понятие выборки.
После изучения данной темы Вы будете уметь:
-
рассчитать вероятность последовательности случайных событий;
-
вычислять среднее значение непрерывного распределения.
После изучения материала Вы будете обладать навыками расчета вероятности в простых случаях.
Распределение случайной величины
Событием называется всякий факт, который может произойти или не произойти в результате опыта. При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда. В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом — нет.
называется всякий факт, который может произойти или не произойти в результате опыта. При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда. В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом — нет.
События называются несовместными , если появление одного из них исключает появление других.
, если появление одного из них исключает появление других.
Полной группой событий называется совокупность всех возможных результатов опыта.
называется совокупность всех возможных результатов опыта.
Классическим примером несовместных событий является результат подбрасывания монеты — выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).
Достоверным называется событие, которое наверняка произойдет в результате опыта.
называется событие, которое наверняка произойдет в результате опыта.
Событие называется невозможным , если оно никогда не произойдет в результате опыта.
, если оно никогда не произойдет в результате опыта.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого — невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А, к общему числу опытов.
называется отношение числа опытов, в результате которых произошло событие А, к общему числу опытов.
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события .
.
Вообще говоря, классическое определение вероятности — довольно относительное. Это обусловлено тем, что на практике сложно представить результат опыта в виде совокупности элементарных событий и доказать, что события равновероятные.
К примеру, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы, как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д.
Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов. Чтобы преодолеть этот недостаток, вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой-либо отрезок или часть плоскости (пространства).
Так, если на отрезке длиной L выделен отрезок длины l, то вероятность попадания наугад взятой точки в отрезок равна отношению l / L.
События называются равновозможными , если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
В приведенном выше примере с шарами в коробке появление красного и зеленого шаров — равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров. Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара — событие менее вероятное, чем появление красного. Исходя из этих общих понятий можно дать определение вероятности.
Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта.
называется математическая оценка возможности появления этого события в результате опыта.
Вероятность события А равна отношению числа благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.
Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного — равна нулю. Таким образом, значение вероятности любого события — есть положительное число, заключенное между нулем и единицей.
Пример.
В коробке находится 10 шаров. 3 из них красные, 2 — зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет заданного цвета.
Решение. Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара — событием А, появление зеленого — событием В, появление белого — событиме С. Тогда в соответствием с записанными выше формулами получаем:
р(А) = 3 / 10; р(В) = 2 / 10; р(С) = 5 / 10.
Всего равновероятных исходов 10 (общее число шаров), причем все эти события несовместные. Благоприятный исход события А — вынут красный шар — возможен в трех из 10 случаях (красных шаров 3). Аналогично находим вероятности р(В) и р(С).
Вспомним основные правила комбинаторики.
-
Правило суммы.
Если два действия взаимоисключают друг друга, причем одно из них можно выполнить m способами, а другое — n способами, то выполнить одно любое из этих действий можно N = n + m способами.
-
Правило умножения.
Пусть требуется выполнить одно за другим какие-то два действия. Если первое действие можно выполнить n способами, после этого второе действие можно осуществить m способами, то оба действия могут быть выполнены m × n способами.
Отсюда следует, что:
-
вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий;
-
вероятность наступления последовательно нескольких несовместных событий равна произведению вероятностей этих событий.
Пример 1.
В коробке находится 10 шаров. 3 из них красные, 2 — зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет цветной. Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара — событие А, появление зеленого — событие В, появление белого — событие С. Тогда в соответствием с записанными выше формулами получаем:
р(А V B) = р(A) + р(В) = 3 / 10 + 2 / 10 = 5 / 10.
Пример 2.
Двое кидают 2 кубика. Первый выиграет, если хотя бы на одном выпадет «6», а второй — если на обоих кубиках будут четные. У кого вероятность выиграть выше?
Решение примера.
р1 = р(«6» V «6») = 1/6 +1/6 = 1/3, аналогично предыдущему примеру.
Во втором случае должны произойти последовательно два независимых события: на одном выпало четное число и на другом тоже выпало четное число.
Каждое событие выпадения четного числа, в свою очередь, является результатом появления любого из нескольких возможных событий.
р2 = р(четн Λ четн.) = р(«2» V «4» V «6») × р(«2» V «4» V «6») = (1/6 + 1/6 +1/6) × (1/6 + 1/6 +1/6) = 1/2 × 1/2 = 1/4.
р1 > р2.
Пример 3.
Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25 %, второй завод — 35 % и третий — 40 % всей производимой продукции. Брак составляет 5 % от продукции первого завода, 3 % от продукции второго и 4 % от продукции третьего завода. Вся продукция смешивается и поступает в продажу.
Найти:
а) вероятность купить бракованное изделие;
б) условную вероятность того, что купленное изделие изготовлено первым заводом, если это изделие бракованное.
Первая вероятность равна доле бракованных изделий в объеме всей продукции, т.е. 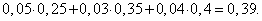 Вторая вероятность равна доле брака первого завода среди всего брака, т.е.
Вторая вероятность равна доле брака первого завода среди всего брака, т.е. 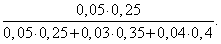
Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента — случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, — случайная величина. Случайная величина является одним из центральных понятий теории вероятностей.
Случайной величиной является, например, число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M = {1, 2, 3, 4, 5, 6}; во втором случае — с непрерывной случайной величиной (она принимает значения из непрерывного числового множества — из промежутка числовой прямой I = [100, 3000]).
Каждая случайная величина полностью определяется своей функцией распределения .
.
Если X — случайная величина, то функция F(x) = Р(X ≤ x) называется функцией распределения случайной величины X. Здесь Р(X ≤ x) — вероятность того, что случайная величина X принимает значение, меньшее или равное x.
Важно понимать, что функция распределения является «паспортом» случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения определена на всей числовой прямой. Очевидно, что F(-∞) = 0, F(+∞) = 1.
Действительно, F(+∞) — вероятность того, что случайная величина примет хоть какое-то значение.
Если x — дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями р1 < р2 < … < рi < …, то таблица 20.1 называется распределением дискретной случайной величины .
.
Таблица 20.1.
Распределение дискретной случайной величины
| x1 |
x2 |
x3 |
… |
xN |
р1 |
р2 |
р3 |
… |
рN |
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости , распределение, функция распределения и график функции распределения имеют следующий вид (рис. 20.1 ).
).
Каждая случайная величина полностью определяется своей функцией распределения. В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся, в первую очередь, математическое ожидание и дисперсия.
Математическое ожидание — число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx или μ.
— число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx или μ.
Математическое ожидание дискретной случайной величины x , имеющей распределение:
x1 |
x2 |
... |
xn |
р1 |
р2 |
... |
рn |
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания. Дисперсия обозначается Dx или σ2 .
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x — Mx)2 или Dx = M(x — Mx)2 = Mx2 — M(x)2
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных.
Иногда вместо дисперсии используют среднеквадратичное отклонение
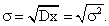
Нормальное распределение , также называемое распределением Гаусса
, также называемое распределением Гаусса , — распределение вероятностей, которое играет важнейшую роль во многих областях знаний: в физике, социологии, биологии. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний: в физике, социологии, биологии. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством.
Значения параметров соответствуют значениям среднего (математического ожидания μ) и разброса (стандартного отклонения σ2
) (рис. 20.2 ).
).
Среднее значение характеризует наиболее вероятное значение случайной величины. Разброс характеризует, насколько сильно отличаются ее значения от среднего.
характеризует наиболее вероятное значение случайной величины. Разброс характеризует, насколько сильно отличаются ее значения от среднего.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определенной процедуры выбранных из генеральной совокупности для участия в исследовании.
— множество случаев (испытуемых, объектов, событий, образцов), с помощью определенной процедуры выбранных из генеральной совокупности для участия в исследовании.
Репрезентативность выборки — условие, при котором среднее значение и дисперсия выборки совпадают со значениям генеральной совокупности.
— условие, при котором среднее значение и дисперсия выборки совпадают со значениям генеральной совокупности.
Репрезентативные выборки используют в социологических исследованиях, проверке качества изделия и пр.
используют в социологических исследованиях, проверке качества изделия и пр.
Основные выводы
-
Событием
 называется всякий факт, который может произойти или не произойти в результате опыта. При этом тот или иной результат опыта может быть получен с различной степенью возможности. События называются несовместными, если появление одного из них исключает появление других.
называется всякий факт, который может произойти или не произойти в результате опыта. При этом тот или иной результат опыта может быть получен с различной степенью возможности. События называются несовместными, если появление одного из них исключает появление других. -
Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А, к общему числу опытов. При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.
-
Для решения задач следует запомнить правила
-
вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.
-
вероятность наступления последовательно нескольких несовместных событий равна произведению вероятностей этих событий.
-
-
Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, — случайная величина. Случайная величина является одним из центральных понятий теории вероятностей. Случайной величиной является, например, число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M = {1, 2, 3, 4, 5, 6}; во втором случае — с непрерывной случайной величиной (она принимает значения из непрерывного числового множества — из промежутка числовой прямой I = [100, 3000]).
-
Каждая случайная величина полностью определяется своей функцией распределения. Если X — случайная величина, то функция F(x) = Р(X ≤ x) называется функцией распределения случайной величины X. Здесь Р(X ≤ x) — вероятность того, что случайная величина X принимает значение, меньшее или равное x.
-
Математическое ожидание
 — число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx или μ.
— число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx или μ. -
Нормальное распределение
 , также называемое распределением Гаусса
, также называемое распределением Гаусса , — распределение вероятностей, которое играет важнейшую роль во многих областях знаний: в физике, социологии, биологии. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех.
, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний: в физике, социологии, биологии. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. -
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством.
-
Выборка
 — множество случаев (испытуемых, объектов, событий, образцов), с помощью определенной процедуры выбранных из генеральной совокупности для участия в исследовании. Репрезентативность выборки — условие, при котором среднее значение и дисперсия выборки совпадают со значениям генеральной совокупности. Репрезентативные выборки используют в социологических исследованиях, проверке качества изделия и пр.
— множество случаев (испытуемых, объектов, событий, образцов), с помощью определенной процедуры выбранных из генеральной совокупности для участия в исследовании. Репрезентативность выборки — условие, при котором среднее значение и дисперсия выборки совпадают со значениям генеральной совокупности. Репрезентативные выборки используют в социологических исследованиях, проверке качества изделия и пр.
Контрольные вопросы
-
Какие события можно считать случайными?
-
Что такое вероятность случайного события?
-
Какие события можно считать независимыми?
-
Как рассчитать вероятность последовательности независимых событий?
-
Что такое распределение вероятности?
-
Подумайте, в каких случаях результаты выборочных испытаний не соответствуют всей генеральной совокупности.
Интернет-источники
Задания для самостоятельной работы
Выполните задания к теме 20 в тетради-практикуме.