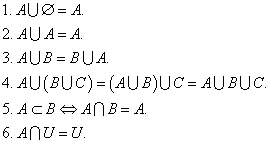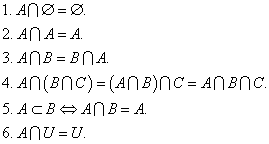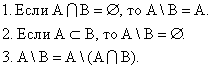Успешно изучив материал, Вы будете знать:

• понятие множества;

• основные операции над множествами (пересечение, объединение дополнение);

• понятие размерности множества;

• конечные, бесконечные, пустые множества;

• бинарные отношения;

• свойства бинарных отношений;

• понятие графа;

• представление графов;

• классификацию графов.

После изучения данной темы Вы будете уметь:

• выделять множества;

• сравнивать размерности множеств;

• выполнять операции над множествами;

• решать простейшие задачи теории множеств;

• формулировать задачи на языке теории множеств;

• описывать бинарные отношения между объектами;

• классифицировать графы;

• описывать простейшие системы с помощью графов.

После изучения материала Вы будете обладать навыками:

• формализации задач с помощью языка теории множеств;

• использования теоретико-множественных обозначений;

• описания бинарных отношений между элементами множеств.

Множество

Элемент множества

Размерность множества

Пересечение (И)

Объединение (ИЛИ)

Разность (КРОМЕ)

Размерность

Отношение

Вершина и ребро графа

Степень вершины

Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество. Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия.

1. Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.

2. Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).

Множества обычно обозначаются заглавными латинскими буквами. Если элемент x принадлежит множеству A, то это обозначается: x ϵ A

Термин «множество» в математике не всегда обозначает большое количество предметов, оно может состоять и из одного элемента и вообще не содержать элементов, тогда его называют пустым и обозначают Ø.

Если каждый элемент множества B является также и элементом множества A, то говорят, что множество B является подмножеством множества A (рис. 17.1): .

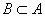Подмножество B множества A называется собственным подмножеством, если B ≠ A.

Используя понятие множества можно построить более сложные и содержательные объекты.

Размерность множества — количество входящих в него элементов.

Множества разделяют на конечные и бесконечные.

Например, множество всех целых чисел — бесконечное.

Размерность множества целых положительных чисел, меньших 100, равна 99.

Множество живых динозавров на Земле — пустое.

Основными операциями над множествами являются объединение, пересечение и разность.

Объединением двух множеств называется новое множество, элементы которого принадлежат хотя бы одному из этих множеств (рис. 17.2):

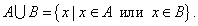
Отметим разницу в употреблении союза «или» в математике и в обыденной речи. В обыденной речи союз «или» употребляется чаще в разделительном смысле — «либо…, либо», тогда как в математике — в объединительном.

Свойства объединения множеств:

Пересечением двух множеств называется новое множество (рис. 17.3):

Разностью двух множеств называется новое множество (рис. 17.4):

Свойства пересечения множеств:

Если класс объектов, на которых определяются различные множества, обозначить Ω(Универсум), то дополнением множества A называют разность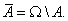

Свойства разности множеств:

Например, пусть А — множество всех студентов МФПА. В — множество всех работающих. Тогда пересечение А и В содержит всех работающих студентов МФПА.

В математике отношение определяет некоторую связь между двумя предметами (объектами). В идеальном мире (существующем в сознании людей) и в реальном (физическом) мире существуют разнообразные отношения между предметами. Поэтому математики и специалисты в области компьютеров используют множество различных бинарных (двуместных) отношений. Бинарные отношения могут иметь имена, например «равенство», «отношение порядка» и т.п. Некоторые из бинарных отношений помимо имен имеют стандартные символьные обозначения. Примерами таких отношений являются «равенство» (стандартное обозначение =), отношения «больше, (>)» и «меньше, (<)» и ряд других отношений.

Кроме бинарных существуют n-арные отношения, но они, в отличие от бинарных отношений, не имеют общего символьного обозначения. Заметим, что n-арные отношения широко используются в теории реляционных баз данных.

Любое бинарные отношение представляется множеством упорядоченных пар элементов. В математике множество элементов обозначается с помощью двух фигурных скобок { }, а упорядоченная пара — с помощью символов < >. Множество {<2,4>, <7,3>, <3,3>}, будучи множеством, состоящим из трех упорядоченных пар, есть бинарное отношение. Пара <2,4> является элементом этого бинарного отношения. Элемент бинарного отношения, т.е. упорядоченную пару, в общем случае обозначим <x1,x2>. Элементы в упорядоченной паре нельзя менять местами и, наоборот, элементы множества можно менять местами и при этом множество не меняется, т.е. два множества с одинаковыми, но по-разному расположенными элементами равны. Например {1,2}={2,1}.

В качестве примера бинарного отношения рассмотрим все упорядоченные пары элементов, которые можно составить на множестве {1,2}. Для множества {1,2} путем перестановки его элементов можно составить всего лишь две упорядоченные пары <1,2> и <2,1>. Набор из двух упорядоченных пар <1,2>, <2,1> является примером бинарного отношения, установленного на множестве двух элементов {1,2}. Если множество состоит из трех элементов, то самое большое бинарное отношение, которое можно построить на нем, состоит из 6-ти упорядоченных пар. Подмножество этого бинарного отношения может состоять, например, только из 3-х упорядоченных пар. Очевидно, что для множества из n элементов самое большое (полное) бинарное отношение будет состоять из Сn = n(n-1) упорядоченных пар. Эти математические рассуждения пригодятся нам при рассмотрении теории графов.

Поскольку бинарные отношения постоянно встречаются в математике и науке о компьютерах, то часто прилагательное «бинарное» опускается и вместо словосочетания «бинарное отношение» говорят просто «отношение».

Рассмотрим теперь бинарные отношения, записываемые не в числовом виде, а с помощью слов. Пусть имеется множество, состоящее из двух словесных элементов {«отец-Иван», «сын Ивана-Николай»}. Установленное на нем полное бинарное отношение состоит из двух упорядоченных пар — <отец-Иван, сын-Николай> и <сын-Николай, отец-Иван>. Поименованные бинарные отношения используются в реляционных базах данных.

Математики рассматривают отношения с двух точек зрения. Иногда они смотрят на отношения как на самостоятельные объекты, в других случаях — используют отношения совместно с множествами элементов, на которых эти отношения устанавливаются.

Граф G — это совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами.

На рис. 17.5 слева изображен граф, имеющий пять вершин и шесть ребер. Если рассматривается множество упорядоченных пар точек, т.е. на каждом ребре задается направление, то граф G называется ориентированным. В противном случае G называется неориентированным графом.

Степенью вершины называется число ребер, которым принадлежит вершина.

Методы теории графов позволяют найти кратчайший путь между двумя вершинами, способы обхода вершин без возврата и т.п.

Закономерность 1. Число нечетных вершин любого графа четно.

Закономерность 2. Невозможно начертить граф с нечетным числом нечетных вершин.

Закономерность 3. Если все вершины графа четные, то можно начертить этот граф, не отрывая карандаш от бумаги, («одним росчерком»), проводя по каждому ребру только один раз. Движение можно начать с любой вершины и закончить его в той же вершине.

Закономерность 4. Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.

Закономерность 5. Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».

С помощью графов часто упрощается решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети, маршрутизация в сети. Помогают графы в решении математических и экономических задач.

Рассмотрим пример. Для расследования преступления нужно провести ряд экспертиз. Причем для некоторых экспертиз необходимы результаты других. В какой последовательности следует выполнять работу для наиболее быстрого достижения результата? Для решения этой задачи применяется ориентированный граф, вершинами которого будут экспертизы, а ребра — зависимости одних от результатов других.

1. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:

   • должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности;

   • должно существовать правило, позволяющее отличать элементы друг от друга.

   Размерность множества — количество его элементов.

2. Основными операциями над множествами являются объединение, пересечение и разность.

3. В математике отношение определяет некоторую связь между двумя предметами (объектами). Любое бинарные отношение представляется множеством упорядоченных пар элементов

4. Граф — это совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Степенью вершины называется число ребер, которым принадлежит вершина. С помощью графов часто упрощается решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др.

1. http://www.mtas.ru/start/t_garf.pdf

Выполните задания к теме 17 в тетради-практикуме.