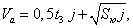Информатика и математика: Основные математические понятия и методы

16.

Основные математические понятия и методы

Успешно изучив материал, Вы будете знать:

понятия «аксиома», «теорема», «доказательство»;
основные математические структуры;
в чем суть аксиоматического метода;
принцип математического моделирования;
классификации математических моделей.

После изучения данной темы Вы будете уметь:

отличать аксиомы от теорем;
различать понятия «доказательство», «объяснение», «пример»;
формулировать задачи математического моделирования различных явлений.

После изучения материала Вы будете обладать навыками построения простейших математических моделей.

Основные понятия к теме 16

Аксиома

Теорема

Математическая структура

Моделирование

Математическая модель

Параметры математической модели

16.1.

Аксиоматический метод

Аксиоматический метод — один из способов дедуктивного построения научных теорий, при котором:

1) выбирается некоторое множество принимаемых без доказательства предложений определенной теории (аксиом ); входящие в них понятия явно не определяются в рамках данной теории;

2) все остальные предложения данной теории (теоремы ) выводятся из аксиом на основе логических рассуждений.

Первые представления об аксиоматическом методе возникли в Древней Греции (Элеаты, Платон, Аристотель, Евклид). В школьном курсе геометрии вы познакомились с системой аксиом и теорем, которые были разработаны Евклидом. Каждая следующая теорема доказывается, используя определенные правила, на основе определений, аксиом и предыдущих теорем. Если в доказательстве не допущена ошибка, нельзя получить две теоремы, утверждающие противоположное.

С другой стороны, выбрав другую систему аксиом, можно получить другую теорию, утверждающую обратное.

Например, пятая аксиома Эвклида гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной (две прямые параллельны, если они лежат в одной плоскости и нигде не пересекаются). В начале 19-го века Лобачевский предложил отменить эту аксиому и строить систему на основе 4-х аксиом Эвклида. Построенная на 4-х аксиомах геометрия Лобачевского содержит теоремы, которые противоречат эвклидовым. Новая геометрия широко применяется в картографии, космологии и пр.

Как видно на рисунке 16.1(2) Рис. 16.1. Пятая аксиома в геометрии Эвклида (1) и в геометрии Лобачевского (2) , через точку А на плоскости можно провести несколько прямых b1, b2 и т.д., параллельных данной прямой а (справа).

Различными учеными делались попытки аксиоматического изложения не только математики, но и различных разделов философии и науки (Спиноза, Ньютон и др.). При этом основное внимание уделялось определению и выбору интуитивно очевидных аксиом. Начиная со второй половины 19 в., в связи с интенсивной разработкой проблем обоснования математики и математической логики, аксиоматическую теорию стали рассматривать как формализованную систему, устанавливающую соотношения между ее элементами (знаками) и описывающую любые множества объектов, которые ей удовлетворяют. При этом основное внимание стали обращать на установление непротиворечивости системы, ее полноты, независимости системы аксиом и т.д.

В последние 30–40 лет большое внимание уделяется аксиоматизации не только математических дисциплин, но и определенных разделов физики, биологии, психологии, экономики, лингвистики, права и других наук.

Современная математика включает в себя множество разделов, описывающих разные математические объекты. Концептуальное единство математики обеспечивается как единым — аксиоматическим — методом математической деятельности, так и единым предметом ее исследования, который состоит в выделении и изучении — на основе того же аксиоматического метода — абстрактных математических структур. Математические структуры позволяют использовать однотипные рассуждения в разных разделах математики.

К таким структурам относятся, например, множества.

В математике не существует строгого определения понятия множества.

Множество — это набор элементов. Элементами множества могут быть предметы, субъекты, абстрактные понятия. Чтобы задать множество, достаточно описать, какие элементы ему принадлежат. Описанием может служить правило или простое перечисление.

Например: множество А — это множество всех студентов юридического факультета; множество В = {Иванов, Петров, Смирнов} — студенты-юристы, имеющие самый высокий рейтинг; множество R = {2<х<5, х — вещественное число}, множество T = {все законы РФ, в которых регламентируется работа СМИ} и т.д.

В теории множеств рассматриваются операции над множествами: объединение (все элементы множеств, которые объединяются), дополнение (элементы, которые не попали в множество), пересечение (элементы, которые принадлежат обоим множествам) и др. Множество может быть конечным, бесконечным, пустым (не содержать ни одного элемента).

Алгебра множеств в теории множеств — это непустая система подмножеств, замкнутая относительно дополнения и объединения, и в которой содержится пустое множество.

Множества, элементами которых являются высказывания, образуют алгебру высказываний . Используя эту структуру, можно контролировать логику доказательств (раздел математики — логика).

Если рассматривать в качестве элементов множеств события (вероятные или невозможные), то можно рассчитывать вероятность наступления того или иного случайного события (раздел математики Теория вероятности и математическая статистика).

Множество объектов можно рассматривать не по отдельности, а с учетом их связей друг с другом. Связь может быть физической (дороги, коммуникации, гены), семантической (связь слов в предложении, связь причины и следствия) или информационной (связь руководителя и подчиненных). Для описания такой структуры используют графы.

В математической теории графов и информатике граф — это совокупность объектов со связями между ними.

Объекты представляются как вершины (узлы) графа , а связи — как дуги (или ребра ).

Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или ребрах.

Например, утром автомобиль должен развезти хлеб по всем магазинам торговой сети. Узлы графа — магазины, ребра — дороги (рис. 16.2 Рис. 16.2. Пример графа ). Изучая граф, можно найти самый удобный маршрут для автомобиля. Ребра могут иметь длину (расстояние), и тогда можно найти самый короткий маршрут.

Другой пример. Граф на рис. 16.2. может описывать связи в преступной группировке. Исследуя граф, можно выяснить, кому из группировки может быть доступна та или иная информация.

16.2.

Математическое моделирование

Математика позволяет описывать различные объекты или явления с помощью математических структур, абстрагируясь от самого явления. Обычно для этого сам объект или явление заменяют более простой моделью, которая отражает только существенные свойства объекта (явления).

Модель — некоторое упрощенное подобие реального объекта, который отражает существенные особенности (свойства) изучаемого реального объекта, явления или процесса.

Один и тот же объект может описываться разными моделями, в зависимости от цели исследования

Например, моделью человека может быть манекен (для дизайнера), пластмассовый скелет (для анатома), излучатель тепловых лучей (для создания очков ночного видения) и т.д.

В качестве основания для классификации моделей берется вид языка, на котором они формулируются:

содержательная модель формулируется на естественном языке;
формальная модель воплощается с помощью одного или нескольких формальных языков (например, языков математических теорий или языков программирования).

Математические модели обычно обладают важным свойством универсальности: принципиально разные реальные явления могут описываться одной и той же математической моделью. Скажем, одно и то же уравнение описывает и поведение груза на пружине, и малые колебания маятника, колебания уровня жидкости в U-образном сосуде, изменение силы тока в колебательном контуре или колебания популяций биологических видов. Таким образом, изучая одну математическую модель, мы изучаем сразу целый класс описываемых ею явлений.

Если в естественно-научной среде математические модели обычно описаны в теории, то в гуманитарной сфере чаще используются содержательные модели, и создание математической модели оказывается сложной задачей.

По функциональному признаку модели подразделяются на описательные, объяснительные и прогностические:

описательной моделью можно назвать любое описание объекта;
объяснительные модели призваны ответить на вопрос, почему что-либо происходит;
прогностические модели должны описывать будущее поведение объекта, т.е. отвечать на вопрос, к каким изменениям приводит то или иное воздействие на исследуемый объект. Заметим, что прогностические модели совсем не обязаны включать в себя объяснительные модели. Нередко удается получить удовлетворительный прогноз на основе эмпирических обобщений, т.е. используя только данные описательной модели.

Математическое моделирование стало мощным инструментом познания окружающего мира, а математические методы исследования являются универсальным средством обоснования технических, экономических, социальных и политических решений.

В качестве математической модели могут использоваться одно или несколько уравнений, логические условия на значения переменных или параметров.

Параметр модели — величина, характеризующая конкретный объект данного класса.

Например, для расчета начальной скорости V_а по длине тормозного пути S_ю используют следующую модель:

где параметр j зависит от качества дорожного покрытия.

Существует два основных класса задач, связанных с математическими моделями: прямые и обратные. В первом случае все параметры модели считаются известными, и нам остается только исследовать ее поведение.

Например, определение начальной скорости автомобиля при известном значении j — прямая задача математического моделирования.

Порой требуется решить обратную задачу: какие-то параметры модели неизвестны (например, не могут быть измерены явно), и требуется их найти, сопоставляя поведение реальной системы с ее моделью.

Например, расчет значений j для разных типов покрытий и качества резины автомобиля — обратная задача математического моделирования.

Еще одна обратная задача: подобрать параметры модели таким образом, чтобы она удовлетворяла каким-то заданным условиям (такие задачи требуется решать при проектировании систем).

Например, расчет предельной скорости движения транспорта на данном участке дороге при известном значении j и заданном длине тормозного пути — обратная задача математического моделирования.

Чем сложнее система — чем больше в ней существенных связей между объектами, тем больше уравнений и параметров будет содержать математическая модель.

Основные выводы

Аксиоматический метод — один из способов дедуктивного построения научных теорий, при котором:
Множество — это набор элементов. Элементами множества могут быть предметы, субъекты, абстрактные понятия. Чтобы задать множество, достаточно описать, какие элементы ему принадлежат. Описанием может служить правило или простое перечисление.
В математической теории графов и информатике граф — это совокупность объектов со связями между ними. Объекты представляются как вершины (или узлы) графа, а связи — как дуги (или ребра).
Модель — некоторое упрощенное подобие реального объекта, который отражает существенные особенности (свойства) изучаемого реального объекта, явления или процесса. Параметр модели — величина, характеризующая конкретный объект данного класса

Контрольные вопросы

Что такое «аксиома», «теорема», «определение»?
Могут ли две теории, базирующиеся на одних и тех же аксиомах, противоречить друг другу?
Могут ли существовать разные системы аксиом, описывающие один и тот же объект?
Какие математические структуры вы знаете?
В чем преимущество использования структур?
Почему математика является универсальным языком моделирования?
Почему моделирование является основой познания окружающего мира?
Опишите различные подходы к классификации математических моделей.

Интернет-источники

Задания для самостоятельной работы

Выполните задания к теме 16 в тетради-практикуме.