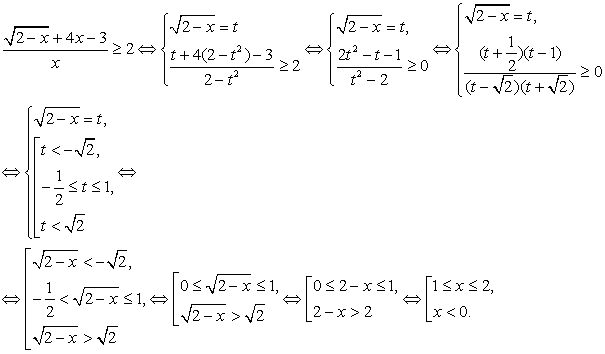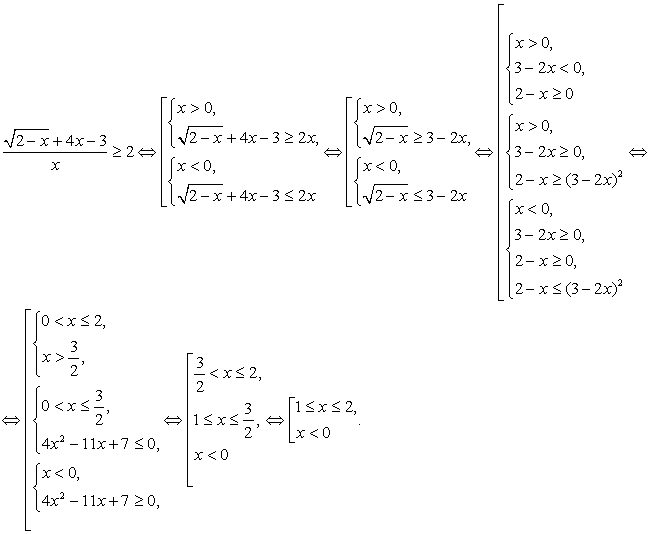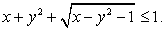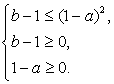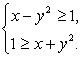Комментарий. Сущность процесса решения уравнений можно описать следующим образом: исходное уравнение упрощается посредством определенных преобразований, т.е. выстраивается цепочка от исходного к некоторому итоговому уравнению, решение которого очевидно или способ (алгоритм) решения которого хорошо известен. При этом возможны три типа преобразований, три принципиально разные ситуации.
-
Применяемые в процессе решения преобразования таковы, что множества корней исходного и итогового уравнений совпадают; в этом случае исходное и итоговое уравнения называют равносильными; соответствующие преобразования также называют равносильными.
-
Применяемые в процессе решения преобразования таковы, что множество корней итогового уравнения «шире», чем множество корней исходного уравнения; в этом случае говорит, что в процессе решения применены неравносильные преобразования, которые могли привести к появлению посторонних корней.
-
Применяемые в процессе решения преобразования таковы, что множество корней итогового уравнения «уже», чем множество корней исходного уравнения; в этом случае говорят, что в процессе решения применены неравносильные преобразования, которые могли привести к потере корней.
Проиллюстрируем сказанное примерами.
Пример 6.1.
Перепишем уравнение, разложив на множители знаменатели:
Умножим обе части уравнения на выражение x2
+ 4; это равносильное преобразование, т.к. x2
+ 4 ≠ 0 при любом значении х: 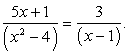
Возведем обе его части в квадрат:
Так как 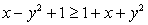 , то получаем
, то получаем 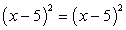 . Множество корней этого уравнения — все действительные числа. При этом простая проверка показывает, что отрицательное число не может быть корнем исходного уравнения. Таким образом, в процессе решения были применены неравносильные преобразования и появились посторонние корни. Действительно, возведение обоих частей уравнения в четную степень является равносильным преобразованием только в том случае, если обе части уравнения неотрицательны.
. Множество корней этого уравнения — все действительные числа. При этом простая проверка показывает, что отрицательное число не может быть корнем исходного уравнения. Таким образом, в процессе решения были применены неравносильные преобразования и появились посторонние корни. Действительно, возведение обоих частей уравнения в четную степень является равносильным преобразованием только в том случае, если обе части уравнения неотрицательны.
в) Дано уравнение: x2 - 2х – 3 = 4х + 5 + x2 .
Перепишем уравнение, разложив квадратные трехчлены на множители:
(х + 1)(х - 3) = (5 - х)(х + 1).
Разделим обе части уравнения на выражение х + 1 : х – 3 = 5 - х.
Последнее уравнение имеет единственный корень х = 4, в то время как исходное уравнение имеет два корня: x1 = 4 и x2 = -1. Таким образом, в процессе решения уравнения было применено неравносильное преобразование, которое привело к потере корней. Действительно, проводя деление на выражение х + 1, мы не потребовали, чтобы х + 1 ≠ 0.
Как видно из примеров неравносильные преобразования могут стать причиной неверного решения уравнения, привести к ошибке. Так может быть запретить неравносильные преобразования?! Можно запретить. Это один из возможных подходов. Он снимает проблему посторонних и потерянных корней, но приводит, как правило, к некоторому техническому усложнению процесса решения уравнения: появляются смешанные системы (уравнение и неравенство) и совокупности таких систем.
Так, уравнение 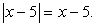 из примера 6.1, б равносильно совокупности:
из примера 6.1, б равносильно совокупности:
Уравнение x2
- 2х – 3 = 4х + 5 - x2
из примера 6.1, в равносильно совокупности 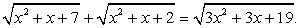
Рассмотренные совокупности решаются просто, но в более сложных случаях обязательное соблюдение условия равносильности преобразований может привести к серьезным техническим трудностям, сделать решение слишком ветвящимся и громоздким. Поэтому, не будем строго запрещать применение любых неравносильных преобразований. Все ли они одинаково опасны? Понятно, что более опасны неравносильные преобразования, приводящие к потере корней. В примере 6.1, в нам удалось легко понять причину потери корня и исправиться, но в большинстве случаев потерянные корни отыскать весьма трудно (заметим также, что малоопытный решающий, а абитуриент часто именно таков, может вовсе не заметить факта потери корня, и не будет пытаться его отыскать, хотя это, может быть, и получилось бы).
Итак, на не равносильные преобразования, приводящие к потере корней, мы накладываем строгий и категорический запрет. При решении уравнений, таким образом, мы не будем применять деление обеих частей уравнения на выражение, обращающееся в ноль в области определения уравнения, и не будем применять преобразования, приводящие к сужению области определения уравнения.
Что же касается, неравносильных преобразований, приводящих к появлению посторонних корней, то такие преобразования вполне допустимы. Но при этом, обязательным заключительным этапом решения должна быть проверка всех найденных в итоге корней. Заметим, что тактика проверки зависит непосредственно от класса уравнений (рациональные, иррациональные, логарифмические и т.д.), ибо в каждом случае свои причины появления посторонних корней. В этой связи, тактика проверки конечно должна быть гибкой, но можно пользоваться и универсальным приемом: подстановка всех корней итогового уравнения в исходное с последующим вычислением или «прикидкой».
Пример 6.2.
Комментарий. При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования при обязательной проверке корней. Решая уравнения вида, 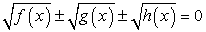 следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.
следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.
Решение
В нашем уравнение сумма коэффициентов при х в первом и третьем подкоренных выражениях равна коэффициенту при х во втором подкоренном выражении. Поэтому уединить целесообразно именно корень 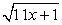 . Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.
. Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.
Итак, имеем:
Комментарий. При решении иррационального уравнения мы осуществляем так называемую рационализацию уравнения, т.е. избавляемся от радикалов (корней). Но, избавляясь от корней, мы избавляемся и от ограничений на подкоренные выражения: 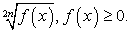 Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой:
Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой:
Решив эту систему, получаем область определения уравнения:
Очевидно, что 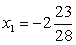 — посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x2
= 0 —– принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).
— посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x2
= 0 —– принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).
Ответ:  х = 0.
х = 0.
Комментарий. Но единственная ли причина появления посторонних корней при решении иррациональных уравнений с радикалами четной степени — расширение области определения исходного уравнения? Не кроется ли в возведении обеих частей уравнения в четную степень еще одна, менее очевидная, но не менее опасная в смысле ошибки, причина появления посторонних корней?
Пример 6.3.
При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования, т.е. возведем обе части уравнения в квадрат, решим полученное рациональное уравнение и сделаем проверку корней.
Проверим, удовлетворяют ли эти корни исходному уравнению.
Пусть х = -1, тогда левая часть исходного уравнения равна -6. Таким образом, х = -1 — посторонний для исходного уравнения корень, появившийся в процессе решения из-за применения неравносильных преобразований. Пусть теперь, х = 7. Тогда исходное уравнение превращается в верное числовое равенство. Исходное уравнение, таким образом, имеет единственный корень х = 7.
б) Решим теперь уравнение 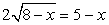 (его чрезвычайно, малое отличие от предыдущего уравнения очевидно).
(его чрезвычайно, малое отличие от предыдущего уравнения очевидно).
Поступая так же, как в случае «а», получаем:
Итоговое уравнение имеет такие же корни, что и уравнение из случая «а». Проверим их подстановкой в исходное уравнение 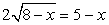 . Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.
. Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.
В процессе решения следствием уравнений «а», «б» является одно и тоже уравнение 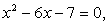 имеющее два корня: x1
= -1 и x2
= 7. Корень x1
= -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x2
= 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».
имеющее два корня: x1
= -1 и x2
= 7. Корень x1
= -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x2
= 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».
В каждом из случаев «а» и «б» корни, оказавшиеся посторонними, принадлежат области определения данного уравнения. Значит, расширение области определения исходного уравнения — не единственная причина появления посторонних корней. В чем же дело? Заметим, что и в случае «а», и в случае «б» при подстановке в исходное уравнение корень, оказывающийся посторонним, приводит к ситуации: левая и правая части уравнения равны по абсолютной величине, но противоположны по знаку. Это не случайно. Уравнение 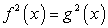 является следствием не только уравнения
является следствием не только уравнения 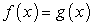 , но и следствием уравнения
, но и следствием уравнения 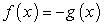 . Какие следует сделать из этого выводы?
. Какие следует сделать из этого выводы?
Во-первых, поскольку появление посторонних корней при решении иррациональных уравнений, содержащих радикалы четной степени может быть и не связано с областью определения исходного уравнения, то и проверка корней не может осуществляться только по области определения, или условиям ее задающим.
Во-вторых, проверка корней иррационального уравнения, должна учитывать обе причины появления посторонних корней; универсальный прием, как уже говорилось, состоит в непосредственной подстановке в исходное уравнение, но могут быть реализованы и другие подходы.
-
Сначала отсечь те корни, которые не принадлежат области определения исходного уравнения, а оставшиеся проверить непосредственной подстановкой во все уравнения левая и правая части которых возводились в квадрат в процессе решения.
-
Опять же исключить все корни, не принадлежащие области определения, а затем проанализировать все случаи возведения в квадрат обеих частей уравнения, выделить те случаи, где было нарушено условие равносильности:
Далее только в эти уравнения подставить корни итогового уравнения, принадлежащие области определения исходного уравнения.
-
Если решать иррациональные уравнения, применяя только равносильные преобразования, то в каждом случае возведения в квадрат следует предусматривать условие равносильности, сформулированное выше, и изначально следует зафиксировать условия, задающие область определения исходного уравнения.
Рассмотрим схемы равносильных преобразований для иррациональных уравнений основных видов.
Заметим, что важно, конечно, не выучить наизусть эти схемы, а понять их, уметь самостоятельно составлять схемы равносильности для других случаев.
Не надо думать, что в процессе решения иррационального уравнения обязательно появляются посторонние корни. Рассмотрим пример.
Пример 6.4.
Решение
Возведя обе части уравнения в квадрат, получаем 1 + 3х = x2 + 2х + 1, т.е. уравнение x2 – х = 0. Его корни x1 = 0 и x2 = 1. Подставляя каждый из найденных корней в исходное уравнение, убеждаемся, что оба они являются его корнями.
Пример 6.5.
Решение
Возведем обе части уравнения в квадрат (дважды):
Корни последнего уравнения:
Далее следует провести проверку корней. Область определения исходного уравнения задается условиями 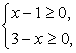 т.е. 1 ≤ x ≤ 3. Как нетрудно проверить, полагая
т.е. 1 ≤ x ≤ 3. Как нетрудно проверить, полагая 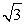 приближенно равным 1,7, что оба корня x1
и x2
принадлежат области определения исходного уравнения. Значит, если среди x1
и x2
есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения
приближенно равным 1,7, что оба корня x1
и x2
принадлежат области определения исходного уравнения. Значит, если среди x1
и x2
есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения 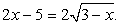 Непосредственной подстановкой именно в это уравнение проверим наши корни x1
и x2
.
Непосредственной подстановкой именно в это уравнение проверим наши корни x1
и x2
.
Мы пришли к верному числовому равенству. Значит 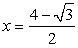 — корень данного уравнения.
— корень данного уравнения.
Ясно, что левая часть уравнения отрицательна, а правая положительна. Поэтому 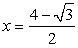 — посторонний корень.
— посторонний корень.
Пример 6.6.
Распределим радикалы следующим образом: 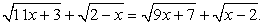
Возведем обе части уравнения в квадрат и приведем подобные слагаемые:
Возведем обе части полученного уравнения в квадрат, раскроем скобки и приведем подобные слагаемые:
Проведем проверку корней. Сразу замечаем, что корень 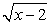 не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.
не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.
Пример 6.7.
При решении этого уравнения покажем применение метода введения новой переменной при решении иррациональных уравнений.
Возведем обе части уравнения в квадрат: 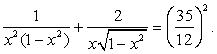
Пусть теперь 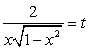 , тогда уравнение можно переписать в виде:
, тогда уравнение можно переписать в виде:
Это уравнение имеет два корня: 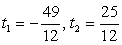 . Таким образом, следствием исходного уравнения является совокупность систем:
. Таким образом, следствием исходного уравнения является совокупность систем:
Решим первую систему совокупности.
Корни этой совокупности систем: 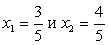
Аналогично, решая вторую систему исходной совокупности, получаем:
Пример 6.8.
Подкоренные выражения 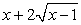 и
и 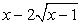 представляют из себя полные квадраты:
представляют из себя полные квадраты:
Тогда:
Пусть 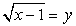 , тогда уравнение можно переписать в виде:
, тогда уравнение можно переписать в виде:
Возведем обе части последнего уравнения в квадрат, затем воспользуемся тождеством 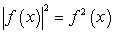 и формулой разности квадратов:
и формулой разности квадратов:
Если у = 0, то 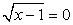 , т.е. х = 1. Если у = 2, то
, т.е. х = 1. Если у = 2, то 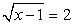 , т.е. х = 5. Если у = 1, то
, т.е. х = 5. Если у = 1, то 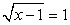 , т.е. х = 2. Если у = -1, то уравнение
, т.е. х = 2. Если у = -1, то уравнение 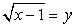 не имеет корней.
не имеет корней.
Непосредственной подстановкой в исходное уравнение всех найденных значений х, приходим к выводу, что только х = 5 является корнем данного уравнения.
Рассмотрим далее примеры решения иррациональных уравнений с корнями степени, большей, чем вторая.
Пример 6.9.
Возведем обе части уравнения в третью степень:
Выражение в скобках, очевидно, есть — 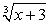 , т.е.:
, т.е.:
Снова возведем обе части уравнения в третью степень:
Далее имеем:
В процессе решения, был применен прием, связан ный с заменой суммы 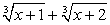 на выражение
на выражение 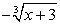 , что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.
, что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.
Если х = -2, то исходное уравнение обращается в верное числовое равенство.
Для подстановки значений 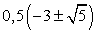 возьмем приближенное значение:
возьмем приближенное значение: 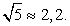 Тогда
Тогда 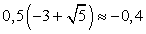 и
и 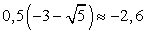 .
.
Если х = -0,4, то:
Ясно, что это числовое равенство неверно, поскольку все три значения корней положительны, а сумма положительных чисел не может быть равна 0.
Если х = -2,6, то:
Ясно, что эта сумма не может быть равна 0, т.к. уже 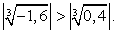 Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).
Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).
Таким образом, х = -2 — единственный корень данного уравнения.
Ответ:  -2.
-2.
Комментарий. Запишем в общем виде прием решения, рассмотренный в этом примере:
По аналогичной схеме решаются уравнения вида 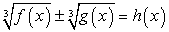 .
.
Большие трудности у абитуриентов вызывают иррациональные уравнения, содержащие радикалы разных степеней. Рассмотрим примеры.
Пример 6.10.
Это уравнение легко рационализируется возведением обеих его частей в шестую степень:
И далее:
Подстановкой выясняем, что только х = 2 является корнем данного уравнения.
В этом случае возведение обеих частей уравнения в шестую степень уже нецелесообразно. Проведем замену переменных.
Пусть 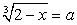 и
и 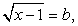 тогда a + b = 1. Возведем в куб первое уравнение системы
тогда a + b = 1. Возведем в куб первое уравнение системы 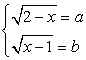 ,и в квадрат второе уравнение этой системы; затем почлено сложим полученные уравнения. В итоге получаем: a3
+ b2
= 1.
,и в квадрат второе уравнение этой системы; затем почлено сложим полученные уравнения. В итоге получаем: a3
+ b2
= 1.
Таким образом, имеем систему уравнений:
Решая ее, получаем: 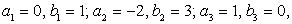 т.е. совокупность систем:
т.е. совокупность систем:
В итоге 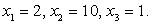 Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.
Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.
Комментарий. Заметим, что описанный в случае «б» прием является достаточно распространенным. Рассмотрим его применение при решении уравнений с радикалами высших степеней.
Пример 6.11.
Пусть 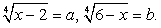 Тогда
Тогда 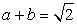 . Возведем в четвертую степень обе части каждого из уравнений системы
. Возведем в четвертую степень обе части каждого из уравнений системы 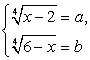 , и почленно сложим полученные уравнения. В итоге получаем:
, и почленно сложим полученные уравнения. В итоге получаем: 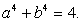
Таким образом, имеем систему уравнений: 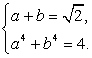
Это симметрическая система уравнений, стандартно решающаяся заменой переменных a + b = y и ab = z.
Имеем корни: 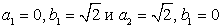 . Отсюда x1
= 2, x2
= 6. Проверка показывает, что это действительно корни данного уравнения.
. Отсюда x1
= 2, x2
= 6. Проверка показывает, что это действительно корни данного уравнения.
Ответ:  x1
= 2, x2
= 6.
x1
= 2, x2
= 6.
Пример 6.12.
Аналогично предыдущему примеру получаем симметрическую систему относительно переменных 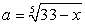 и
и 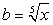 :
:
Корни этой системы легко угадываются: 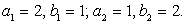 Далее получаем корни исходного уравнения: x1
= 1 и x2
= 32.
Далее получаем корни исходного уравнения: x1
= 1 и x2
= 32.
Ответ:  x1
= 1, x2
= 32.
x1
= 1, x2
= 32.
Комментарий. Рассмотрим далее несколько примеров решения иррациональных неравенств. Все они, как мы уже обсуждали, решаются применением исключительно равносильных преобразований. Поэтому приведем схемы основных равносильных переходов ( ).
).
Комментарий. Представленные схемы принципиально не изменяются, если исходно рассматривать нестрогие неравенства.
Пример 6.13.
Решение
Применим схему V:
Таким образом, решение неравенства: 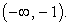
Пример 6.14.
Решение
Применим схему III:
Таким образом, решение неравенства: 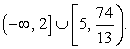
Пример 6.15.
Решение
Перераспределим радикалы: 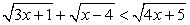 и, воспользовавшись в качестве принципиального ориентира схемой I, получаем:
и, воспользовавшись в качестве принципиального ориентира схемой I, получаем:
Таким образом, решение неравенства: [4, 5).
Ответ:  [4, 5).
[4, 5).
Пример 6.16.
Решение
Преобразуем первую дробь, и будем решать неравенство, применяя метод введения новой переменной:
Таким образом, решение неравенства: (2, 8).
Ответ:  (2, 8).
(2, 8).
Пример 6.17.
На этом примере мы также как и в предыдущем случае посмотрим особенности применения метода введения новой переменной при решении иррациональных неравенств.
Комментарий. Можно было решить это неравенство и без применения метода введения новой переменной, рассмотрев отдельно (в совокупности) случаи, задаваемые условиями х > 0 и x < 0. Приводим запись такого решения:
Результат, естественно не зависит от способа решения: 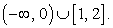
В заключение рассмотрим пример решения иррационального неравенства с двумя переменными (группа С).
Пример 6.18.
Решение
Пусть 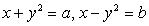 , тогда неравенство можно записать в виде:
, тогда неравенство можно записать в виде: 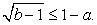
По известной нам схеме это неравенство равносильно системе:
Итак, условия 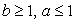 должны выполняться одновременно, т.е. должна выполняться система:
должны выполняться одновременно, т.е. должна выполняться система:
Из нее следует, что 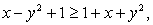 т.е.
т.е. 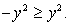 Это означает, что y = 0.
Это означает, что y = 0.
Подставим найденное значение в исходное неравенство; получим неравенство,  из которого следует, что x = 1.
из которого следует, что x = 1.
Таким образом, решение данного неравенства: x = 1, y = 0.
Ответ:  x = 1, y = 0
x = 1, y = 0
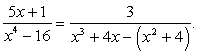
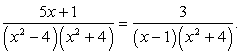
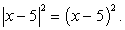
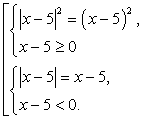
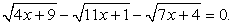
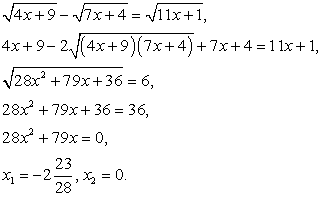
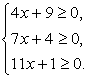
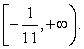
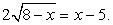
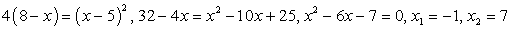
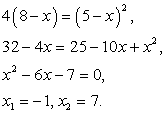
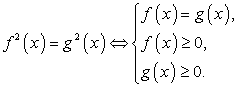
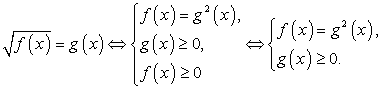
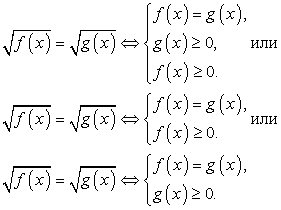
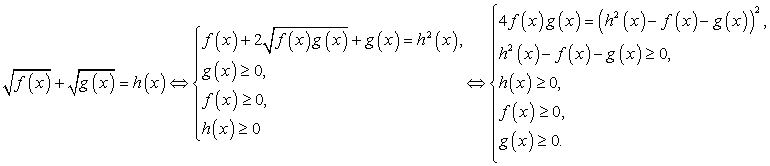
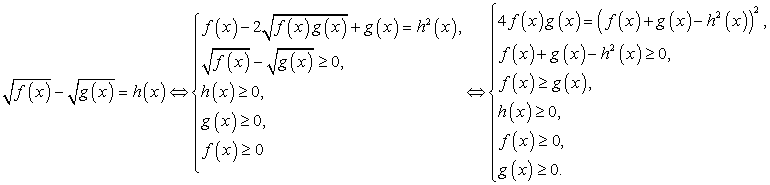
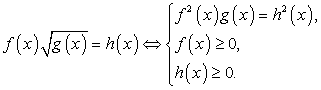
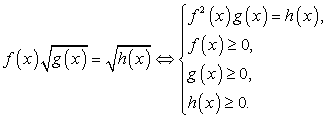
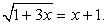
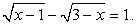
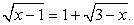
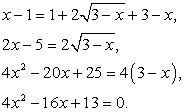
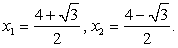
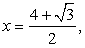 тогда:
тогда: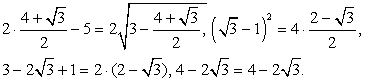
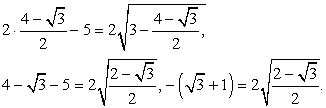
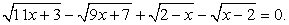
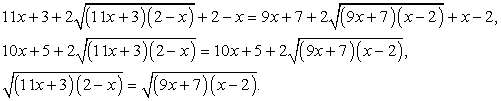
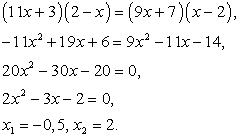
 .
. .
. .
. и
и 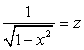 .
.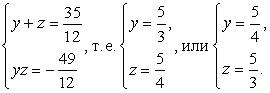
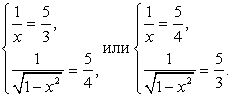
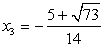 .
.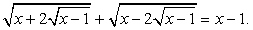
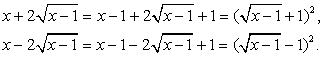
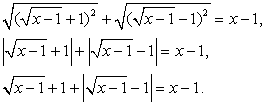
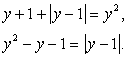
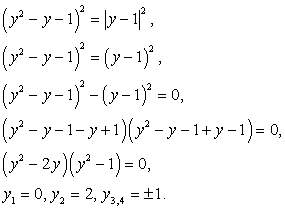
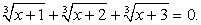
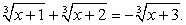
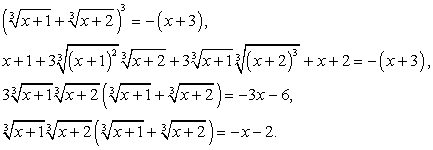
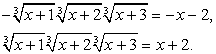
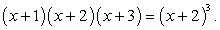
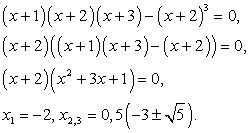
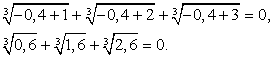
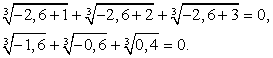
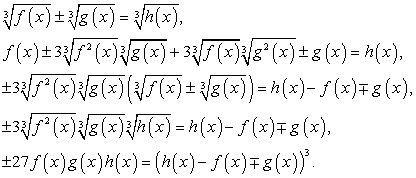
 .
.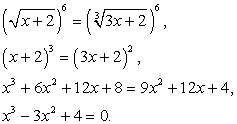
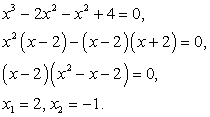
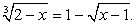
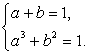
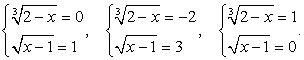
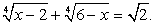
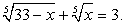
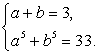
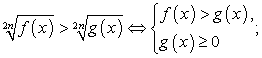
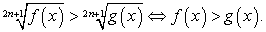
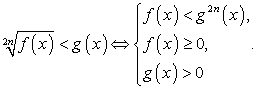
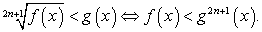
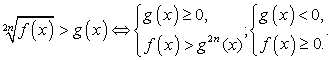
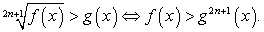
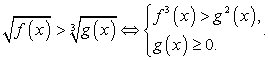
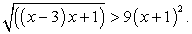
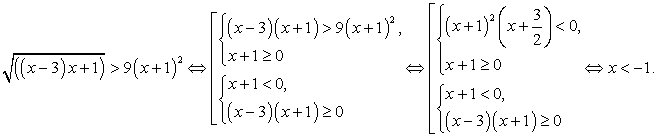
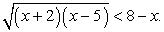
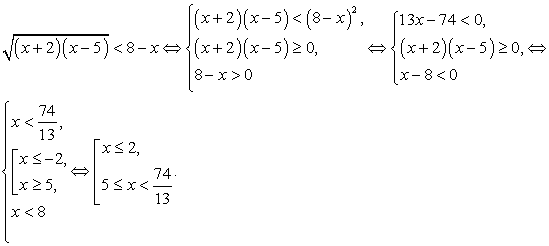
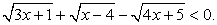
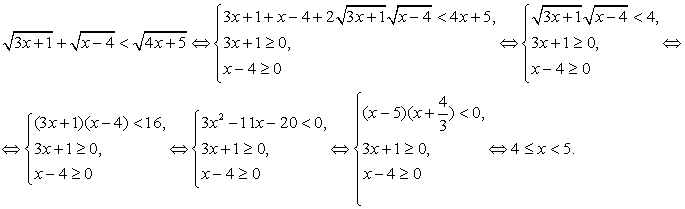
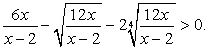
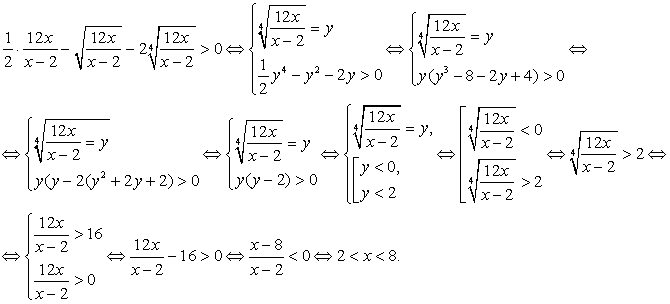
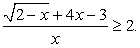
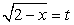 , тогда
, тогда 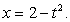 Таким образом:
Таким образом: