§ 4.2.3. Принцип оптимальности Беллмана. Уравнения Беллмана

 

Предположим, что задача

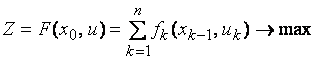
имеет решение.

Тогда справедлив принцип оптимальности Беллмана: оптимальное управление  обладает тем свойством, что каковы бы ни были состояния системы  на любом шаге и управление , принимаемое в этом состоянии, последующие управляющие решения , ...,  должны составлять оптимальную стратегию относительно состояния , полученного в результате управляющего решения , т.е. состояния, к которому придет система в конце данного шага.

Другими словами: управление на каждом шаге необходимо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге.

На основании принципа оптимальности Беллмана можно получить основное уравнение динамического программирования, или уравнение Беллмана.

Рассмотрим последовательность задач используя принцип оптимальности. На каждом шаге любого состояния системы  управление  нужно выбирать “с оглядкой”, т.к. этот выбор влияет на последующее состояние  и дальнейший процесс управления, зависящий от . Это следует из принципа оптимальности.

Как отмечалось ранее, среди всех шагов есть одно исключение, он может планироваться попросту, без оглядки на будущее – это последний шаг. Этот шаг единственный, который можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.

Рассмотрим ый шаг: – состояние системы к началу го шага,   – конечное состояние,  – управление на шаге , а  - целевая  функция шага .

Согласно принципу оптимальности,  нужно выбирать так, чтобы для любых состояний  получить максимум целевой функции на этом шаге.

Обозначим через  максимум показателя эффективности шага  при условии, что к началу последнего шага система была в произвольном состоянии , а на последнем шаге управление было оптимальным.

                                               (5)

Управление , при котором достигается максимум (5) также зависит от  и называется условным оптимальным управлением шага  и обозначается .

Решив задачу (5), найдем для всех возможных состояний  две функции:  и .

Рассмотрим двухшаговую задачу: присоединим к му шагу -ый (рисунок 19).

                                            

 

                         

 

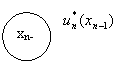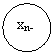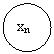Рис. 19. Оптимальное управление на двух последних шагах

 

Для любых состояний , произвольных управлений  и оптимального управления на шаге  значение целевой функции на двух последних шагах равно:

                                                (6)

Согласно принципу оптимальности для любых состояний  управление нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем шаге приводило бы к максимальному эффекту на двух последних шагах. Следовательно, необходимо искать максимум (6) по всем допустимым .

              (7)

В результате максимизации получаем две функции:  и .

Далее рассматривается трехшаговая задача: к двум последним добавляется -ой и т.д.

Обозначим через  условный максимум целевой функции, полученный при оптимальном управлении на  шагах, начиная с го до конца, при условии, что к началу го шага система находится в состоянии .

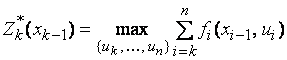
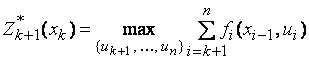
Целевая функция на  последних шагах при произвольном управлении  на ом шаге и оптимальном управлении на последующих  шагах равна .

Согласно принципу оптимальности,  выбирается из условия максимума этой суммы, т.е.

    (8)

Уравнения (8) называются уравнениями Беллмана. Это рекуррентные соотношения, позволяющие найти предыдущие значения функции, зная последующие. Процесс решения уравнений (5) и (8) называется условной оптимизацией.

В результате условной оптимизации получаем две последовательности:  и .

Используя эти последовательности, можно найти решение задачи динамического программирования при данных  и :  .

 

 

К оглавлению

Назад к разделу "§ 4.2.2. Принцип решения задач динамического программирования"

Вперед к разделу "§ 4.3. Элементы теории управления запасами"