ГЛАВА 3. АЛГЕБРА МАТРИЦ (ПРОДОЛЖЕНИЕ)

 

3.1. Обратная матрица

 

Пусть задана квадратная матрица  порядка n.

Определение. Квадратная матрица А^-1 порядка n называется обратной к матрице А, если она удовлетворяет соотношению

 

(3.1.1)

Присоединенной матрицей квадратной матрицы А называется матрица А*, каждый элемент  которой есть алгебраическое дополнение элемента  транспонированной матрицы А, т.е.

.

 

Квадратная матрица А называется невырожденной (неособенной), если ее определитель |A| отличен от нуля, и вырожденной, если |A|=0.

 

Теорема. Для всякой невырожденной матрицы А существует единственная обратная матрица А^-1, определяемая следующим выражением:

(3.1.2)

Доказательство. Докажем сначала единственность. Предположим, что существуют две различные обратные матрицы  и . Тогда имеем

 

	(3.1.3)
	(3.1.4)

 

Из двух последних равенств следует, что =.

Покажем теперь, что выражение (3.1.2) действительно задает обратную матрицу. Составим произведение АА^*. Очевидно, что элементами данного произведения являются суммы произведений элементов строк матрицы А на алгебраические дополнения, т.е. . Как известно из гл.2, при i=j=0. В итоге получаем

,

 

или ,

откуда .

В заключение отметим, что А^* перестановочна с А, т.е. , что видно непосредственно. Теорема доказана.

Пример. Вычислить обратную матрицу для матрицы А, равной:

                                      .

Решение. . Вычислим присоединенную матрицу А^*:

А₁₁=-3, А₁₂=-1, А₂₁=-1, А₂₂=2,

; .

 

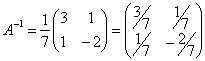Проверкой убеждаемся, что АА^-1=Е.

 

Обратная матрица обладает следующими свойствами:

1.     Определитель обратной матрицы равен обратной величине определителя исходной матрицы, т.е. |A^-1|=.

2.     Произведение двух невырожденных матриц А и В является невырожденной матрицей и .

3.     Если матрица А невырожденная, то .

4.     Обратная матрица к транспонированной является транспонированной матрицей к обратной, т.е. .

 

 

К оглавлению

Назад к разделу "2.5. Задания для самостоятельной работы по главе 2"

Вперед к разделу "3.2. Ранг матрицы"