1.10. Линейная зависимость и независимость векторов
Система векторов 
называется
линейно-зависимой, если хотя бы один из этих векторов является линейной
комбинацией остальных, т.е. некоторый вектор 
можно представить в
виде:
,
где 
- числовые множители.
В противоположном случае система векторов называется
линейно-независимой. Существует и другое определение линейной зависимости
системы векторов. Система векторов называется
линейно-зависимой, если существует такие числа 
, по крайней мере, одно из которых отлично от нуля, что имеет
место равенство:
.
Если же это равенство имеет место тогда и только
тогда, когда 
, то система векторов линейно-независима.
В n-мерном пространстве существует не более n линейно-независимых векторов. Любая система векторов, состоящая из числа векторов, больше n, является линейно-зависимой в этом пространстве.
Пример 1.
Определить, является ли система векторов 
=(3,0,1); 
=(4,1,-2); 
=(1,4,3); 
=(0,2,-1) линейно-зависимой. Если является, то один из
векторов выразить как линейную комбинацию других.
Решение. Имеем четыре вектора в трехмерном пространстве. Следовательно, данная система векторов является линейно-зависимой. Можно решить эту задачу, воспользовавшись вторым определением линейной зависимости системы векторов. Запишем уравнение:
.
Определим значения 
, для этого в равенство подставим данные вектора и произведем
соответствующие действия:
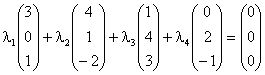
Умножим каждый вектор на 
и сложим полученные
векторы.
Учитывая, что два вектора равны в том случае, если равны их соответствующие координаты, получим однородную систему линейных уравнений:
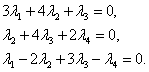
Решаем данную систему методом Жордана-Гаусса:
На первом шаге принимаем «1» в третьей строке за направляющий элемент, меняем местами данную строку с первой и получаем нули в первом столбце. На втором шаге принимаем за направляющий элемент «1», стоящий во второй строке и во втором столбце. С помощью этой строки получаем нули во втором столбце. На третьем шаге принимаем «-48» за направляющий элемент и делим третью строку на «-48». С помощью полученной строки получаем нули в третьем столбце. Последняя матрица соответствует системе уравнений:
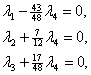
откуда получаем:
Найденные значения 
подставим в исходное
равенство:
Полагая 
, разделим полученное равенство на 
. В результате будем иметь следующую зависимость между
векторами:
Заметим, что из полученного равенства любой из векторов можно представить, как линейную комбинацию остальных векторов, например:
Упражнения.
1.10.1. Найти линейную комбинацию 
векторов 
=(4,1,4,-
2), 
=(1,2,-3,2), 
=(16,9,1,-3).
1.10,2. Найти вектор 
из уравнения:
, если 
=(5,-8,- 1,2), =(2,- 1,4,-3) и 
=(-3, 2, -5, 4).
Выяснить, являются ли следующие системы векторов линейно-зависимыми или линейно-независимыми. Если система векторов линейно-зависима, то установить эту зависимость:
1.10.3. =(3, 5, 0, 4) и = (0, 1, 2, - 3).
1.10.4. = (1, 2, 4), =(3,
5, 1) и =(0, 1, -1).
1.10.5. =(2, 1, 3), =(5, 3, 2) и 
=(1, 4, 3),
1.10.6. = (3, 4, -5), =(8, 7, -2) и =(1, 4, 3), =(2, -1, 8).
1.10.7. =(2, -5, 1, 2), =(-3, 7, -1, 4), =(5, -9, 2, 7) и =(4,-6, 1, 2).
1.10.8. =(4, -5, 2, 6), =(2, -2, 1, 3), =(6,
-3, 3, 9) и =(2,-1, 1, 3).
1.10.9. Найти все значения Q, при
которых вектор 
=(7,-2,Q) линейно выражается
через векторы: =(2, 3, 5), =(3,
7, 8) и =(1,
-6, 1).
1.10.10. Найти
все значения Q,
при которых вектор =(5, 9, Q) линейно выражается через векторы: =(4,
4, 3), =(7, 2, 1) и =(4, 1, 6).
Установить линейную зависимость следующей системы векторов и выразить один из векторов системы в виде линейной комбинации остальных:
1.10.11. =(5, -3, 2, 4), =(2, -1, 3, 5) и =(-4, -3, -5, -7).
1.10.12. =(8, 7, 4, 5), 
=(3, 2, 1, 4) и =(0, 5, 4, -17).
1.10.13. =(3, 2, 1), =(0,1,2), =(1,-1,-2) и =(9, 2,
-2).
1.10.14. =(3, 1,4), =(-1,2,0), =(2,1,-7) и 
=(11, -3, 1).
1.10.15. =(4, -5,2,6), =(2,-2,1,3), =(2, - 2,1,3) и 
=(4, -1,5,6).
1.10.16. =(1,2, 1, 1), =(1,1,1,1), =(1,1,-1,-1), =(1, -1, 1, -1) и 
=(1, -1, -1, 1).
Назад к разделу "1.9. Действия над векторами"
Вперед к разделу "1.11. Базис системы векторов. Переход от одного базиса к другому"