1.8. Однородные системы линейных уравнений
Однородной называется система линейных уравнений, свободные члены которой равны нулю.
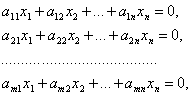 (1)
(1)
Очевидно, что система однородных уравнений (1) всегда
совместна, так как имеет нулевое решение ![]() . Это следует также из теоремы Кронекера - Капелли: в случае
однородной системы
. Это следует также из теоремы Кронекера - Капелли: в случае
однородной системы ![]() .
.
При решении системы однородных уравнений можно поставить вопрос: при каком условии однородная система (1) является неопределенной, т.е. имеет ненулевые решения. Ответ на этот вопрос дает следующая теорема.
Теорема. Для того чтобы система (1) имела ненулевые решения необходимо и достаточно, чтобы выполнялось условие r(A)<n.
Действительно, если r(A)=n, то система имеет единственное и, значит, только
нулевое решение: ![]() .
.
Еслиr(A)<n, то система (1) является неопределенной (несовместной она быть не может) и, значит, имеет бесчисленное множество решений.
Пусть ![]() - какое-нибудь
ненулевое решение однородной системы (1). Представим это решение как
вектор-строку
- какое-нибудь
ненулевое решение однородной системы (1). Представим это решение как
вектор-строку ![]() . Тогда
. Тогда ![]() тоже, очевидно, будет
решением системы (1). Далее, если
тоже, очевидно, будет
решением системы (1). Далее, если ![]() какое-то другое
решение системы (1), отличное от
какое-то другое
решение системы (1), отличное от ![]() , то при любых
, то при любых ![]() и
и ![]() линейная комбинация
линейная комбинация
![]() данных решений тоже будет решением системы, так как если
данных решений тоже будет решением системы, так как если
![]()
то и ![]() .
.
Итак, любая линейная комбинация решений однородной системы (1) тоже будет ее решением.
Определение.
Линейно независимая система решений ![]() системы (1) называется
фундаментальной, если каждое решение системы (1) является линейной комбинацией
решений
системы (1) называется
фундаментальной, если каждое решение системы (1) является линейной комбинацией
решений ![]() .
.
Теорема. Если r(A)<n, то система (1) обладает фундаментальными системами решений. Рассмотрим систему уравнений
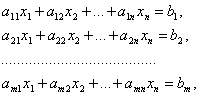
![]() (2)
(2)
и соответствующую ей систему однородных уравнений
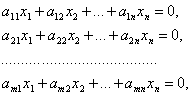 (3)
(3)
Пусть ![]() - какое-то решение
системы (2) и
- какое-то решение
системы (2) и ![]() любое другое ее
решение, отличное от
любое другое ее
решение, отличное от![]() . Очевидно, что разность
. Очевидно, что разность ![]() будет решением системы
(3), и если
будет решением системы
(3), и если ![]() - произвольное решение
однородной системы (3), то очевидно, что
- произвольное решение
однородной системы (3), то очевидно, что ![]() является решением системы
(2). Отсюда следует, что все решения системы (2) можно получить, прибавляя к
одному какому-нибудь ее решению всевозможные решения однородной системы (3).
является решением системы
(2). Отсюда следует, что все решения системы (2) можно получить, прибавляя к
одному какому-нибудь ее решению всевозможные решения однородной системы (3).
Таким образом, общее решение системы (2) равно
линейной комбинации общего решения однородной системы (3) и произвольного, но
фиксированного решения системы (2). Если ![]() фундаментальная
система решений однородной системы (3) и
фундаментальная
система решений однородной системы (3) и ![]() - произвольное фиксированное
решение системы (2), то общее решение системы (2) имеет вид
- произвольное фиксированное
решение системы (2), то общее решение системы (2) имеет вид ![]() , где
, где ![]() - произвольные числа.
- произвольные числа.
Пример. Найти фундаментальную систему однородной системы уравнений.
![]()
Решение. Решаем систему методом Жордана-Гаусса:
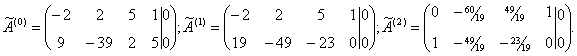
Общее решение имеет вид:
![]()
Решение ![]() получим, придавая
свободным неизвестным значения
получим, придавая
свободным неизвестным значения ![]() :
:
![]() , и решение
, и решение ![]() получим, полагая
получим, полагая ![]() :
:
![]() . Таким образом, одна
из фундаментальных систем решений имеет вид:
. Таким образом, одна
из фундаментальных систем решений имеет вид:
![]() ,
,![]() .
.
Общее решение системы можно представить в следующем
виде: ![]() где
где ![]() - произвольные числа.
- произвольные числа.
Например, полагая ![]() , получим одно из частных решений:
, получим одно из частных решений: ![]() .
.
Назад к разделу "1.7. Метод полного исключения неизвестных Жордана-Гаусса"