Сегодня вы изучите вопросы
-
Алгоритмы вычисления обратной матрицы
-
Алгоритмы определения ранга матрицы
Изучив тему занятия, вы сможете
-
находить обратную матрицу для данной квадратной матрицы;
-
находить решения любых систем линейных алгебраических уравнений.
Основные понятия
Известно, что число 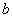 называется обратным к числу
называется обратным к числу 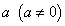 , если
, если 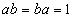 . Обратное число
. Обратное число 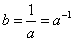 существует для любого числа, кроме нуля, и при этом является единственным. Аналогично введем для квадратных матриц понятие обратной матрицы
существует для любого числа, кроме нуля, и при этом является единственным. Аналогично введем для квадратных матриц понятие обратной матрицы , используемой обычно при решении систем линейных уравнений.
, используемой обычно при решении систем линейных уравнений.
Если две квадратные матрицы А и В одного и того же формата n таковы, что 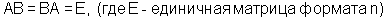 , то говорят, что матрицы А и В являются обратными друг другу, и используют обозначение
, то говорят, что матрицы А и В являются обратными друг другу, и используют обозначение 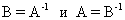 .
.
Таким образом, матрица 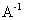 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 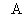 , если
, если 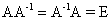 .
.
Выясним, какие матрицы имеют обратные матрицы, и если матрица А имеет обратную 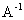 , то как ее находить.
, то как ее находить.
Квадратная матрица А называется вырожденной или особенной, если ее определитель равен нулю 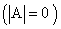 , в противном случае, то есть при
, в противном случае, то есть при 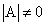 , матрица А называется невырожденной (неособенной).
, матрица А называется невырожденной (неособенной).
Нахождение обратных матриц опирается на следующую теорему, которую приведем без доказательства.
Теорема. Всякая невырожденная матрица имеет обратную, и притом единственную.
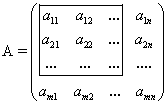
Пусть дана квадратная матрица формата n 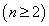
Приведем алгоритм вычисления обратной матрицы 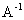 :
:
-
Составляем квадратную матрицу
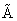 формата n следующим образом: на место каждого элемента поставим алгебраическое дополнение этого элемента, то есть
формата n следующим образом: на место каждого элемента поставим алгебраическое дополнение этого элемента, то есть -
Замечание. Полученная матрица
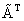 называется присоединенной
называется присоединенной или союзной матрицей
или союзной матрицей .
. -
Проверяем правильность вычислений, убедившись, что соотношение
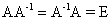 выполняется.
выполняется.
Пример. Дана матрица
-
Находим определитель матрицы А
-
Составляем квадратную матрицу
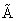 , для этого находим алгебраические дополнения элементов исходной матрицы:
, для этого находим алгебраические дополнения элементов исходной матрицы: -
Проведем проверку:
Пусть дана матрица, содержащая m строк и n столбцов:
Выделим в ней произвольным образом k строк и k столбцов, причем 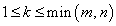 . Элементы выделенных строк и столбцов образуют квадратную матрицу порядка k.
. Элементы выделенных строк и столбцов образуют квадратную матрицу порядка k.
Определитель выделенной квадратной матрицы называется минором k-го порядка заданной матрицы А. В матрице А квадратиком выделен минор 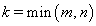 -го порядка.
-го порядка.
Количество комбинаций из k разных строк, отличающихся номером хотя бы одной строки, которые можно выделить из m строк заданной матрицы, определяется как число сочетаний из m элементов по k: 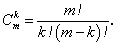 Аналогично из n столбцов заданной матрицы можно составить
Аналогично из n столбцов заданной матрицы можно составить 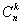 комбинаций по k. Следовательно, в прямоугольной матрице порядка
комбинаций по k. Следовательно, в прямоугольной матрице порядка 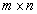 можно составить
можно составить 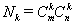 миноров k-го порядка.
миноров k-го порядка.
Наивысший порядок отличных от нуля миноров данной матрицы называется рангом матрицы А и обозначается r, r(A) или rang A.
Отличный от нуля минор наивысшего порядка называется базисным, а строки и столбцы, участвующие в образовании базисного минора, также называются базисными. Заметим, что базисных миноров у матрицы может оказаться больше чем один.
Из определения следует, что рангом обладает любая матрица, а ранг нулевой матрицы равен нулю. Если в матрице имеется хотя бы один отличный от нуля элемент, то ее ранг не меньше единицы. В случае, когда все миноры k-го и выше порядков равны нулю, 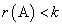 .
.
Отметим, что из свойств определителей следует, что ранг матрицы не изменяется:
-
при перестановке каких-либо строк (столбцов);
-
при умножении каждого элемента строки (столбца) на одно и тоже отличное от нуля число k;
-
при сложении элементов одной строки (одного столбца) с соответствующими элементами другой строки (другого столбца), умноженное на некоторое число
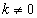 .
.
Ранг матрицы не изменяется и при элементарных преобразованиях матрицы.
Пример. Найти ранг матрицы:
Решение. Все миноры третьего порядка равны нулю. Имеется минор второго порядка, отличный от нуля 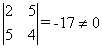 . Следовательно,
. Следовательно, 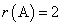 .
.
На практике определение ранга представляет собой трудоемкую операцию, поэтому, чтобы найти ранг матрицы, ее обычно приводят к виду, когда базисный минор становится очевидным. С этой целью применяют так называемые элементарные преобразования матриц. Элементарными преобразованиями матриц являются:
1) перестановка местами двух параллельных рядов матрицы;
2) умножение всех элементов ряда матрицы на одно и то же отличное от нуля число.
3) прибавление элементов какого-либо ряда матрицы к соответствующим элементам параллельного ряда, умноженных на одно и тоже не равное нулю число;
4) вычеркивание ряда матрицы, являющегося линейной комбинацией других параллельных ему рядов, в том числе состоящих из одних нулей.
Примечание. Матрица, полученная из данной с помощью элементарных преобразований, называется эквивалентной этой матрице. Эквивалентность матриц
этой матрице. Эквивалентность матриц обозначается знаком ~.
обозначается знаком ~.
С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
Ранг полученной ступенчатой матрицы равен p.
Пример. Найти ранг матрицы
Решение. Приведем матрицу А к ступенчатому виду с помощью элементарных преобразований:
Полученная ступенчатая матрица содержит три ненулевых строки, а это означает, что ее ранг равен 3. Следовательно, ранг исходной матрицы также равен 3.
Контрольные вопросы
-
Дайте определение обратной матрице. Всякая ли матрица имеет обратную?
-
Сформулируйте алгоритм нахождения обратной матрицы.
-
Что такое ранг матрицы? Каков смысл этого понятия?
-
Что называется базисным минором?
-
Изменится ли ранг матрицы при перестановке каких-либо строк
(столбцов)?
-
Изменится ли ранг матрицы при умножении каждого элемента строки (столбца) на одно и тоже отличное от нуля число?
-
Чему равен ранг нулевой матрицы?
-
Чему равен ранг ступенчатой матрицы?
-
Что Вы понимаете под элементарными преобразованиями?
-
Какая матрица называется эквивалентной по отношению к данной
матрице?
Задания для самостоятельной работы
Задание 1. Примеры для самоподготовки
(ранг матрицы, обратная матрица)
-
Найти ранг матриц:
-
Найти обратную матрицу для следующих матриц:
Задание 2. Примеры для самопроверки
(отметьте правильный вариант ответа)
-
Найти ранг матрицы
1) 0; 2) 1; 3) 2; 4) 3; 5) 4.
-
Найти ранг матрицы
1) 0; 2) 1; 3) 2; 4) 3; 5) 4.
-
Найти ранг матрицы
1) 0; 2) 1; 3) 2; 4) 3; 5) 4.
-
Найти ранг матрицы
1) 0; 2) 1; 3) 2; 4) 3; 5) 4.
-
5. Найти ранг матрицы
1) 0; 2) 1; 3) 2; 4) 3; 5) 4
-
Найти ранг матрицы
1) 0; 2) 1; 3) 2; 4) 3; 5) 4
-
Найти обратную матрицу для матрицы
-
Найти обратную матрицу для матрицы
-
Найти обратную матрицу для матрицы
-
Найти обратную матрицу для матрицы
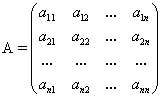 .
.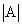 и убеждаемся, что
и убеждаемся, что 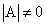 ;
;
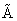
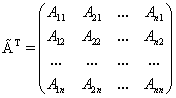 .
.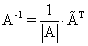 .
.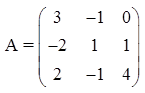 .
.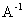 .
.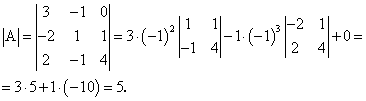
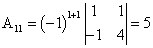 ;
; 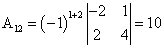 ;
;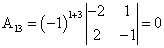 ;
; 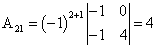 ;
;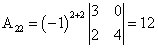 ;
; 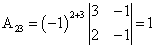 ;
;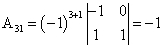 ;
; 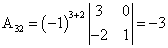 ;
;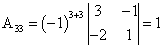 .
.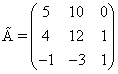
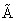
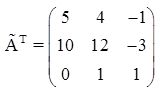
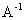
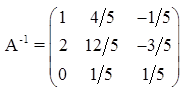
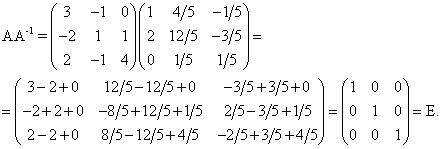
 .
.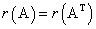 ;
;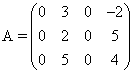 .
.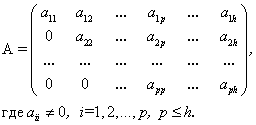
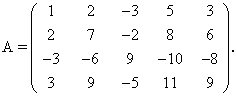
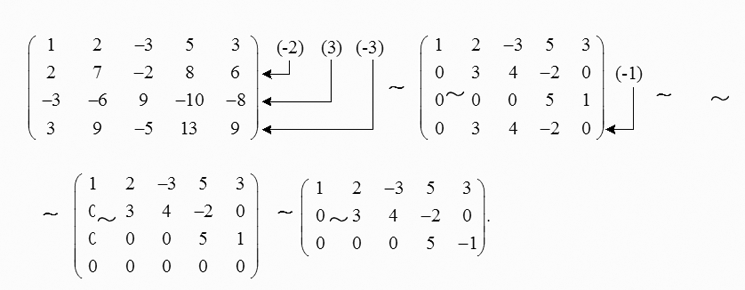
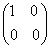
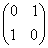
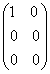
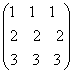
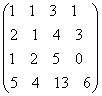
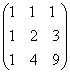
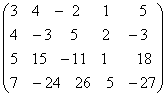
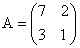
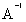 =
= 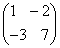 ;
;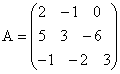
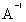 =
=  ;
;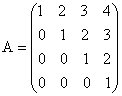
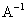 =
= 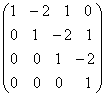 .
.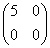
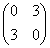
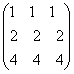

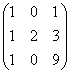
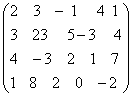
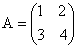
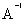 =
= 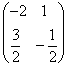 ;
;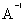 =
= 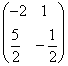 ;
;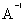 =
= 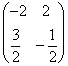 ;
;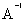 =
= 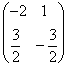 ;
;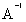 =
= 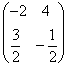 .
.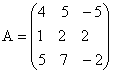
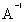 =
= 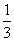
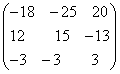 ;
;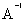 =
= 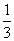
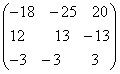 ;
;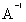 =
= 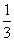
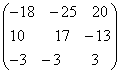 ;
;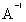 =
= 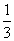
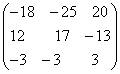 ;
;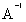 =
= 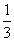
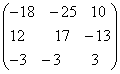 .
.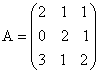
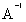 =
= 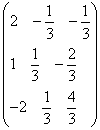 ;
;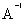 =
= 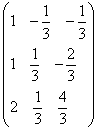 ;
;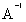 =
= 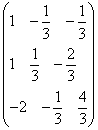 ;
;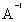 =
= 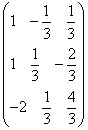 ;
;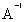 =
= 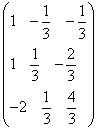 .
.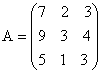
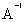 =
= 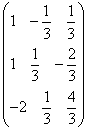 ;
;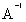 =
= 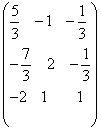 ;
;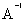 =
= 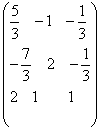 ;
;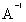 =
= 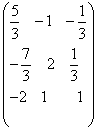 ;
;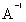 =
= 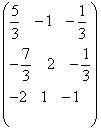 .
.
