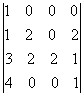
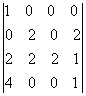
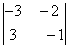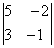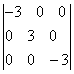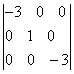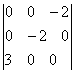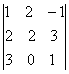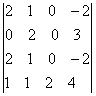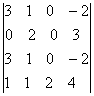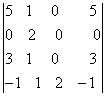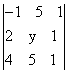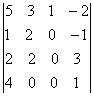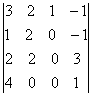Сегодня вы изучите вопросы
-
Определитель матрицы
-
Свойства определителей
-
Минор
-
Алгебраическое дополнение элемента матрицы
Изучив тему занятия, вы сможете
-
вычислять значения определителей любого порядка;
-
решать системы линейных уравнений.
Основные понятия
Понятие определителя вводится лишь для квадратных матриц. Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n–го порядка этой матрицы.
вводится лишь для квадратных матриц. Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n–го порядка этой матрицы.
Для записи определителя матрицы А используются следующие обозначения:  ,
,  ,
, 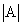 , или развернутое, учитывающее связь с элементами заданной матрицы
, или развернутое, учитывающее связь с элементами заданной матрицы  , где вертикальные линии вместо круглых (матричных) скобок указывают на то, что здесь речь идет об определителе матрицы А (о единственном числе), а не о таблице чисел.
, где вертикальные линии вместо круглых (матричных) скобок указывают на то, что здесь речь идет об определителе матрицы А (о единственном числе), а не о таблице чисел.
Числа 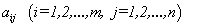 в этом случае называются элементами определителя
в этом случае называются элементами определителя . При этом, как и в матрице А, элементы
. При этом, как и в матрице А, элементы 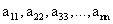 образуют главную диагональ определителя, а элементы
образуют главную диагональ определителя, а элементы  — побочную.
— побочную.
Введем понятие определителя сначала для квадратных матриц первого, второго и третьего порядка, а затем распространим на квадратные матрицы любого порядка.
Определителем матрицы 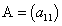 , то есть матрицы, состоящей из одного элемента
, то есть матрицы, состоящей из одного элемента 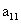 (определителем первого порядка), называется само число
(определителем первого порядка), называется само число 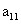 :
:
Пусть дана квадратная матрица второго порядка 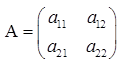 , тогда ее определителем (определителем второго порядка) называется число
, тогда ее определителем (определителем второго порядка) называется число
Пусть дана квадратная матрица третьего порядка 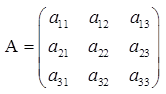 , тогда определителем третьего порядка данной матрицы называется число, которое вычисляется следующим образом:
, тогда определителем третьего порядка данной матрицы называется число, которое вычисляется следующим образом:
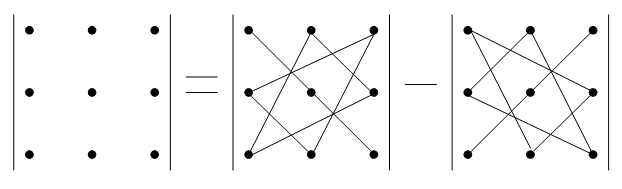
Замечание. При вычислении определителя третьего порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать следующим образом:
Пример. Вычислить определитель матрицы
Рассмотрим свойства определителей второго и третьего порядков.
Свойство 1. Определитель квадратной матрицы равен определителю ее транспонированной матрицы: 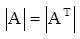 .
.
Докажем это свойство для определителя второго порядка. Действительно,
Свойство 2. При перестановке столбцов (строк) определитель меняет только знак.
Замечание. В дальнейшем для упрощения формулировок свойств определителей строки и столбцы матрицы будем называть рядами.
Свойство 3. Если какой-нибудь ряд матрицы является линейной комбинацией некоторых параллельных ему рядов, то определитель этой матрицы равен нулю. Действительно, пусть имеется следующая квадратная матрица третьего порядка: 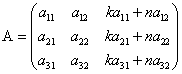 , тогда
, тогда
Следствие 1. Определитель, имеющий одинаковые параллельные ряды, равен нулю.
Следствие 2. Определитель, содержащий ряд из одних нулей, равен нулю.
Свойство 4. Если каждый элемент какого-либо ряда определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей, у одного из которых элементами соответствующего ряда являются первые слагаемые, у другого — вторые, а остальные элементы этих двух определителей те же, что у данного:
Свойство 5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Свойство 6. Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.
Действительно, на основании свойств 4 и 5
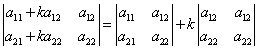 и, согласно следствию 1, второй определитель равен нулю, следовательно
и, согласно следствию 1, второй определитель равен нулю, следовательно 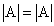 .
.
Для формулировки следующих свойств определителей возникает необходимость введения понятий минора и алгебраического дополнения
и алгебраического дополнения .
.
Введем понятие минора для элементов определителя третьего порядка. Пусть имеется определитель третьего порядка
Вычеркнем в ней 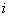 -ю строку и
-ю строку и 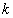 -ый столбец и сдвинем, не нарушая порядка, оставшиеся элементы. Определитель полученной матрицы 2-го порядка называется минором элемента
-ый столбец и сдвинем, не нарушая порядка, оставшиеся элементы. Определитель полученной матрицы 2-го порядка называется минором элемента 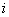 -ой строчки и
-ой строчки и 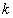 -го столбца матрицы А и обозначается
-го столбца матрицы А и обозначается 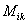 .
.
Например, минор элемента 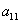 обозначают
обозначают  . Таким образом, по определению для определителя
. Таким образом, по определению для определителя
Введем понятие минора для определителя n-го порядка
Выделим в нем какой-либо элемент  и вычеркнем
и вычеркнем 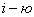 строку и
строку и 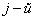 столбец, на пересечении которых расположен этот элемент. Полученный определитель (n-1)-го порядка называется минором
столбец, на пересечении которых расположен этот элемент. Полученный определитель (n-1)-го порядка называется минором  элемента
элемента 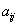
Алгебраическим дополнением элемента 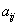 квадратной матрицы порядка n называется число, рассчитанное по формуле
квадратной матрицы порядка n называется число, рассчитанное по формуле 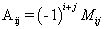 .
.
Согласно этой формуле, алгебраическое дополнение совпадает с минором 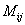 , если сумма индексов i + j является четным числом и имеет знак, противоположный знаку минора
, если сумма индексов i + j является четным числом и имеет знак, противоположный знаку минора 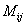 , если сумма индексов
, если сумма индексов 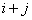 — нечетное число.
— нечетное число.
Формулы разложения
Теорема. Определитель третьего порядка равен сумме произведений элементов любого его ряда на соответствующие им алгебраические дополнения, то есть
Пример. Найти определитель
Данная теорема справедлива и для определителя n-го порядка. Определитель n-го порядка равен сумме произведений любого его ряда на соответствующие им алгебраические дополнения, то есть
Данные равенства называют разложениями определителя (формулами разложения) по
(формулами разложения) по 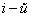 строке или по
строке или по 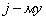 столбцу соответственно.
столбцу соответственно.
Все свойства, доказанные выше для определителей второго и третьего порядков, справедливы и для определителя n-го порядка.
В завершении приведем еще два важных свойства определителей.
Свойство 7. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Докажем данное свойство для определителя третьего порядка. С этой целью вычислим сумму произведений элементов первой строки матрицы на алгебраические дополнения соответствующих элементов третьей строки:
Свойство 8. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц.
Докажем это свойство для квадратных матриц второго порядка. Пусть
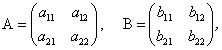 тогда с учетом свойств определителей
тогда с учетом свойств определителей
Контрольные вопросы
-
Для каких матриц применимо понятие определителя?
-
Что понимается под определителем?
-
Сформулируйте определение определителя второго и третьего порядков.
-
Проиллюстрируйте правило треугольников.
-
Что называется минором данного элемента определителя?
-
Что называется алгебраическим дополнением данного элемента определителя?
-
Какая связь между минором и алгебраическим дополнением данного элемента определителя?
-
Сформулируйте основные свойства определителей и проверьте их для определителей второго порядка.
-
В чем заключается выражение определителя непосредственно через его элементы?
-
Опишите основные методы вычисления определителей.
Задания для самостоятельной работы
Задание 1. Примеры для самоподготовки
(вычисление определителей, миноров, алгебраических дополнений)
-
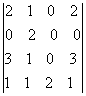
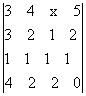
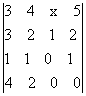
Вычислить определители:
-
Вычислить минор элемента
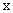 определителя
определителяОтвет. 3
-
Вычислить алгебраическое дополнение элемента
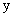 определителя
определителяОтвет. -5.
-
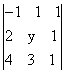
Используя свойства определителя, вычислить следующие определители:
-
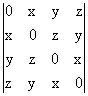
Найти выражение определителя
Задание 2. Примеры для самопроверки
(отметьте правильный вариант ответа)
-
Вычислить определитель
1) 0; 2) -1; 3) 1; 4) 9; 5) -11.
-
Вычислить определитель
1) 0; 2) -1; 3) 1; 4) 11; 5) -11.
-
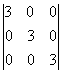
Вычислить определитель
1) 3; 2) -3; 3) 9; 4) -9; 5) 27.
-
Вычислить определитель
1) 3; 2) -3; 3) 9; 4) -9; 5) 27.
-
Вычислить определитель
1) 12; 2) 7; 3) -12; 4) -7; 5) 8.
-
Вычислить определитель
1) 12; 2) 7; 3) -12; 4) -3; 5) 8.
-
Вычислить определитель
1) 6; 2) 12; 3) -12; 4) 8; 5) 14
-
Вычислить определитель
1) 6; 2) 12; 3) 22; 4) 8; 5) 14.
-
Вычислить определитель
1) -2; 2) 4; 3) 7; 4) -5; 5) 0.
-
Вычислить определитель
1) -2; 2) 0; 3) 7; 4) -5; 5) 10.
-
Вычислить определитель
1) 1; 2) -1; 3) 2; 4) 0; 5) -2.
-
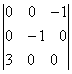
Вычислить определитель
1) 0; 2) -1; 3) 2; 4) 11; 5) -2.
-
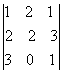
Вычислить минор элемента
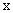 определителя
определителя1) 0; 2) -2; 3) 2; 4) 4; 5) 6.
-
Вычислить минор элемента
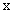 определителя
определителя1) 0; 2) 2; 3) -2; 4) 4; 5) 6.
-
Вычислить алгебраическое дополнение элемента
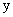 определителя
определителя1) 0; 2) 1; 3)-1; 4) 2; 5) -5.
-
Вычислить алгебраическое дополнение элемента
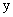 определителя
определителя1) 0; 2) 1; 3)-1; 4) 2; 5) -5.
-
Используя свойства определителя, вычислить определитель:
1) 4; 2) 0; 3) 6; 4) 2; 5) -7.
-
Используя свойства определителя, вычислить определитель:
1) 1; 2) 0; 3) 6; 4) 2; 5) 4.
-
Используя свойства определителя, вычислить определитель:
1) 10; 2) 20; 3) 30; 4) 40; 5) 50
-
Используя свойства определителя, вычислить определитель:
1) 1; 2) 10; 3) 20; 4) 30; 5) 50.
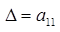 .
. .
.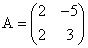 .
.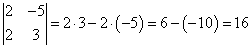
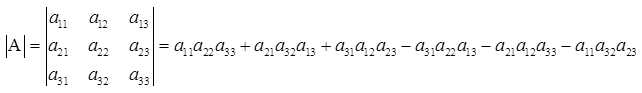
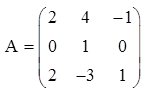
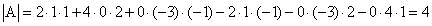 .
.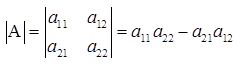 ,
,  , то есть
, то есть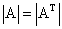 .
.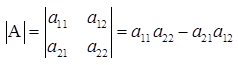 , то
, то
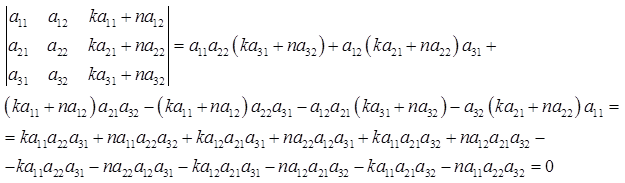
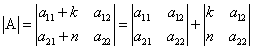 .
.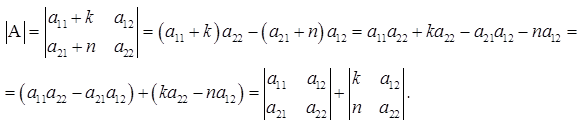
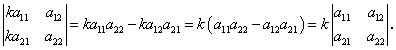
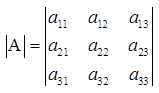 .
.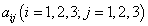 .
.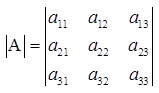
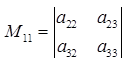 ,
, 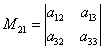 ,
, 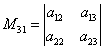 ,
, 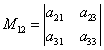 и т.д.
и т.д.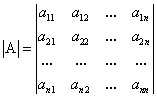 .
.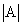 .
.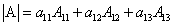 ;
; ;
;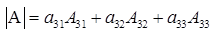 ;
;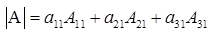 ;
;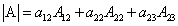 ;
;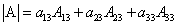 .
.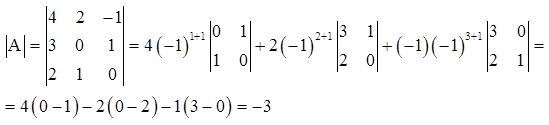
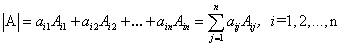 ;
;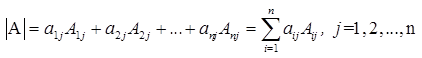 .
.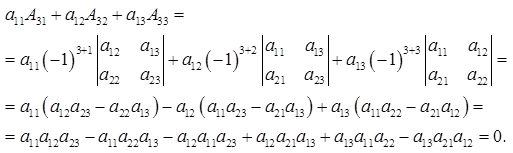
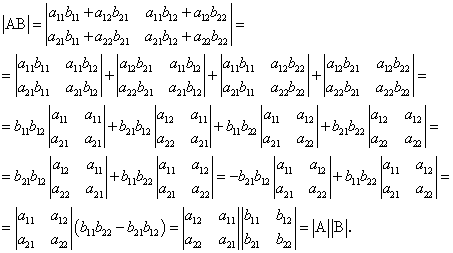
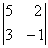
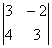
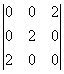
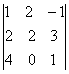
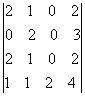
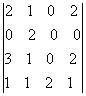
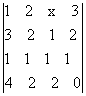 .
.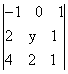 .
.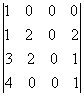 ;
;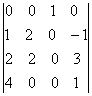 .
. .
.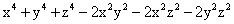 .
.