Сегодня вы изучите вопросы
-
Основы линейной алгебры
-
Основные понятия линейной алгебры
-
Понятие матрицы
Изучив тему занятия, вы сможете
-
умножать матрицу на число;
-
производить линейные операции над матрицами;
-
умножать матрицы;
-
возводить матрицы в натуральную степень.
Элементы линейной алгебры широко используются при решении большого числа прикладных экономических и управленческих задач. Успешное усвоение основных понятий данного занятия является основой для ее применения.
Основные понятия
Матрицей размера
размера 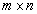 называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы
называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы .
.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,…, X, Y, Z, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией:  , где
, где
Например, матрица размеров 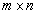 имеет вид:
имеет вид:
или в сокращенной записи
Например, матрица размеров 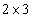 имеет вид:
имеет вид:
Наряду с круглыми скобками для обозначения матриц используются
Две матрицы А и В одинаковой размерности 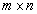 называются равными, если
называются равными, если  при всех
при всех 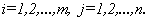
Виды матриц
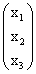
Матрица, состоящая из одного столбца, называется матрицей (вектором)-столбцом и обозначается
и обозначается  , а состоящая из одной строки — матрицей (вектором)-строкой
, а состоящая из одной строки — матрицей (вектором)-строкой , соответственно обозначается
, соответственно обозначается  .
.
Матрица называется квадратной n-го порядка , если число ее строк равно числу столбцов и равно n:
, если число ее строк равно числу столбцов и равно n:
Элементы 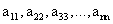 образуют главную диагональ квадратной матрицы порядка n, а элементы
образуют главную диагональ квадратной матрицы порядка n, а элементы  — побочную диагональ.
— побочную диагональ.
Например,
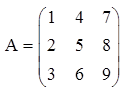 — квадратная матрица третьего порядка, элементами главной диагонали являются числа 1, 5, 9, а побочной — 7, 5 ,3.
— квадратная матрица третьего порядка, элементами главной диагонали являются числа 1, 5, 9, а побочной — 7, 5 ,3.
Если все элементы, кроме элементов, образующих главную диагональ квадратной матрицы, равны нулю, то такая матрица называется диагональной .
.
Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка и обозначается буквой Е.
и обозначается буквой Е.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О. Нулевая матрица имеет следующий вид:
и обозначается буквой О. Нулевая матрица имеет следующий вид:
В линейной алгебре матрицы Е и О играют такую же роль, какую играют числа 1 и 0 в арифметике.
Матрица, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается
к данной и обозначается 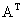 .
.
Транспонированная матрица обладает следующим свойством: 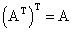 .
.
Умножение матрицы на число
Пусть 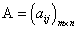 — произвольная матрица,
— произвольная матрица, 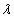 — произвольное действительное число.
— произвольное действительное число.
Произведением матрицы А на число 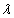 называется новая матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число
называется новая матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число 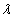 , т.е.
, т.е.
Таким образом, можно выделить следующее следствие.
Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Сложение и вычитание матриц
Эта операция определяется только для матриц одинаковой размерности (формата).
Суммой двух матриц А и В одинаковой размерности называется новая матрица С того же размера, каждый элемент которой равен сумме соответствующих (стоящих на одинаковых местах) элементов данных матриц.
Например, пусть А и В — матрицы размерности 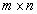 . Тогда по определению под суммой
. Тогда по определению под суммой 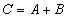 понимается
понимается
Вышеприведенные действия над матрицами называются линейными .
.
Линейные операции над матрицами обладают следующими свойствами.
обладают следующими свойствами.
-
Переместительность (коммутативность) умножения матрицы на число
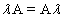 .
. -
Распределительность (дистрибутивность) сложения матриц относительно умножения на число
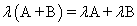 .
. -
Распределительность (дистрибутивность) относительно сложения чисел
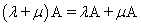 .
.
Таким образом, линейные операции над матрицами можно выполнять по аналогии с привычными правилами алгебры чисел.
Вычитание для матриц (как и для чисел) определяется как действие, обратное сложению. Разностью матриц А и В(А — В) одинаковой размерности называется такая матрица С, что
В + С = А.
Легко заметить, что матрица С, удовлетворяющая этому условию, всегда существует, и притом только одна. Ее элементы определяются равенствами
Таким образом, при вычитании матриц вычитаются соответствующие элементы этих матриц.
Замечание. Знаки сравнения (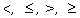 ) для матриц любого формата лишены смысла.
) для матриц любого формата лишены смысла.
Умножение матриц
Умножение матрицы А на матрицу В (рассматриваются именно в таком порядке) определено, если число столбцов первой матрицы равно числу строк второй матрицы. В этом случае матрица А называется согласованной с матрицей В.
Иначе говоря, если порядок матрицы А равен 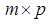 , то порядок согласованной с ней матрицы В должен быть
, то порядок согласованной с ней матрицы В должен быть 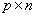 , где
, где 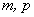 — любые натуральные числа.
— любые натуральные числа.
Произведением матрицы 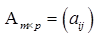 на матрицу
на матрицу 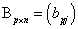 называется такая матрица
называется такая матрица 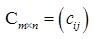 , что
, что
Таким образом, для вычисления элемента 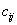 , стоящего в
, стоящего в 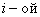 строке и в
строке и в 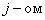 столбце матрицы С, следует каждый элемент
столбце матрицы С, следует каждый элемент 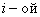 строки матрицы А умножить на соответственный элемент
строки матрицы А умножить на соответственный элемент 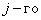 столбца матрицы В и результат сложить.
столбца матрицы В и результат сложить.
Примеры:
Умножение матриц обладает следующими свойствами:
Заметим, что умножение матриц некоммутативно: 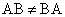 .
.
Выше было определено, что операция умножения имеет место только для согласованных матриц А и В, при этом матрицы, взятые в ином порядке (В и А), могут оказаться несогласованными, тогда их произведение не определено. Но даже в том случае, когда согласованность матриц не нарушается, произведения АВ и ВА могут оказаться разными.
Например, для матриц
Если АВ = ВА, то матрицы А и В называются перестановочными (коммутирующими). Очевидно, это может иметь место только в том случае, когда А и В — квадратные матрицы одного и того же порядка.
Например, коммутирующими являются матрицы
Действительно,
то есть для данных матриц АВ = ВА.
Еще одно замечание: произведение двух матриц может быть нуль-матрицей, даже если ни один из сомножителей не является нуль-матрицей.
Например, пусть даны матрицы 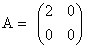 и
и 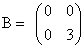 . Найдем произведение АВ и ВА:
. Найдем произведение АВ и ВА:
Отсюда следует, что умножение матриц обладает рядом свойств, не характерных для умножения действительных чисел, поэтому при действиях с матрицами необходимо проявлять осмотрительность и аккуратность.
В заключение, отметим свойства, присущие операции транспонирования:
Возведение в степень
На основе определения произведения матриц умножать матрицу А на себя можно только в том случае, если это квадратная матрица.
Пусть k — целое неотрицательное число, тогда k-й степенью квадратной матрицы А называется матрица, которая вычисляется следующим образом:
Контрольные вопросы
-
Что называется матрицей? Перечислите виды матриц.
-
Какую роль в линейной алгебре играют единичная и нулевая матрицы?
-
Какая матрица называется диагональной?
-
Дайте определение квадратной матрицы.
-
Какая матрица называется транспонированной по отношению к данной?
-
Для каких матриц определена операция сложения?
-
Перечислите основные свойства сложения матриц.
-
Какие матрицы называются коммутирующими между собой?
-
Для каких матриц определена операция умножения?
-
Перечислите основные свойства умножения матриц.
Задания для самостоятельной работы
Задание 1. Примеры для самоподготовки
(действия над матрицами)
-
Найти сумму матриц
-
Найти сумму матриц
-
Найти сумму матриц
-
Найти разность матриц
-
Найти разность матриц
-
Найти произведение действительного числа на матрицу
-
Найти произведение действительного числа на матрицу
-
Найти произведение матриц
-
Найти произведение матриц
-
Найти произведение матриц
Задание 2. Примеры для самопроверки
(отметьте правильный вариант ответа)
-
Найти сумму матриц
-
Найти сумму матриц
-
Найти сумму матриц
-
Найти разность матриц
-
Найти разность матриц
-
Найти разность матриц
-
Найти произведение действительного числа на матрицу
-
Найти произведение действительного числа на матрицу
-
Найти произведение действительного числа на матрицу
-
Найти произведение матриц
-
Найти произведение матриц
-
Найти произведение матриц
-
Найти произведение матриц
-
Найти произведение матриц
-
Найти произведение матриц
-
Найти произведение матриц
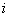 — номер строки;
— номер строки;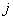 — номер столбца.
— номер столбца.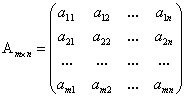
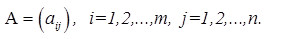
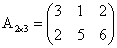 .
.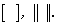
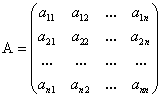 .
.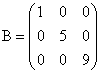 — диагональная матрица третьего порядка.
— диагональная матрица третьего порядка.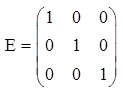 — единичная матрица третьего порядка.
— единичная матрица третьего порядка.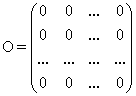 .
.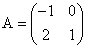 , то
, то 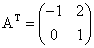 .
.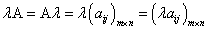 .
.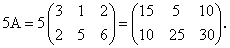
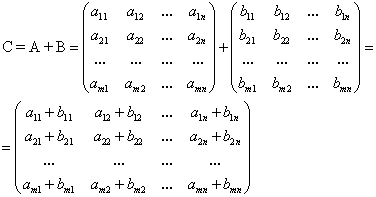
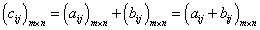 .
.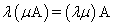 .
.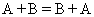 .
.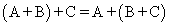 .
.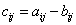 .
.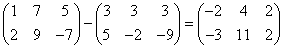 .
.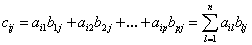 , где
, где 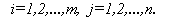
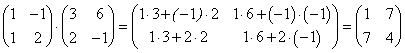 .
.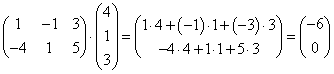 .
.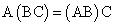 ;
;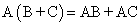 ;
;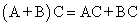 ;
;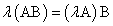 .
.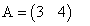 и
и 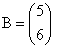 имеем:
имеем: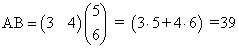 , но
, но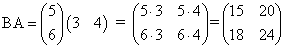 .
.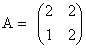 и
и 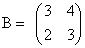 .
.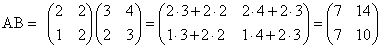
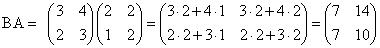 ,
,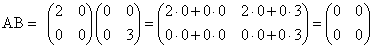 ;
;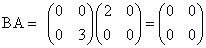 .
.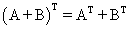 ;
;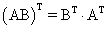 ;
;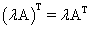 .
.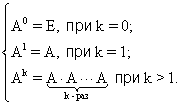
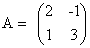 .
.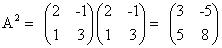 ;
;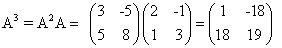 .
.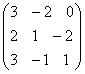 +
+ 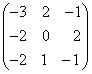
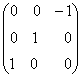
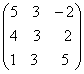 +
+ 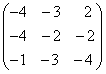
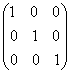
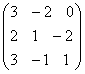 +
+ 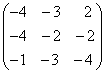
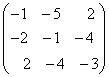
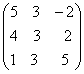 —
— 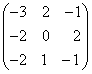
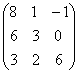
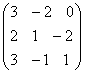 —
— 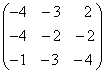
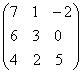
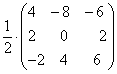
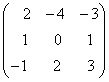
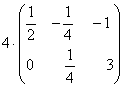
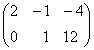
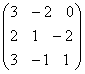 ∙
∙ 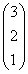

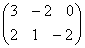 ∙
∙ 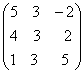
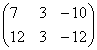
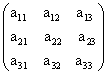 ∙
∙ 
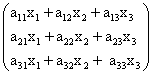
 +
+ 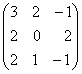
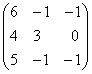 ;
;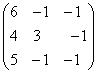 ;
;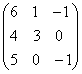 ;
;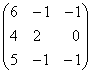 ;
;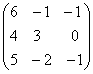
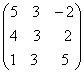 +
+ 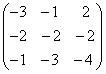
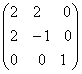 ;
;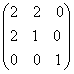 ;
;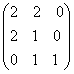 ;
;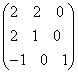 ;
;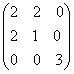 .
.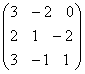 +
+ 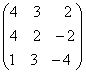
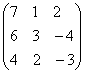 ;
;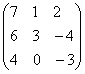 ;
;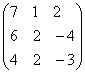 ;
;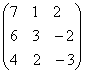 ;
;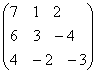
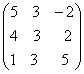 —
— 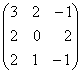
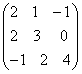 ;
;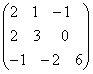 ;
;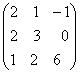
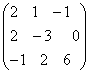 ;
;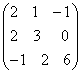
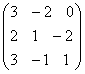 —
— 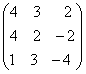
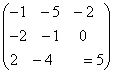 ;
;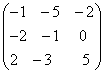 ;
;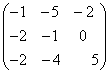 ;
;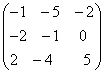 ;
;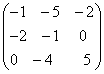 .
.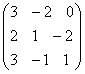 —
— 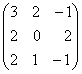
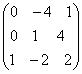 ;
;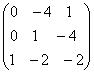 ;
;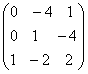 ;
;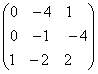 ;
;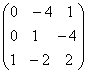 .
.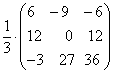
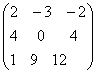 ;
;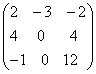 ;
;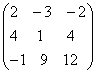 ;
;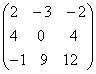 ;
;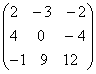 .
.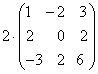
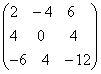 ;
;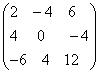 ;
;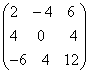 ;
;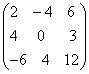 ;
;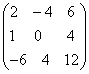 .
.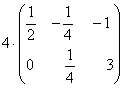
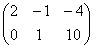 ;
;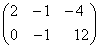 ;
;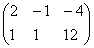 ;
;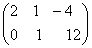 ;
;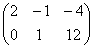 .
.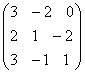 ∙
∙ 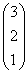
 ;
; ;
; ;
;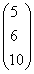 ;
; .
.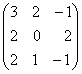 ∙
∙ 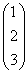
 ;
;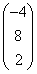 ;
; ;
; ;
;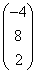 .
.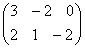 ∙
∙ 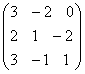
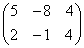 ;
;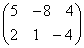 ;
;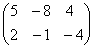 ;
;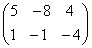 ;
;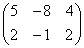 .
.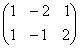 ∙
∙ 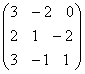
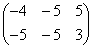 ;
;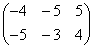 ;
;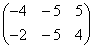 ;
;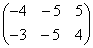 ;
;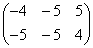 .
.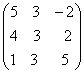 ∙
∙ 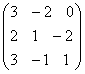
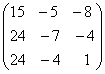 ;
;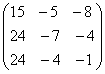 ;
;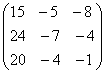 ;
;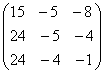 ;
;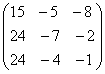 .
.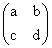 ∙
∙ 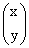
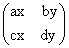 ;
;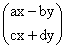 ;
;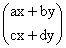 ;
;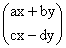 ;
;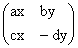 .
.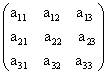 ∙
∙ 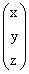 :
: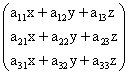 ;
;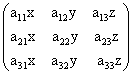 ;
;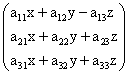 ;
;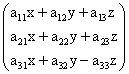 ;
;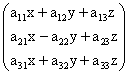 .
.
