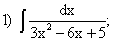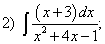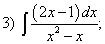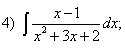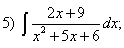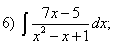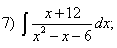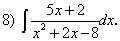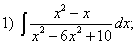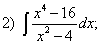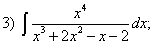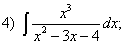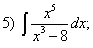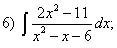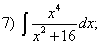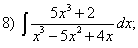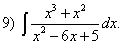Сегодня вы изучите вопросы
-
Метод интегрирования неопределенного интеграла по частям
-
Интегрирование рациональных дробей
-
Интегрирование некоторых классов тригонометрических функций
-
Интегрирование иррациональных функций
Изучив тему занятия, вы сможете
-
найти нетабличные неопределенные интегралы;
-
найти интегралы от рациональных дробей;
-
найти интегралы от некоторых классов тригонометрических функций;
-
найти интегралы от иррациональных функций.
Основные понятия
Пусть u и v — две дифференцируемые функции одного и того же аргумента.
Известно, что:
Возьмем от обеих частей равенства (177) неопределенный интеграл :
:
Отсюда находим:
Равенство (178) называется формулой интегрирования неопределенного интеграла по частям.
Если подынтегральные выражения в равенстве (178) рассматривать как произведение двух сомножителей, то формула интегрирования по частям переводит один интеграл в другой, где дифференцирование от одного множителя подынтегрального выражения переведено на другой множитель.
Действительно, подынтегральное выражение интеграла слева в равенстве (178) равно 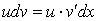 , а подынтегральное выражение интеграла правой части равенства (178) равно
, а подынтегральное выражение интеграла правой части равенства (178) равно 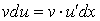 .
.
Следует заметить, что разбиение подынтегрального выражения должно быть таким, чтобы интегрирование дифференциала 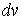 не представляло трудностей и чтобы замена
не представляло трудностей и чтобы замена 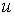 на
на 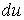 и
и 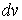 на
на 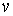 в итоге упрощала подынтегральное выражение.
в итоге упрощала подынтегральное выражение.
Приведем некоторые типы интегралов, которые удобно раскрывать методом интегрирования по частям:
-
В этом случае удобно положить
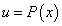 , а остаток подынтегрального выражения обозначить dv.
, а остаток подынтегрального выражения обозначить dv. -
В этом случае удобно положить
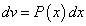 , а остаток подынтегрального выражения принять за u.
, а остаток подынтегрального выражения принять за u. -
В этом случае можно принять за
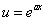 и повторно интегрировать по частям.
и повторно интегрировать по частям.
Замечание. В первом случае формулу интегрирования по частям применяют n раз, понижая каждый раз показатель степени многочлена на единицу.
Ко второму случаю можно отнести также интегралы, у которых отсутствует многочлен, а аргументы логарифмической или обратных тригонометрических функций более сложные.
Рассмотрим конкретные примеры применения метода интегрирования по частям.
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Пример 5.
Пусть 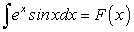 . В этом обозначении равенство
. В этом обозначении равенство
перепишем так:
то есть относительно F(x) мы получили линейное уравнение.
Отсюда находим:
Возвращаясь к прежнему обозначению, окончательно находим:
Под рациональной дробью понимается отношение двух многочленов:
понимается отношение двух многочленов:
х — независимая переменная,
Если 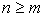 , то дробь (179) является неправильной. В этом случае делением числителя на знаменатель дробь (179) можно представить в виде суммы целого многочлена и правильной рациональной дроби.
, то дробь (179) является неправильной. В этом случае делением числителя на знаменатель дробь (179) можно представить в виде суммы целого многочлена и правильной рациональной дроби.
Следовательно, дробь 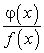 можно представить в следующем виде:
можно представить в следующем виде:
В дальнейшем будем полагать, что дробь (179) является правильной и несократимой.
По основной теореме алгебры корнями (или нулями) многочлена
(или нулями) многочлена 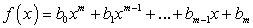 являются либо действительные числа, либо комплексные (сопряженные) числа, суммарное число корней равно степени многочлена, причем каждый корень считается столько раз, какова его кратность.
являются либо действительные числа, либо комплексные (сопряженные) числа, суммарное число корней равно степени многочлена, причем каждый корень считается столько раз, какова его кратность.
По теореме Безу, если x = a является нулем многочлена f (x), то справедливо равенство 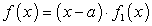 , где
, где 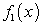 — многочлен, степень которого на единицу меньше степени f (x).
— многочлен, степень которого на единицу меньше степени f (x).
Также легко доказать, что если f (x) имеет комплексный корень 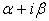 , то он имеет и сопряженный корень
, то он имеет и сопряженный корень 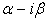 .
.
Следовательно, по теореме Безу f (x) можно представить в виде:
Действительно, перемножив линейные множители 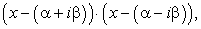 получим квадратный трехчлен с действительными коэффициентами. Покажем это:
получим квадратный трехчлен с действительными коэффициентами. Покажем это:
То есть 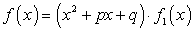 , где
, где 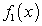 — многочлен, степень которого на две единицы меньше, чем степень f (x).
— многочлен, степень которого на две единицы меньше, чем степень f (x).
Отсюда следует по основной теореме алгебры, что всякий многочлен степени n можно представить так:
В этой связи рациональную дробь 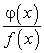 можно рассматривать как отношение
можно рассматривать как отношение
Рассмотрим частный случай, когда
Покажем, что в этом случае правильную рациональную дробь 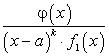 можно представить в следующем виде:
можно представить в следующем виде:
где A1 — действительное число, отличное от нуля;
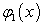 — многочлен, степень которого меньше степени знаменателя
— многочлен, степень которого меньше степени знаменателя 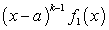 .
.
Действительно,
Подберем такое 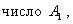 чтобы многочлен
чтобы многочлен 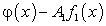 в точке x = a обратился в нуль:
в точке x = a обратился в нуль:
Таким образом, если 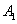 определить равенством (180), то по теореме Безу
определить равенством (180), то по теореме Безу 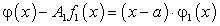 .
.
Отсюда находим, что:
или
Применяя заданное разложение повторно 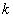 раз, получим:
раз, получим:
По аналогии, если 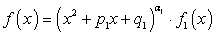 , то получим:
, то получим:
где 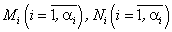 являются действительными числами. Таким образом, правильную несократимую рациональную дробь, знаменатель которой имеет действительные и комплексные корни, можно представить в следующем виде:
являются действительными числами. Таким образом, правильную несократимую рациональную дробь, знаменатель которой имеет действительные и комплексные корни, можно представить в следующем виде:
Из разложения (182) следует, что интегрирование правильной несократимой рациональной дроби всегда можно привести к интегрированию рациональных дробей следующих видов:
называемых простейшими.
Перейдем к интегрированию простейших рациональных дробей.
Интеграл (183) берется методом понижения порядка, по так называемой рекуррентной формуле, основная идея которой заключается в выражении интеграла (183) аналогичным интегралом, степень знаменателя которого будет меньше на единицу (183).
Имеем:
Второй интеграл в равенстве (184) возьмем по частям:
Равенство (183) с учетом полученного равенства (185) перепишется так:
Применяя формулу (186) последовательно k — 1 раз, придем к интегралу:
Подставляя затем вместо t и а их соответствующие выражения, получим выражение интеграла (183) через действительные числа M, N, p и q.
Примеры.
-
Отсюда находим, что
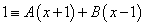 . Ввиду тождественности последнего равенства положим
. Ввиду тождественности последнего равенства положим 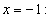
Пусть
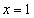 , получим
, получим 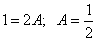 . Следовательно, заданный интеграл можно разбить на два интеграла:
. Следовательно, заданный интеграл можно разбить на два интеграла:Заданный интеграл можно раскрыть, если воспользоваться табличным интегралом
-
Воспользуемся табличным интегралом:
Имеем:
-
Для раскрытия последнего интеграла воспользуемся табличным интегралом:
-
Рассмотрим интеграл:
Так как все тригонометрические функции рационально выражаются через синус и косинус, следовательно, всякая функция, рационально зависящая от тригонометрических функций, может быть преобразована в соответствующую рациональную функцию только синуса и косинуса.
только синуса и косинуса.
Поэтому достаточно будет рассмотреть интегрирование функций, рационально зависящих от синуса и косинуса.
Рассмотрим интеграл:
где 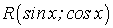 является рациональной функцией
является рациональной функцией 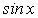 и
и 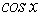 .
.
Интегралы типа (188) называются тригонометрическими интегралами .
.
Интеграл (188) приводится к интегралу от рациональной функции переменной 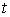 при помощи универсальной подстановки:
при помощи универсальной подстановки:
Действительно, если воспользоваться известными из школьного курса тригонометрическими формулами, то легко выразить 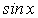 ,
, 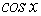 и
и 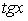 через переменную
через переменную 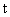 :
:
Подставляя найденные выражения 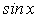 и
и 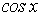 ,
, 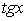 и
и 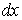 в выражение подынтегральной функции (1), получим интеграл от рациональной функции переменной
в выражение подынтегральной функции (1), получим интеграл от рациональной функции переменной 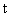 :
:
Пример.
В некоторых частных случаях быстрее приводят к цели другие подстановки, так как универсальная подстановка на практике в большинстве случаев приводит к интегрированию сложных рациональных дробей.
Рассмотрим следующие частные случаи.
-
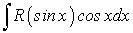 , где
, где 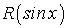 является рациональной функцией
является рациональной функцией 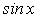 .
.Подстановка
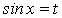 приводит этот интеграл к интегралу от рациональной функции переменной
приводит этот интеграл к интегралу от рациональной функции переменной 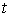 :
: 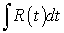
Пример.
-
Подстановка
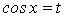 приводит этот интеграл к интегралу от рациональной функции переменной
приводит этот интеграл к интегралу от рациональной функции переменной 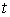 :
: 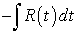 .
.Пример.
-
Подстановкой
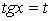 данный интеграл сводится к интегралу от рациональной функции переменной
данный интеграл сводится к интегралу от рациональной функции переменной 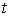 :
:Пример.
-
где подынтегральная функция является рациональной функцией от четных степеней синуса и косинуса переменной интегрирования.
Заданный интеграл приводится к интегралу от рациональной функции переменной
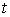 подстановкой
подстановкой 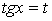 :
:Пример.
Рассмотрим наиболее распространенные неопределенные интегралы от иррациональных функций , которые с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, выражаются через элементарные функции.
, которые с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, выражаются через элементарные функции.
-
Интегралы, подынтегральные функции которых содержат различные радикалы переменной
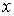 :
:где
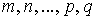 являются целыми положительными числами.
являются целыми положительными числами.Заданный интеграл приводится к интегралу от рациональной функции с помощью замены переменной
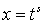 , где
, где 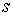 — общий знаменатель всех показателей степеней.
— общий знаменатель всех показателей степеней.Пример.
-
Интегралы, содержащие различные радикалы от дробно-линейной функции.
Дробно-линейной функцией
 от переменной
от переменной 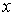 называется функция от дроби
называется функция от дроби 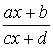 , где
, где 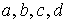 — действительные числа. Следовательно, мы рассматриваем интегралы следующего типа:
— действительные числа. Следовательно, мы рассматриваем интегралы следующего типа:где
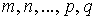 являются целыми положительными числами.
являются целыми положительными числами.Данные интегралы приводятся к интегралам от рациональной дроби путем подстановки
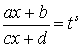 , где
, где 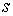 — общий знаменатель всех показателей степеней.
— общий знаменатель всех показателей степеней.
Пример.
Рассмотрим интегралы от иррациональной функции, которые приводятся к рациональным функциям с помощью замены переменной и подстановки. Данные интегралы нами приведены как табличные.
В правой части последнего равенства мы имеем исходный интеграл. Переносом этого интеграла в левую часть окончательно находим:
Для привития навыков интегрирования рассмотрим дополнительный перечень интегралов, заданных не по типам, чтобы в каждом конкретном случае читатель мог сам выбрать тот или иной эффективный способ интегрирования.
Пример 1.
Пример 2.
Пример 3.
Последнее вытекает из табличного интеграла 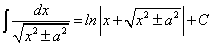 .
.
Пример 4.
Пример 5.
Пример 6.
Пример 7.
Рассмотрим пример, где потребуется дважды применять интегрирование по частям.
Пример 8.
Пример 9.
Пример 10.
Пример 11.
Пример 12.
В числителе выделим дифференциал знаменателя:
Пример 13.
Полагаем х = 2: 2 = — А; А = — 2.
Полагаем х = 3: 3 = В.
Следовательно, заданный интеграл можно переписать так:
Пример 14.
Разложим знаменатель на линейные множители:
Представим рациональную дробь 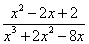 в виде трех слагаемых с линейными знаменателями:
в виде трех слагаемых с линейными знаменателями:
Отсюда, полагая х = 0, получим: 2 = -8А; 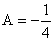 .
.
Полагая х = 2, получим: 4 — 4 + 2 = 12В; 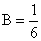 .
.
Полагая х = -4, получим: 16 + 8 + 2 = 24С; 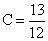 .
.
Отсюда находим, что:
Пример 15.
Для раскрытия последнего интеграла воспользуемся табличным интегралом:
В нашем случае а = 6; u = х — 5. Имеем:
Пример 16.
В заключение остановимся на понятии «неберущиеся интегралы» . Как известно, интегралы от непрерывных функций существуют. Однако этим не утверждается, что первообразная непременно будет одна из основных элементарных функций или функция, полученная из элементарных функций путем всевозможных комбинаций образования сложных функций. Весьма вероятно, что произвольно взятый нами интеграл может иметь первообразную, которая не является элементом известного нам множества функций. Например, первообразные интегралы
. Как известно, интегралы от непрерывных функций существуют. Однако этим не утверждается, что первообразная непременно будет одна из основных элементарных функций или функция, полученная из элементарных функций путем всевозможных комбинаций образования сложных функций. Весьма вероятно, что произвольно взятый нами интеграл может иметь первообразную, которая не является элементом известного нам множества функций. Например, первообразные интегралы
не могут быть образованы из основных элементарных функций и любого способа образования сложных функций. В этом случае говорят, что интеграл является неберущимся. По сути дела, приведенные интегралы это абсолютно новые функции.
Контрольные вопросы
-
Какие вы знаете методы интегрирования и в чем заключается идея этих методов?
-
В чем заключается различие метода замены переменной от метода подстановки?
-
Как вы понимаете понятие «неберущиеся интегралы»?
-
Каким условиям должна удовлетворять подынтегральная функция, чтобы существовал неопределенный интеграл (или первообразная)?
-
Напишите формулу интегрирования по частям для неопределенного интеграла.
-
Какие дроби называются простейшими рациональными дробями и чему равны интегралы от таких функций?
Задания для самостоятельной работы
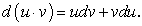 (177)
(177)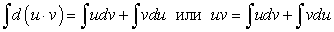 .
.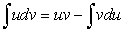 . (178)
. (178)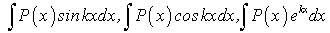 ,
,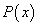 — многочлен,
— многочлен, 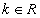 .
.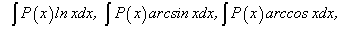
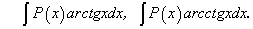
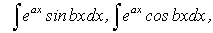 где
где 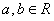 .
.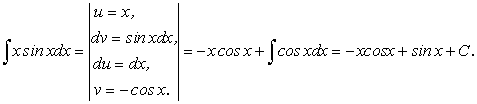
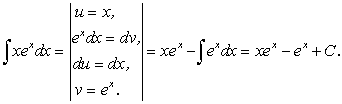
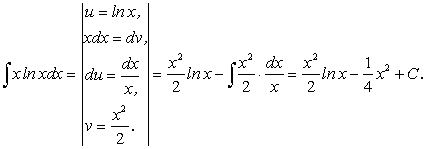
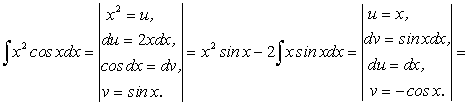
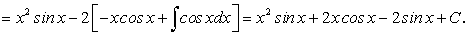
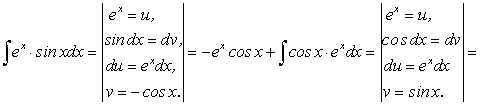
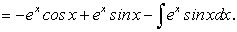
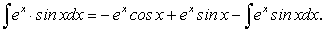
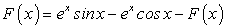 ,
,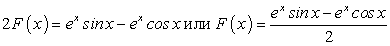 .
.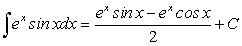 .
.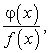 (179)
(179)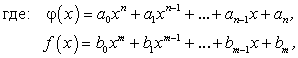
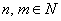 ,
, 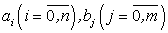 — действительные числа.
— действительные числа.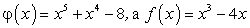 .
.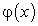 на
на 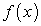 , будем иметь:
, будем иметь: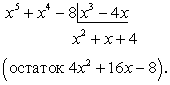
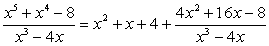 .
.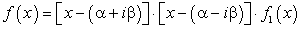 .
.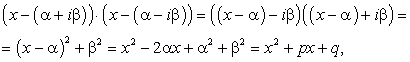
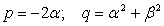 .
.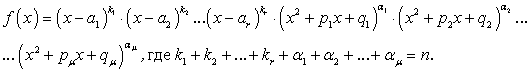
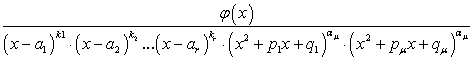 .
.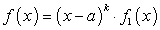 .
.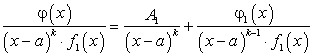 ,
,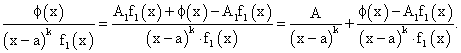
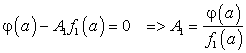 . (180)
. (180)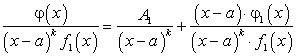 ,
,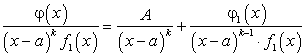 . (181)
. (181)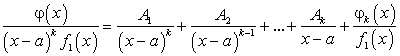 .
.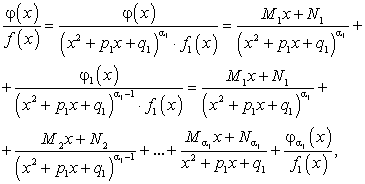
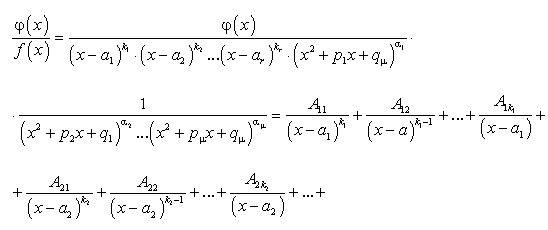
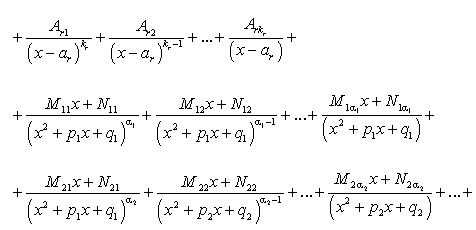
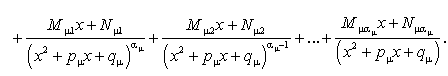 (182)
(182)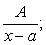
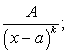
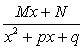 ;
;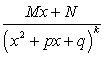 ,
,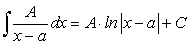 .
.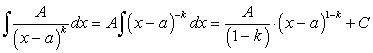 .
.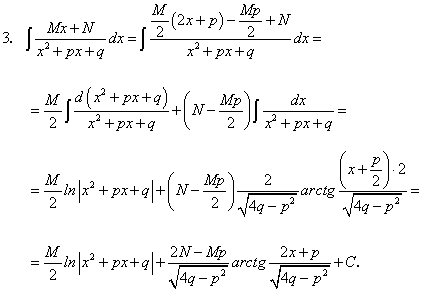
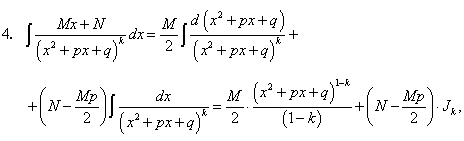
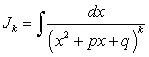 . (183)
. (183)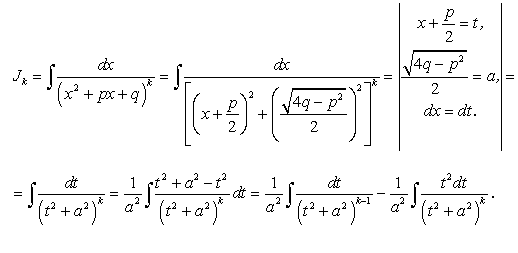 (184)
(184)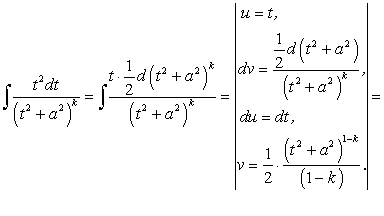
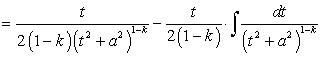 . (185)
. (185)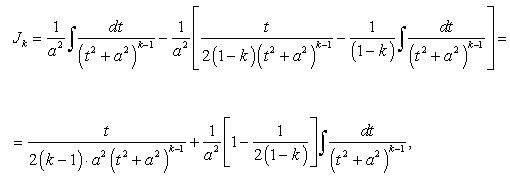
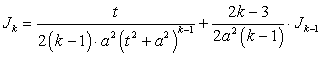 . (186)
. (186)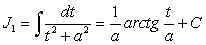 . (187)
. (187)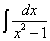 .
.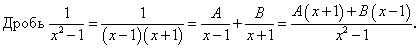
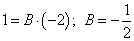 .
.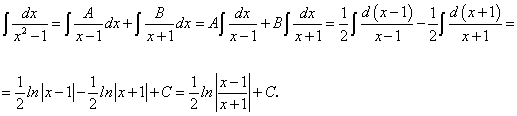
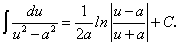
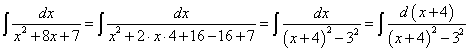 .
.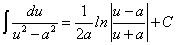 .
.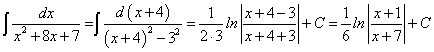 .
.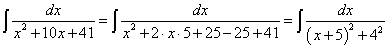 .
.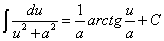 .
.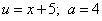 . Имеем:
. Имеем: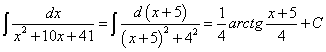 .
.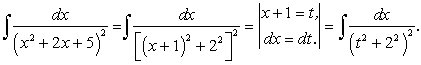
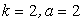 , имеем:
, имеем: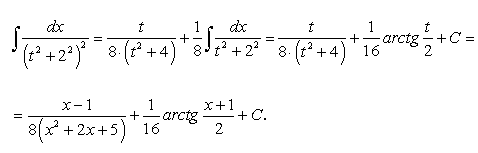
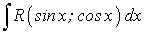 , (188)
, (188)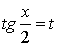 . (189)
. (189)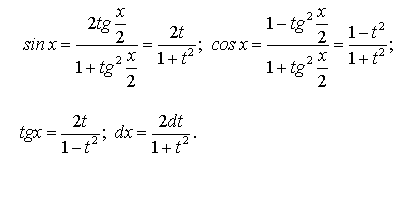 (190)
(190) (191)
(191)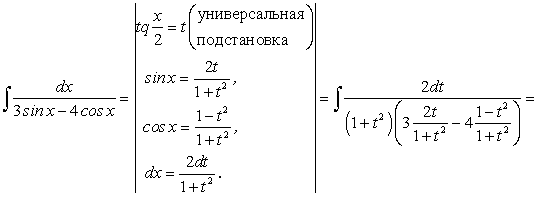
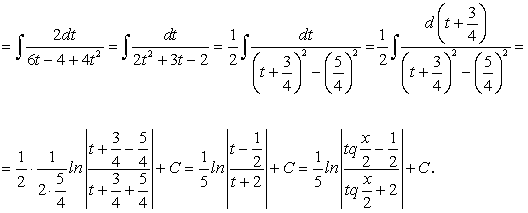
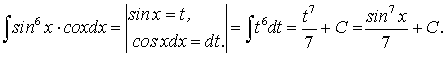
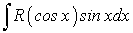 .
.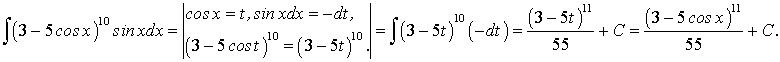
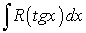 .
.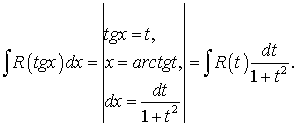
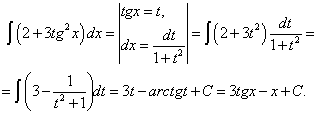
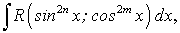
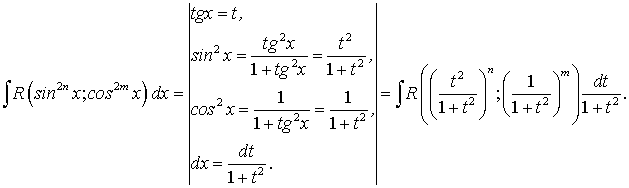
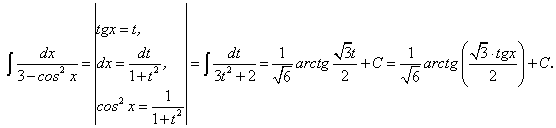
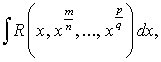
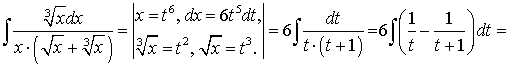
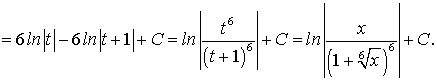
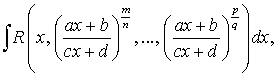
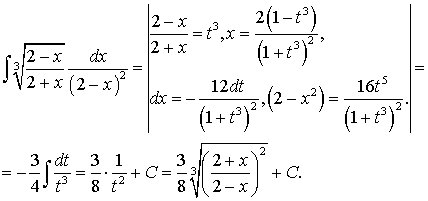
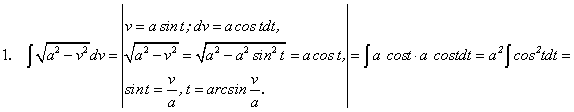
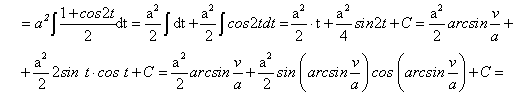
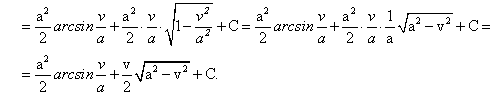
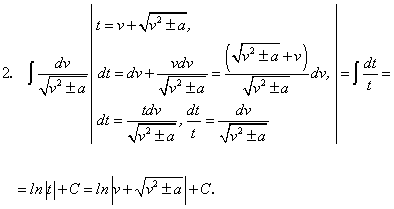
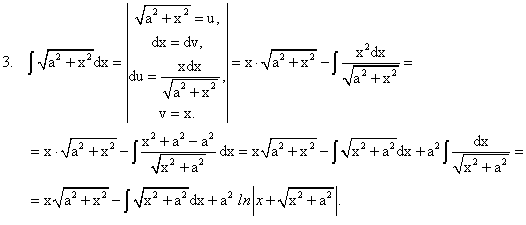
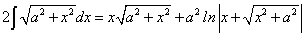 , или
, или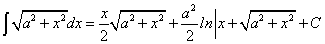 .
.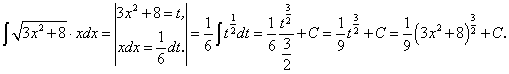
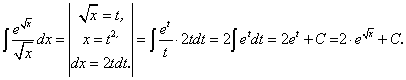
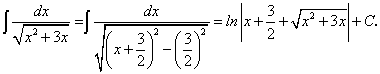
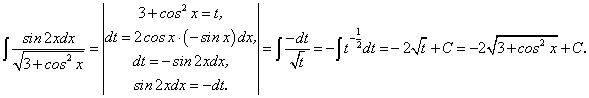
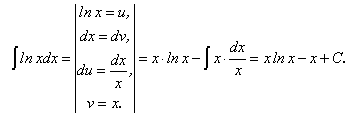
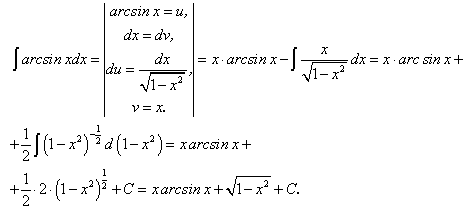
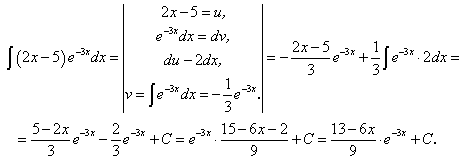
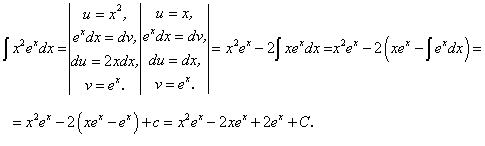
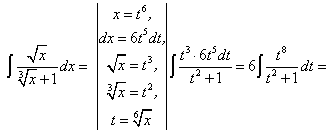
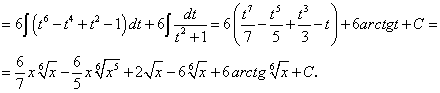
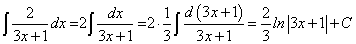 .
.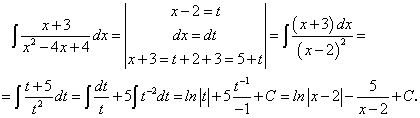
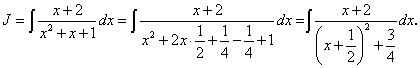
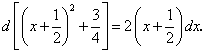
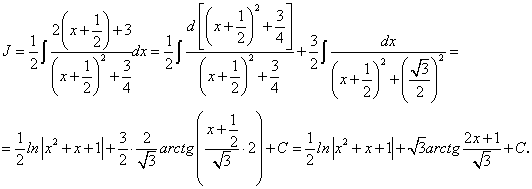
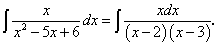
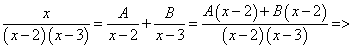
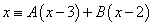 .
.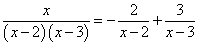 .
.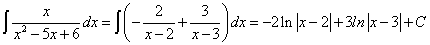 .
.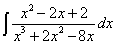 .
.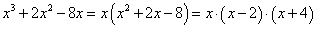 .
.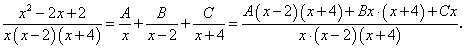
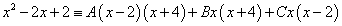 .
.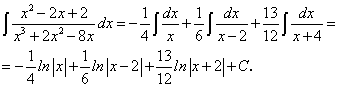
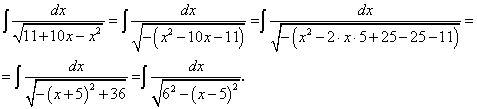
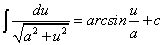 .
.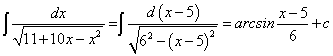 .
.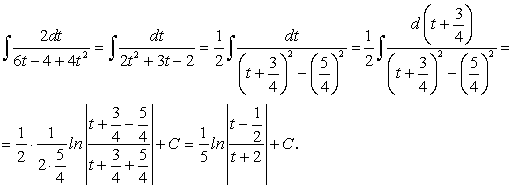
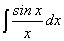 ,
, 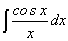 ,
, 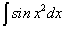 ,
, 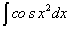 ,
, 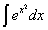
 ;
;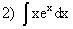 ;
;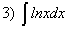 ;
;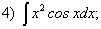
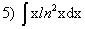 ;
;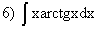 ;
;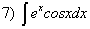 ;
;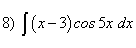 ;
;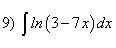 ;
;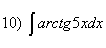 ;
;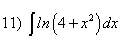 ;
;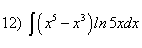 .
.