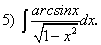Сегодня вы изучите вопросы
-
Неопределенный интеграл
-
Основные свойства неопределенных интегралов
-
Геометрический смысл неопределенного интеграла
-
Таблица простейших неопределенных интегралов
-
Методы интегрирования неопределенного интеграла
Изучив тему занятия, вы сможете
-
по таблице неопределенных интегралов найти первообразные;
-
используя методы интегрирования найти нетабличные интегралы.
Основные понятия
В предыдущем разделе по заданной функции 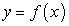 по известным формулам была найдена ее производная. Например, если
по известным формулам была найдена ее производная. Например, если 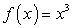 , то по формуле отыскания производной степенной функции
, то по формуле отыскания производной степенной функции 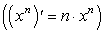 находим, что
находим, что 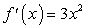 .
.
Пусть требуется решить обратную задачу: дана функция, являющаяся производной некоторой функции; требуется найти такую функцию, первая производная которой равна заданной функции.
Например, пусть 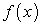 — производная некоторой функции. Обратная задача состоит в отыскании такой функции
— производная некоторой функции. Обратная задача состоит в отыскании такой функции 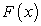 , для которой
, для которой 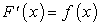 .
.
Функция 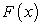 называется первообразной
называется первообразной для функции
для функции 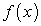 .
.
Таким образом, по определению первообразной, если 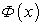 — первообразная функции
— первообразная функции 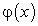 , то
, то 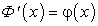 .
.
Покажем, что если функция имеет первообразную, то она их имеет бесчисленное множество. А именно, если 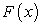 — первообразная функции
— первообразная функции 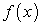 , то
, то 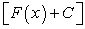 , где С — произвольная постоянная, также является первообразной функции
, где С — произвольная постоянная, также является первообразной функции 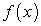 .
.
Действительно:
Докажем следующее утверждение. Если 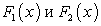 — две произвольные первообразные функции
— две произвольные первообразные функции 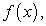 то
то 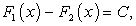 где С — произвольная постоянная.
где С — произвольная постоянная.
Действительно, по условию 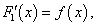
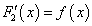 . Отсюда находим:
. Отсюда находим:
Последнее равенство возможно лишь в том случае, когда 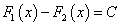 , где С — произвольная постоянная, ч.т.д.
, где С — произвольная постоянная, ч.т.д.
Совокупность (множество) всех первообразных заданной функции 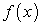 называется неопределенным интегралом
называется неопределенным интегралом этой функции и символически обозначается так:
этой функции и символически обозначается так:
Таким образом, если 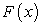 — первообразная функции
— первообразная функции 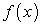 и С — произвольная постоянная, то по определению неопределенного интеграла:
и С — произвольная постоянная, то по определению неопределенного интеграла:
Здесь 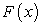 — некоторая первообразная функция для функции
— некоторая первообразная функция для функции 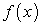 , С — произвольная постоянная.
, С — произвольная постоянная.
Для проверки правильности равенства (155) необходимо проверить справедливость равенства:
Например, пусть дано равенство:
Требуется проверить справедливость равенства (157).
Находим: 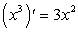 . Подынтегральная функция заданного интеграла равна x2, а не 3x2.
. Подынтегральная функция заданного интеграла равна x2, а не 3x2.
Вывод: равенство (157) является неверным, т.е. 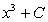 не является совокупностью всех первообразных функции
не является совокупностью всех первообразных функции 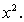 Заметим, что
Заметим, что 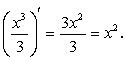 Отсюда следует, что
Отсюда следует, что 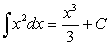 .
.
Процесс отыскания первообразной заданной функции 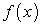 называют интегрированием неопределенного интеграла
называют интегрированием неопределенного интеграла .
.
Задача интегрирования неопределенного интеграла («взять интеграл») заключается в следующем: по заданной функции 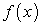 требуется найти такую функцию
требуется найти такую функцию 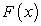 , чтобы
, чтобы 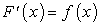 .
.
В учебнике [1] (теорема существования неопределенного интеграла) доказывается, что, если функция 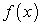 непрерывна, то первообразная функций
непрерывна, то первообразная функций 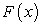 всегда существует.
всегда существует.
Естественно, теорема существования неопределенного интеграла не указывает пути отыскания первообразных, она лишь констатирует факт его существования. Поэтому отыскание первообразных заданных функций требует определенных навыков и умений.
Принцип отыскания неопределенных интегралов очень схож с известным принципом решения множества других задач: вначале решаются простейшие задачи, находятся их решения, а решение более сложных задач стараются перевести в известные простейшие. Заметим, так мы поступали при решении степенных, логарифмических, показательных и тригонометрических уравнений.
Так мы поступим и сейчас: мы вначале найдем первообразные от простейших функций (имеется в виду, что первообразные этих функций почти очевидны), а затем перейдем к отысканию первообразных более сложных функций.
Предварительно изучим основные свойства неопределенных интегралов.
-
Производная от неопределенного интеграла равна подынтегральной функции, т.е.
-
Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
Действительно:
-
Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е.
Действительно,
-
Постоянный множитель подынтегральной функции можно выносить за знак неопределенного интеграла, т.е.
Заметим, что равенство неопределенных интегралов понимается с точностью до произвольно постоянной величины.
где
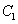 и
и 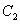 — произвольных постоянные.
— произвольных постоянные.где
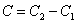 , т.е. функции отличаются на произвольную константу. Поэтому достаточно доказать равенство дифференциалов (или производных) от каждой части равенства:
, т.е. функции отличаются на произвольную константу. Поэтому достаточно доказать равенство дифференциалов (или производных) от каждой части равенства: -
Неопределенный интеграл от алгебраической суммы конечного числа интегрируемых функций равен алгебраической сумме неопределенных интегралов от слагаемых функций, т.е.:
Действительно,
Пусть существует неопределенный интеграл 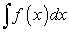 , который по определению равен некоторой функции
, который по определению равен некоторой функции 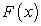 плюс произвольная постоянная С, т.е.
плюс произвольная постоянная С, т.е. 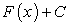 .
.
Геометрически графиком функции 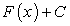 будет семейство линий, полученных из графика функции
будет семейство линий, полученных из графика функции 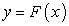 смещением вдоль оси Оу на величину С. Придавая С произвольные значения, получим семейство интегральных линий.
смещением вдоль оси Оу на величину С. Придавая С произвольные значения, получим семейство интегральных линий.
Заметим, что в каждой точке этих линий 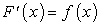 , т.е. угловой коэффициент касательной в точке линии равен значению функции
, т.е. угловой коэффициент касательной в точке линии равен значению функции 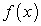 .
.
В частности, 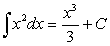 представляет семейство линий (кубических парабол), изображенных на рис. 4.1
представляет семейство линий (кубических парабол), изображенных на рис. 4.1 .
.
Из определения неопределенного интеграла следует, что достаточно взять производную произвольно взятой функции, чтобы найти ее первообразную.
Следовательно,
Этим мы воспользуемся при составлении таблицы простейших неопределенных интегралов. В частности, найдем производную дроби 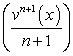 :
:
Отсюда:
или
Заметим, что равенство дифференциалов двух функций, так же как и равенство производных, означает, что эти функции отличаются друг от друга на произвольную постоянную величину.
Найдем:
Отсюда, в частности:
Далее:
Аналогично получим:
Рассмотрим интеграл:
По аналогии находим:
В дальнейшем для краткости записи формул функцию 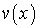 мы будем обозначать через
мы будем обозначать через 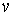 .
.
Рассмотрим интеграл:
Воспользуемся равенством (168) и формулами приведения тригонометрических функций при нахождении следующего интеграла:
Найдем интеграл, подынтегральная функция которого равна обратной величине разности квадратов переменной интегрирования и постоянной величины:
Интегралы от следующих функций найдены на основе таблицы производных:
Рассмотрим интеграл:
В справедливости равенства 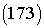 можно убедиться непосредственной проверкой, то есть дифференцированием:
можно убедиться непосредственной проверкой, то есть дифференцированием:
Проверку справедливости нижеприведенных равенств предоставляем читателю:
Интегралы от функций 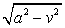 ,
, 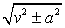 находятся с помощью особых способов, которые будут приведены в следующих пунктах настоящего занятия.
находятся с помощью особых способов, которые будут приведены в следующих пунктах настоящего занятия.
Таким образом, нами получена следующая основная простейшая таблица неопределенных интегралов, куда включены и ряд свойств неопределенных интегралов. Переменная интегрирования преднамеренно нами обозначена через 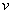 . Это обозначение предусматривает следующую цель: под
. Это обозначение предусматривает следующую цель: под 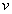 можно понимать любое выражение.
можно понимать любое выражение.
Например, по таблице интегралов, 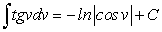 .
.
Таблица интегралов 1. 12. 2. 13. 3. 14. 4. 15. 5. 16. 6. 17. 7. 18. 8. 19. 9. 20. 10. 21. 11 .
![]()
![]()
![]()
![]()
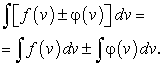
![]()
![]()
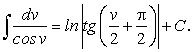
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
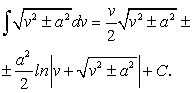
![]() .
. 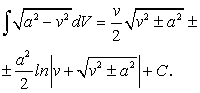
![]()
-
Метод непосредственного интегрирования
 .
.Этот метод заключается в сведении заданного интеграла к табличному путем простейших преобразований с применением основных свойств неопределенных интегралов.
Проиллюстрируем этот метод на примерах.
Примеры:
-
Метод замены переменной интегрирования
 .
.Пусть требуется найти интеграл
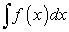 , где подынтегральная функция
, где подынтегральная функция 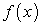 подразумевается непрерывной, а значит, неопределенный интеграл от нее существует, и пусть заданный интеграл не поддается непосредственному интегрированию. Однако если переменную х интегрирования заменить функцией новой переменной
подразумевается непрерывной, а значит, неопределенный интеграл от нее существует, и пусть заданный интеграл не поддается непосредственному интегрированию. Однако если переменную х интегрирования заменить функцией новой переменной 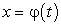 , то получим интеграл от переменной t, который можно свести к табличному интегралу. После интеграции по переменной t необходимо вернуться к прежней переменной х. Этим и завершается метод замены переменной.
, то получим интеграл от переменной t, который можно свести к табличному интегралу. После интеграции по переменной t необходимо вернуться к прежней переменной х. Этим и завершается метод замены переменной.Формально это выглядит так:
Для справедливости вышеприведенного равенства необходимы следующие условия:
В справедливости равенства можно убедиться путем доказательства равенств производных по х от обеих частей, поскольку подобные равенства нами понимаются с точностью до произвольных постоянных величин:
Примеры:
-
Пусть требуется найти неопределенный интеграл
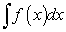 от непрерывной функции
от непрерывной функции 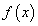 , при этом заданный интеграл не поддается интегрированию известными нам методами. Однако если некоторое выражение от х в подынтегральной функции
, при этом заданный интеграл не поддается интегрированию известными нам методами. Однако если некоторое выражение от х в подынтегральной функции 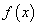 обозначить через новую переменную t, то получим интеграл, который сводится к табличному.
обозначить через новую переменную t, то получим интеграл, который сводится к табличному.Этот метод интегрирования называется способом подстановки. Формально этот метод выглядит так:
Докажем справедливость равенства (176):
Требования, предъявляемые к функциям, аналогичны: функция
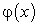 должна быть дифференцируема, иметь обратную функцию, функция
должна быть дифференцируема, иметь обратную функцию, функция 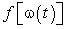 существует и непрерывна.
существует и непрерывна.Примеры:
Приведенные интегралы можно было бы раскрыть и без применения способа подстановки, если воспользоваться таблицей дифференциалов основных элементарных функций.
Такой способ подстановки получил название подведения под знак дифференциала.
Контрольные вопросы
-
Что называется первообразной заданной функции f(х)?
-
Что называется неопределенным интегралом функции f(х)?
-
Сформулируйте и докажите основные свойства неопределенных интегралов.
-
Напишите формулу замены переменной в неопределенном интеграле.
-
Напишите формулу подстановки в неопределенном интеграле.
-
Напишите на память таблицу неопределенных интегралов и сверьте вашу таблицу c таблицей в пособии. Добейтесь полного их совпадения, после чего рекомендуем приступать к отысканию неопределенных интегралов.
Задания для самостоятельной работы
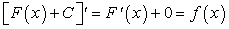 ,
,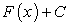 первообразная функции
первообразная функции 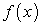 .
.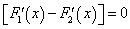 , или
, или 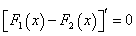 .
.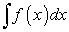 ,
,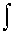 — знак интеграла;
— знак интеграла;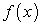 — подынтегральная функция;
— подынтегральная функция;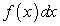 — подынтегральное выражение;
— подынтегральное выражение;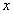 — переменная интегрирования.
— переменная интегрирования.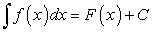 . (155)
. (155)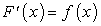 . (156)
. (156)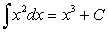 . (157)
. (157)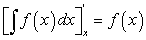 .
.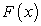 — первообразная
— первообразная 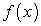 . Тогда:
. Тогда: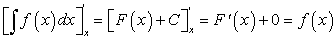 .
.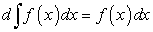 .
.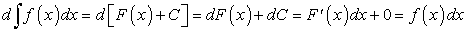 .
.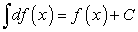 .
.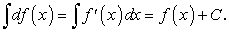
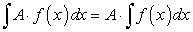 ,
,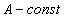 .
.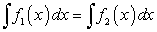 , то
, то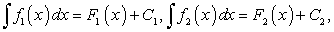
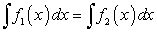 следует, что:
следует, что: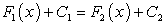 ,
, 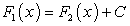 ,
,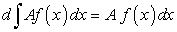 ;
;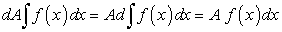 .
.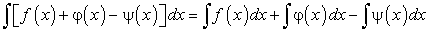 .
.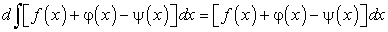 ;
;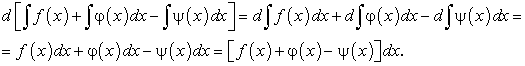
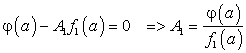 . Отсюда:
. Отсюда: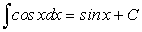 .
.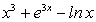 :
: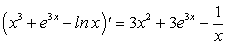 .
.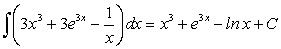 .
.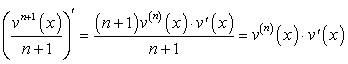 .
.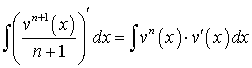 ,
,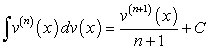 . (158)
. (158)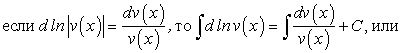
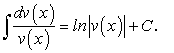 (159)
(159)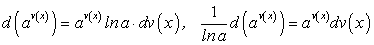 .
.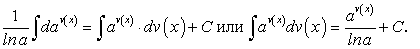 (160)
(160)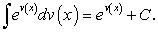 (161)
(161)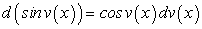 .
.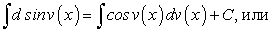
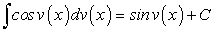 . (162)
. (162)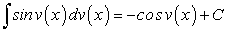 , (163)
, (163)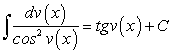 , (164)
, (164)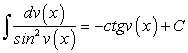 . (165)
. (165)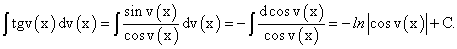 (166)
(166)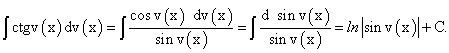 (167)
(167)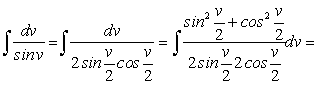 (168)
(168)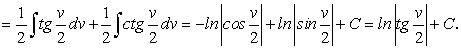
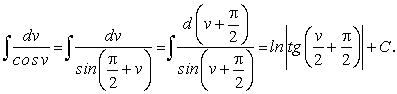 (169)
(169)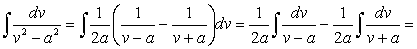
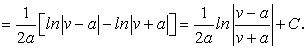 (170)
(170)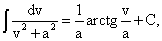 т.к.
т.к.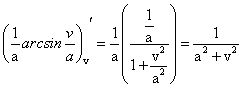 (171)
(171)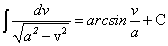 ,т.к.
,т.к.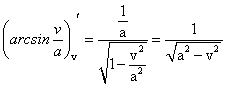 (172)
(172)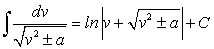 . (173)
. (173)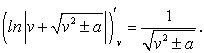
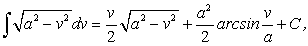 (174)
(174)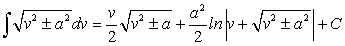 . (175)
. (175)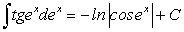 .
.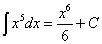 .
.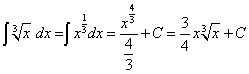 .
.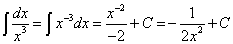 .
.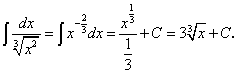
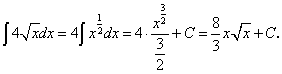
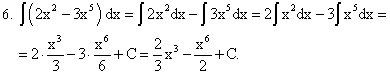
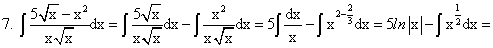
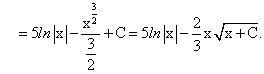
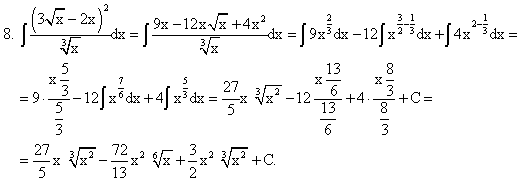
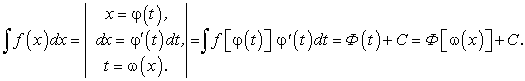
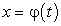 дифференцируема;
дифференцируема;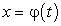 имеет обратную функцию;
имеет обратную функцию;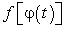 существует и непрерывна.
существует и непрерывна.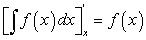 ;
;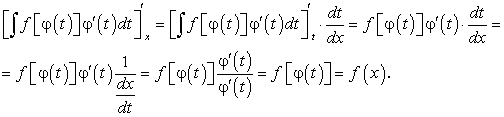
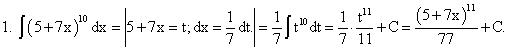
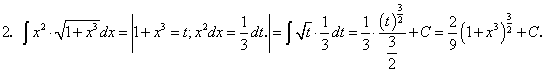
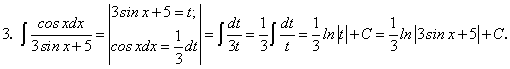
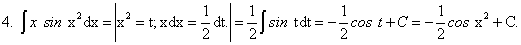
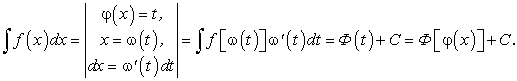 (176)
(176)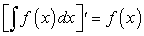 ,
,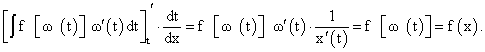
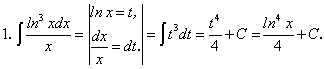
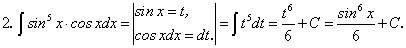
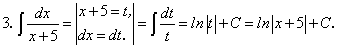
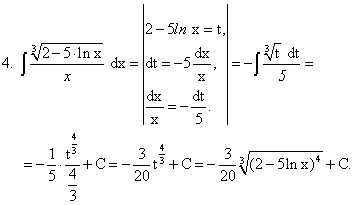
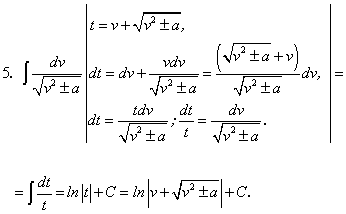
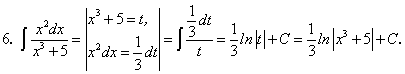
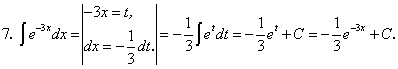
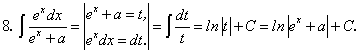
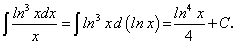
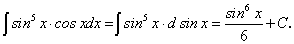
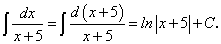
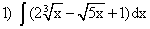 ;
;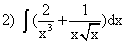 ;
;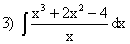 ;
;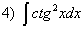 ;
;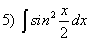 ;
;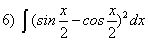 ;
;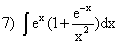 ;
;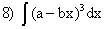 ;
;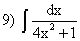 ;
;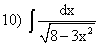 ;
;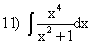 ;
;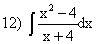 ;
;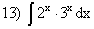 ;
;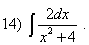
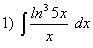 ;
;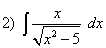 ;
;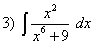 ;
;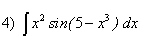 ;
;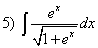 ;
;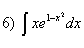 ;
;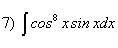 ;
;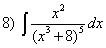 ;
;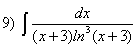 ;
;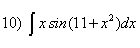 ;
;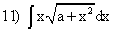 ;
;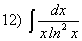 ;
;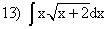 (подстановка
(подстановка 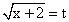 );
);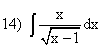 ;
;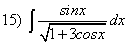 (подстановка
(подстановка 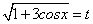 ).
).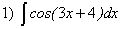 ;
;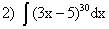 ;
;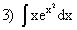 ;
;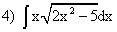 ;
;