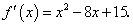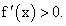Сегодня вы изучите вопросы
-
Основные теоремы дифференцируемых функций
-
Первая теорема Лопиталя
-
Вторая теорема Лопиталя
-
Исследование функций. Возрастание и убывание функции
Изучив тему занятия, вы сможете
-
раскрыть неопределенности по правилам Лопиталя;
-
найти область монотонного возрастания и убывания функции.
Основные понятия
Рассмотрим непрерывную функцию на отрезке 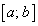 , график которой представлен гладкой линией, т.е. в каждой точке этой линии существует единственная касательная. Пусть эта функция принимает одинаковые значения на концах этого отрезка:
, график которой представлен гладкой линией, т.е. в каждой точке этой линии существует единственная касательная. Пусть эта функция принимает одинаковые значения на концах этого отрезка: 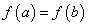 (рис. 3.1
(рис. 3.1 ).
).
Исследование функции опирается на ряд фундаментальных теорем математического анализа, с которых мы и начнем настоящее занятие.
Следующей теоремой утверждается, что на интервале (a; b) найдется хотя бы одна точка, касательная в которой параллельна оси Ox.
Теорема Ролля . Если функция
. Если функция 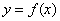 непрерывна на отрезке
непрерывна на отрезке 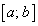 , дифференцируема во всех ее внутренних точках и значения функции на концах равны, т.е.
, дифференцируема во всех ее внутренних точках и значения функции на концах равны, т.е. 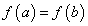 , то внутри отрезка
, то внутри отрезка 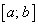 найдется по крайней мере одна такая точка
найдется по крайней мере одна такая точка 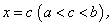 что
что 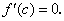
Доказательство теоремы Ролля можно найти в учебнике по математическому анализу [1].
Следует отметить, что каждое условие теоремы Ролля является необходимым. Например, если 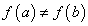 , то для отрезка прямой АВ (рис. 3.2
, то для отрезка прямой АВ (рис. 3.2 ) могут выполняться все остальные условия теоремы Ролля, но, тем не менее, на отрезке АВ не существует ни одной точки, касательная в которой параллельна оси
) могут выполняться все остальные условия теоремы Ролля, но, тем не менее, на отрезке АВ не существует ни одной точки, касательная в которой параллельна оси  , так как в любой ее внутренней точке
, так как в любой ее внутренней точке 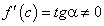 .
.
Если функция 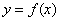 на концах отрезка имеет равные значения, а внутри отрезка
на концах отрезка имеет равные значения, а внутри отрезка 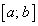 найдется хотя бы одна точка, производная в которой не существует, то утверждение теоремы может быть неверным.
найдется хотя бы одна точка, производная в которой не существует, то утверждение теоремы может быть неверным.
Действительно, функция 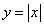 на отрезке [-1; 1] имеет точку
на отрезке [-1; 1] имеет точку 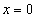 , в которой нет производной. Как легко заметить (см. рис. 3.3
, в которой нет производной. Как легко заметить (см. рис. 3.3 ), нет ни одной внутренней точки отрезка [-1; 1], где бы производная равнялась нулю.
), нет ни одной внутренней точки отрезка [-1; 1], где бы производная равнялась нулю.
На основе следующей теоремы, опирающейся на теорему Ролля, доказываются все утверждения, связанные с исследованием функции: отыскание интервалов монотонного возрастания и убывания, отыскание максимумов и минимумов функции, интервалов выпуклости и вогнутости и т.д.
Теорема Лагранжа (теорема о конечных приращениях). Если функция
(теорема о конечных приращениях). Если функция 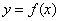 непрерывна на отрезке
непрерывна на отрезке 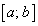 и дифференцируема во всех ее внутренних точках, то внутри отрезка
и дифференцируема во всех ее внутренних точках, то внутри отрезка 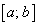 найдется по крайней мере одна такая точка
найдется по крайней мере одна такая точка 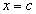
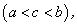 что:
что:
Для доказательства построим вспомогательную функцию 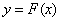 , которая бы удовлетворяла условиям теоремы Ролля:
, которая бы удовлетворяла условиям теоремы Ролля:
Построенная нами функция 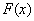 удовлетворяет всем условиям теоремы Ролля: она непрерывна на отрезке
удовлетворяет всем условиям теоремы Ролля: она непрерывна на отрезке 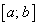 и дифференцируема во всех ее внутренних точках, так как таковыми являются функции, из которых она состоит. Остается проверить равенство значений этой функции на концах отрезка
и дифференцируема во всех ее внутренних точках, так как таковыми являются функции, из которых она состоит. Остается проверить равенство значений этой функции на концах отрезка 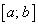 :
:
Следовательно, по теореме Ролля, внутри отрезка 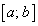 найдется по крайней мере одна такая точка
найдется по крайней мере одна такая точка 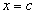
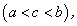 что
что 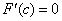 .
.
Подставив вместо 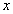 значение
значение 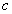 , находим:
, находим:
Отсюда окончательно находим, что 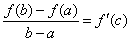 , ч.т.д.
, ч.т.д.
Теорема Лагранжа имеет простое геометрическое толкование: если в прямоугольной декартовой системе координат задана на интервале 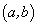 гладкая линия, непрерывная на концах этого интервала (что означает существование односторонних пределов
гладкая линия, непрерывная на концах этого интервала (что означает существование односторонних пределов 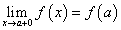 ,
, 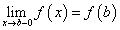 ), то внутри интервала
), то внутри интервала 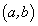 непременно найдется такая точка
непременно найдется такая точка 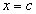 , касательная в которой параллельна хорде АВ, соединяющей концы отрезка
, касательная в которой параллельна хорде АВ, соединяющей концы отрезка 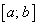 (рис. 3.4
(рис. 3.4 ).
).
Равенство (126) называется формулой Лагранжа , или формулой конечных приращений
, или формулой конечных приращений .
.
Формула Лагранжа имеет различные формы записи. Например,
Далее, так как 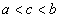 , то
, то 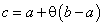 , где
, где 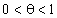 , то формулу Лагранжа можно переписать так:
, то формулу Лагранжа можно переписать так:
Если в (128) за 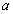 принять
принять 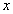 , а за
, а за 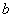 принять
принять 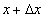 , то
, то 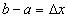 и формула Лагранжа (127) перепишется так:
и формула Лагранжа (127) перепишется так:
Обобщением теоремы Лагранжа является теорема О.Л. Коши .
.
Теорема 18 (теорема Коши). Если функции 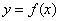 и
и 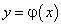 непрерывны на отрезке
непрерывны на отрезке 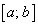 и дифференцируемы во всех ее внутренних точках, причем
и дифференцируемы во всех ее внутренних точках, причем 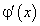 не равно нулю ни в одной внутренней точке отрезка
не равно нулю ни в одной внутренней точке отрезка 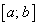 , то внутри отрезка
, то внутри отрезка 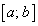 найдется по крайней мере одна такая точка
найдется по крайней мере одна такая точка 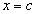
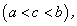 что:
что:
Доказательство теоремы Коши можно найти в учебнике [1]. Из формулы Коши (131) легко получить формулу Лагранжа, если положить 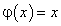 . Действительно, из равенства (131) имеем:
. Действительно, из равенства (131) имеем:
Теорема Коши имеет простое геометрическое толкование, как и теорема Лагранжа: на гладкой линии, заданной на отрезке 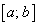 , всегда найдется по крайней мере одна такая точка, касательная в которой параллельна хорде, соединяющей концы гладкой линии. Отличие заключается в том, что в теореме Коши гладкая линия задана параметрическими уравнениями
, всегда найдется по крайней мере одна такая точка, касательная в которой параллельна хорде, соединяющей концы гладкой линии. Отличие заключается в том, что в теореме Коши гладкая линия задана параметрическими уравнениями
По условиям теоремы Коши функции 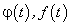 удовлетворяют всем условиям существования производной функции, заданной параметрически.
удовлетворяют всем условиям существования производной функции, заданной параметрически.
Пусть С — произвольная внутренняя точка графика функции (рис. 3.5 ), которой соответствует значение параметра
), которой соответствует значение параметра 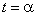 , где
, где 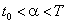 и
и 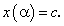
Найдем угловой коэффициент касательной в точке С:
Угловой коэффициент прямой, проходящей через точки А и В, равен:
По теореме Коши справедливо равенство
Отсюда окончательно находим, что угловые коэффициенты хорды и касательной равны: 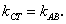
При вычислении пределов 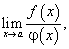 когда
когда 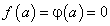 , для раскрытия неопределенностей вида
, для раскрытия неопределенностей вида 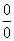 мы сталкивались с определенными трудностями. В некоторых случаях при переходе от предела отношения функций к пределу отношения их производных значительно упрощается отыскание указанных пределов.
мы сталкивались с определенными трудностями. В некоторых случаях при переходе от предела отношения функций к пределу отношения их производных значительно упрощается отыскание указанных пределов.
Первая теорема Лопиталя указывает, когда такой переход правомочен.
Формулировка теоремы.
Если:
1) функции 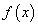 и
и 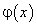 непрерывны на отрезке
непрерывны на отрезке 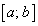 и
и 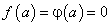 ,
,
2) функции 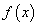 и
и 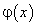 дифференцируемы на интервале
дифференцируемы на интервале 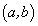 , причем
, причем 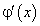 не обращается в нуль ни в одной точке этого интервала,
не обращается в нуль ни в одной точке этого интервала,
то при сформулированных условиях существует предел 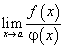 , причем:
, причем:
Доказательство. По теореме Коши имеем:
Из равенств (133) имеем:
Таким образом, при сформулированных условиях при раскрытии неопределенностей 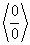 можно от предела отношений функций переходить к пределу отношения их производных.
можно от предела отношений функций переходить к пределу отношения их производных.
Если 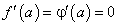 , а функции
, а функции 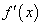 и
и 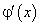 удовлетворяют условиям теоремы Лопиталя, то справедливо равенство:
удовлетворяют условиям теоремы Лопиталя, то справедливо равенство:
В качестве примера рассмотрим предел отношения двух функций, удовлетворяющих условиям первой теоремы Лопиталя:
Если каждый раз при раскрытии неопределенностей мы получаем новые отношения функций, удовлетворяющих условиям теоремы Лопиталя, то предельный переход от отношения функций к пределу отношения их производных можно производить любое конечное число раз.
Если:
1) функции 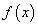 и
и 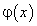 непрерывны на отрезке
непрерывны на отрезке 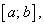
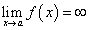
2) функции 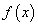 и
и 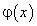 дифференцируемы на интервале
дифференцируемы на интервале 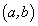 , причем
, причем 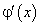 не обращается в нуль ни в одной точке этого интервала,
не обращается в нуль ни в одной точке этого интервала,
тогда при сформулированных условиях существует предел 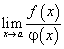 , причем
, причем 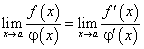 .
.
Из второй теоремы Лопиталя вытекает, что при раскрытии неопределенностей 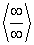 можно при выполнении условий второй теоремы Лопиталя переходить от предела отношения функций к пределу отношения их производных, а при выполнении условий теоремы для отношения первых производных числителя и знаменателя можно переходить к пределу отношения их вторых производных и т.д.
можно при выполнении условий второй теоремы Лопиталя переходить от предела отношения функций к пределу отношения их производных, а при выполнении условий теоремы для отношения первых производных числителя и знаменателя можно переходить к пределу отношения их вторых производных и т.д.
Неопределенности вида 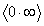 легко сводятся к неопределенностям
легко сводятся к неопределенностям 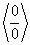 или
или 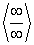 простейшими преобразованиями:
простейшими преобразованиями:
Другие неопределенности вида 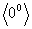 ,
, 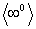 ,
, 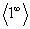 сводятся к неопределенности
сводятся к неопределенности 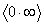 логарифмированием.
логарифмированием.
Например, рассмотрим функцию 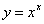 : пусть требуется найти значение этой функции при
: пусть требуется найти значение этой функции при 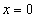 . Отыскание частного значения рассматриваемой функции приводит к раскрытию неопределенности
. Отыскание частного значения рассматриваемой функции приводит к раскрытию неопределенности 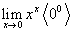 .
.
Возьмем от обеих частей равенства 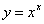 натуральный логарифм:
натуральный логарифм:
Воспользуемся второй теоремой Лопиталя для вычисления неопределенности
Отсюда находим, что:
На первом занятии были даны определения монотонно возрастающих и монотонно убывающих функций Напомним, что функция 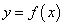 называется монотонно возрастающей во внутренней точке
называется монотонно возрастающей во внутренней точке 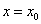 отрезка
отрезка 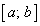 , если для всех точек окрестности
, если для всех точек окрестности 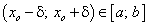 выполняется неравенство
выполняется неравенство 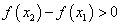 при
при 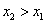 .
.
Следующая теорема с помощью первой производной функции 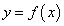 устанавливает интервалы ее монотонного возрастания и убывания.
устанавливает интервалы ее монотонного возрастания и убывания.
Теорема 19. Необходимым и достаточным условием монотонного возрастания (убывания) дифференцируемой функции 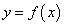 на интервале
на интервале 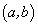 является неравенство
является неравенство 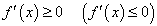 .
.
Доказательство необходимости. Дана функция 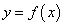 , монотонно возрастающая на интервале
, монотонно возрастающая на интервале 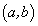 . Требуется доказать, что для произвольной точки
. Требуется доказать, что для произвольной точки 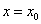 интервала
интервала 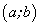 будет выполняться неравенство
будет выполняться неравенство 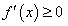 .
.
По определению монотонного возрастания функции в точке для произвольных точек 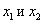 интервала
интервала 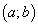 при
при 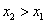 выполняется неравенство
выполняется неравенство 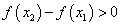 . Если разности
. Если разности 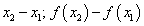 обозначить соответственно через
обозначить соответственно через 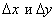 , то отношение
, то отношение 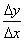 будет всегда положительным, т.к. знаки числителя и знаменателя этой дроби всегда совпадают.
будет всегда положительным, т.к. знаки числителя и знаменателя этой дроби всегда совпадают.
Отсюда следует, что 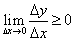 или
или 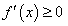 . Здесь следует заметить следующую деталь: при предельном переходе в выражении строгого неравенства всегда возможно равенство. Действительно, при любых значениях
. Здесь следует заметить следующую деталь: при предельном переходе в выражении строгого неравенства всегда возможно равенство. Действительно, при любых значениях 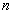 дробь
дробь 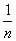 всегда положительна. Однако
всегда положительна. Однако 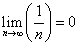 .
.
Таким образом, нами доказана первая часть теоремы.
Докажем ее вторую часть. Дано, что для произвольной точки интервала 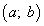 выполняется неравенство
выполняется неравенство 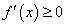 . Требуется доказать, что для произвольных точек
. Требуется доказать, что для произвольных точек 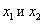 этого интервала при
этого интервала при 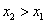 выполняется неравенство
выполняется неравенство 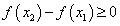 .
.
Для доказательства к разности 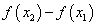 применим формулу Лагранжа (это возможно, так как заданная функция
применим формулу Лагранжа (это возможно, так как заданная функция 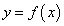 удовлетворяет всем ее условиям):
удовлетворяет всем ее условиям):
где т. 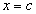 является внутренней точкой интервала
является внутренней точкой интервала 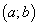 .
.
Так как по условию первая производная 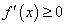 положительна во всех внутренних точках интервала
положительна во всех внутренних точках интервала 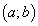 , то она, в частности, положительна и в точке
, то она, в частности, положительна и в точке 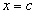 :
: 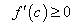 .
.
Далее, так как 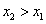 , то
, то 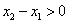 . Отсюда следует, что правая часть равенства (134) неотрицательна, т.е.
. Отсюда следует, что правая часть равенства (134) неотрицательна, т.е. 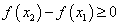 , ч.т.д.
, ч.т.д.
Доказанная теорема имеет простое геометрическое толкование: касательная к графику монотонно возрастающей функции, представленной гладкой линией в прямоугольной системе координат, образует с осью 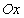 острые углы (рис. 3.6
острые углы (рис. 3.6 ), а в случае монотонного убывания — тупые углы, за исключением некоторых точек, где она параллельна оси
), а в случае монотонного убывания — тупые углы, за исключением некоторых точек, где она параллельна оси 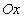 (рис. 3.7
(рис. 3.7 ).
).
Если во всех точках множества Х функция 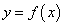 монотонно возрастает или монотонно убывает, то это множество называется для заданной функции множеством монотонного возрастания
монотонно возрастает или монотонно убывает, то это множество называется для заданной функции множеством монотонного возрастания или убывания
или убывания .
.
Так как для произвольной дифференцируемой функции 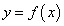 в области ее определения возможны варианты
в области ее определения возможны варианты 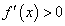 ,
, 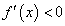 ,
, 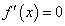 (или
(или 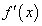 не существует, если функция является кусочно-гладкой), то область определения функции можно разделить на подмножества, где заданная функция либо монотонно возрастает, либо монотонно убывает. Точки, разделяющие эти множества, таковы, что в этих точках первая производная либо равна нулю, либо не существует, либо равна бесконечности.
не существует, если функция является кусочно-гладкой), то область определения функции можно разделить на подмножества, где заданная функция либо монотонно возрастает, либо монотонно убывает. Точки, разделяющие эти множества, таковы, что в этих точках первая производная либо равна нулю, либо не существует, либо равна бесконечности.
Точки, в которых первая производная функции равна нулю, называются стационарными , а точки, в которых первая производная функции не существует или равна бесконечности, называются критическими
, а точки, в которых первая производная функции не существует или равна бесконечности, называются критическими . К критическим точкам иногда причисляют и стационарные точки.
. К критическим точкам иногда причисляют и стационарные точки.
На основании доказанных теорем и сделанных замечаний можно предложить следующий алгоритм исследования функций на возрастание и убывание.
-
Находим критические точки заданной функции, т.е. те точки, где первая производная заданной функции равна нулю, не существует или равна бесконечности.
-
Разбиваем область определения заданной функции на интервалы критическими точками. Исследуем знак первой производной функции на каждом из полученных интервалов. Для этого достаточно внутри каждого интервала взять по произвольной точке и определить знак первой производной в этой точке.
Если в исследуемой точке первая производная больше нуля, то на исследуемом интервале функция монотонно возрастает, если первая производная меньше нуля, то заданная функция монотонно убывает.
Пример 1. Найти интервалы возрастания и убывания функции f(x) = x2 — 3x + 2.
Вывод. При х?(1,5; +?) функция f(x) = x2 — 3x + 2 монотонно возрастает, а в остальной части числовой оси х?(–?; 1,5) — монотонно убывает.
Вывод: функция 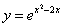 при х ϵ (1; +∞) монотонно возрастет, а в остальных точках числовой оси Oх — х ϵ (–∞; 1) — монотонно убывает.
при х ϵ (1; +∞) монотонно возрастет, а в остальных точках числовой оси Oх — х ϵ (–∞; 1) — монотонно убывает.
Пример 3. Найти промежутки возрастания и убывания функции:
-
Находим первую производную заданной функции:
-
Для этого находим решения уравнения x2 — 8x + 15 = 0:
х1 = 3; х2 = 5.
Числовая ось этими точками делится на части (–∞; 3), (3; 5), (5; +∞).
Исследуем знак первой производной на каждом из этих интервалов.
Для исследования интервала х < 3 или х ϵ (–∞; 3) можно взять значение х = 2:
f'(x)|х = 2 = (х2 — 8х + 15)|х = 2 = 4 — 16 + 15 > 0.
Следовательно, на интервале (–∞; 3) функция монотонно возрастает.
Для исследования интервала (3; 5) можно взять значение х = 4:
f'(x)|х = 4 = 16 — 32 + 15 < 0.
Следовательно, на интервале (3; 5) функция монотонно убывает.
Для исследования интервала (5; +∞) можно взять значение х = 6:
f'(x)|х = 6 = 36 — 48 + 15 > 0.
Следовательно, функция на интервале (5; +∞) монотонно возрастает.
Замечание 1. Если функция имеет точки разрыва на числовой оси, то точки разрыва также нужно включить в число точек, разбивающих область определения функции на интервалы.
Замечание 2. В примере был приведен общий прием отыскания интервалов монотонного возрастания и убывания. В частности, нам известно, что неравенство второй степени х2 — 8х + 15 > 0 имеет решения:
х ϵ (–∞; 3) U (5; +∞),
т.е. заданная функция монотонно возрастает на множестве х ϵ (–∞; 3) U (5; +∞), а на оставшемся множестве (3; 5) — монотонно убывает.
Контрольные вопросы
-
При каких условиях, налагаемых на функцию
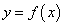 , имеет место теорема Ролля?
, имеет место теорема Ролля? -
При каких условиях, налагаемых на функцию
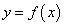 , имеют место теоремы Лагранжа и Коши?
, имеют место теоремы Лагранжа и Коши? -
Можно ли из полученных формул, являющихся результатами теорем Лагранжа и Коши, сформулировать основные требования, налагаемые на функцию
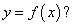 Если да, то обоснуйте утверждение.
Если да, то обоснуйте утверждение. -
Сформулируйте условия, налагаемые на функции в теореме Лопиталя. При каких условиях можно переходить к пределу отношений вторых производных числителя и знаменателя дроби?
-
Каковы условия применения правил Лопиталя?
-
Сформулируйте необходимые и достаточные условия монотонного возрастания (убывания) функции на интервале (а; b).
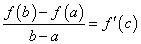 . (126)
. (126)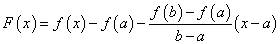 .
.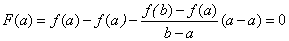 ;
;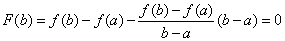 .
.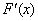 :
: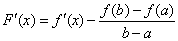 .
.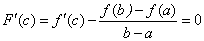 .
.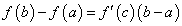 . (127)
. (127)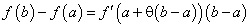 . (128)
. (128)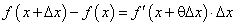 , (129)
, (129)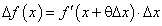 . (130)
. (130)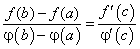 . (131)
. (131)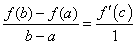 , или
, или 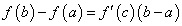 .
.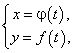 (132)
(132)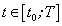 .
.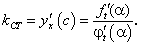
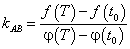 .
.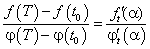 .
.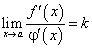 ,
,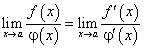 .
.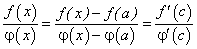 , (133)
, (133)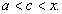
 и
и  .
.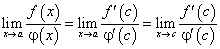 , ч.т.д.
, ч.т.д.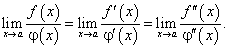 .
.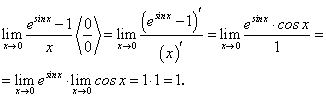
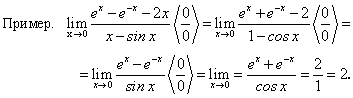
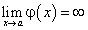 ,
,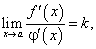
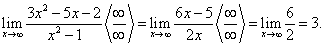
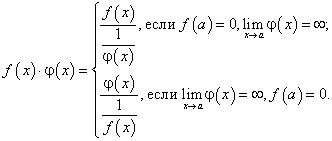
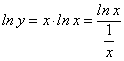 .
.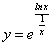 и
и 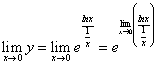 .
.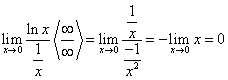 .
.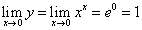 .
.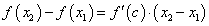 , (134)
, (134) .
.
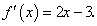
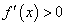 :
: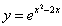 .
. .
.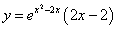
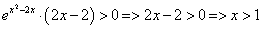 .
.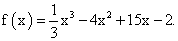
 .
.