Сегодня вы изучите вопросы
-
Предел функции
-
Односторонние пределы функции одной переменной
-
Непрерывность функции
-
Точки разрыва функции
-
Свойства функций, непрерывных на замкнутом интервале
-
Арифметические операции над непрерывными функциями
Изучив тему занятия, вы сможете
-
найти предел функции;
-
определить область непрерывности функции;
-
найти точки разрыва функции.
Основные понятия
Ранее мы изучили предел функции натурального аргумента, то есть функции, независимая переменная которой принимает только целые положительные значения.
В этом разделе раскрывается определение предела функции, когда независимая переменная принимает вещественные значения, и рассматриваются значения функции при стремлении аргумента х к конечному или бесконечному пределу.
Для простоты изложения поясним предел функции с помощью ее графика. Пусть функция 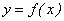 определена в некоторой окрестности точки а числовой оси Ох. Обозначим через b предельное значение функции при х → а. Зададимся наперед заданным числом
определена в некоторой окрестности точки а числовой оси Ох. Обозначим через b предельное значение функции при х → а. Зададимся наперед заданным числом 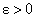 . Проведем прямые, параллельные оси Ох, проходящие через точки b — ε, b + ε, лежащие на оси Оу.
. Проведем прямые, параллельные оси Ох, проходящие через точки b — ε, b + ε, лежащие на оси Оу.
Найдем точки пересечения этих прямых с графиком функции 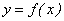 , а также найдем абсциссы этих точек. Обозначим эти абсциссы через x1 и x2 (рис. 1.3
, а также найдем абсциссы этих точек. Обозначим эти абсциссы через x1 и x2 (рис. 1.3 ).
).
Заметим, что для всех х, находящихся внутри интервала (x1, x2), выполняется неравенство:
Возьмем δ-окрестность точки х = а: (а — δ; а + δ), где δ > 0 и меньше, чем |а — х1| и |а — х2|.
Очевидно (рис. 1.3), что для х ϵ (а — δ; а + δ) тем более выполняется неравенство (16).
Отсюда вытекает следующее определение предела функции.
Число b называется пределом функции
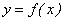 при х → а, если для любого сколь угодно малого наперед заданного положительного числа
при х → а, если для любого сколь угодно малого наперед заданного положительного числа 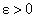 найдется такое число
найдется такое число 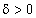 , что для всех x, отличных от a и таких, что |х — а| < δ, будет выполняться неравенство
, что для всех x, отличных от a и таких, что |х — а| < δ, будет выполняться неравенство 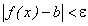 .
.
Символически это записывается так:
Из определения предела функции следует, что, если существует предел (17), то, каково бы ни было 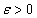 , можно найти такую δ-окрестность точки a, что для всех точек этой окрестности будет выполняться неравенство
, можно найти такую δ-окрестность точки a, что для всех точек этой окрестности будет выполняться неравенство 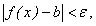 или
или 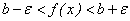 , т.е. значения ординат функции
, т.е. значения ординат функции 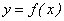 будут находиться в ε-окрестности точки b. Геометрически это означает, что точки графика функции
будут находиться в ε-окрестности точки b. Геометрически это означает, что точки графика функции 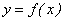 будут находиться в полосе шириной в 2ε, границами которой являются прямые
будут находиться в полосе шириной в 2ε, границами которой являются прямые 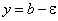 и
и 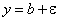 .
.
Из определения предела функции (рис. 1.3) следует, что δ находится в прямой зависимости от 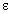 : чем меньше
: чем меньше 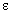 , тем меньше δ. Однако из определения трудно усмотреть зависимость δ от точки
, тем меньше δ. Однако из определения трудно усмотреть зависимость δ от точки 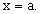
Для наглядности рассмотрим функцию 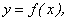 представленную своим графиком (рис. 1.4
представленную своим графиком (рис. 1.4 ).
).
Для всех точек области определения функции зададимся одним и тем же ε > 0.
Для точки х = х1 для удовлетворения условия |f(x)- b1| < ε при х → х1 достаточно взять δ < |B2 x1|, а для удовлетворения условия |f(x) — b2| < ε при х → х2 достаточно взять 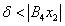 .
.
Сравнивая отрезки |B2 x1| и |B4 x2| (см. рис. 1.4), легко видеть, что 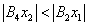 . Таким образом, для одного и того же значения
. Таким образом, для одного и того же значения 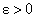 значение δ разное для удовлетворения неравенства (16). Отсюда вытекает, что δ зависит от точки х = а.
значение δ разное для удовлетворения неравенства (16). Отсюда вытекает, что δ зависит от точки х = а.
С односторонними пределами мы познакомились при определении предела последовательности 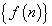 или
или 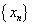 , где
, где 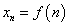 .
.
Аналогично определяются односторонние пределы для функции 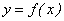 : пределом слева функции
: пределом слева функции 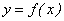 при х → а (обозначается f (a — 0)) называется предел этой функции, когда х принимает действительные значения в области определения функции, не превосходящие значения х = а, т.е. значения х на числовой оси располагаются левее точки х = а; пределом справа функции
при х → а (обозначается f (a — 0)) называется предел этой функции, когда х принимает действительные значения в области определения функции, не превосходящие значения х = а, т.е. значения х на числовой оси располагаются левее точки х = а; пределом справа функции 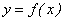 при х → а (обозначается
при х → а (обозначается 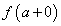 ) называется предел этой функции, когда х принимает действительные значения в области определения функции, превосходящие значения
) называется предел этой функции, когда х принимает действительные значения в области определения функции, превосходящие значения 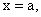 т.е. значения х на числовой оси располагаются правее точки
т.е. значения х на числовой оси располагаются правее точки 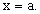
Символически односторонние пределы обозначаются еще так:
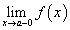 — предел слева,
— предел слева, 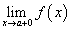 — предел справа.
— предел справа.
В качестве примера для определения односторонних пределов рассмотрим функцию, заданную аналитически:
График заданной функции 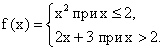 представлен на рис. 1.5
представлен на рис. 1.5 :
:
Найдем односторонние пределы заданной функции:
Отсюда следует, что заданная функция имеет односторонние пределы, которые не равны между собой.
Такая функция называется разрывной. Как следует из графика функции  (рис. 1.5), мы имеем разрыв в точке, абсцисса которой равна 2.
(рис. 1.5), мы имеем разрыв в точке, абсцисса которой равна 2.
Для существования предела функции  в точке х = а необходимо и достаточно, чтобы:
в точке х = а необходимо и достаточно, чтобы:
1) функция f(х) была определена в некоторой окрестности точки х = a;
2) существовали односторонние пределы  ,
, 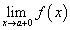 ;
;
3) эти пределы были равны между собой:
Рассмотрим случай, когда аргумент 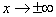 .
.
Число b называется пределом функции
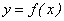 при
при 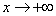 , если для произвольного
, если для произвольного 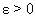 можно найти такое
можно найти такое 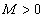 , что для всех значений х, для которых
, что для всех значений х, для которых 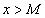 , будет выполняться неравенство
, будет выполняться неравенство 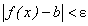 .
.
Символически это записывается так: 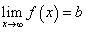 .
.
Аналогично определяется предел функции 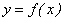 при
при 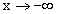 :
:
Число b называется пределом функции 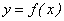 при
при 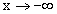 , если для произвольного
, если для произвольного 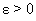 можно найти такое
можно найти такое 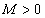 , что для всех значений x, для которых
, что для всех значений x, для которых 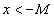 , будет выполняться неравенство
, будет выполняться неравенство 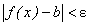 .
.
Символически это записывается так: 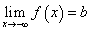 .
.
Поясним данные определения на графике (рис. 1.6 ). На рисунке 1.6 функция y = f(x) при x → +∞ имеет предел, равный b > 0.
). На рисунке 1.6 функция y = f(x) при x → +∞ имеет предел, равный b > 0.
Возьмем ε-окрестность точки (0; b) на оси Оу. Через точки (0, b — ε), (0, b + ε) оси Оу проведем прямые, параллельные оси Ох.
В результате получим полосу шириною в 2ε.
Найдем абсциссу точки пересечения прямой 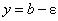 с графиком функции
с графиком функции 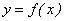 .
.
Обозначим эту абсциссу через М. Заметим, что для всех 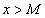 выполняется неравенство
выполняется неравенство 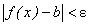 , т.е. точки графика функции, абсциссы которых удовлетворяют неравенству
, т.е. точки графика функции, абсциссы которых удовлетворяют неравенству 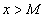 , целиком находятся в вышеуказанной полосе. Это означает, что ординаты функции
, целиком находятся в вышеуказанной полосе. Это означает, что ординаты функции 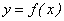 находятся в
находятся в 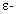 окрестности точки b:
окрестности точки b: 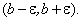
Мы рассмотрели случай, когда 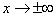 , а предел функции b — число конечное. Дадим определение предела функции, когда предел функции равен
, а предел функции b — число конечное. Дадим определение предела функции, когда предел функции равен 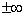 при х → а или
при х → а или 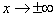 .
.
Функция 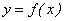 при х → а имеет своим пределом
при х → а имеет своим пределом 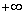 (или
(или 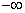 ), если, каково бы ни было
), если, каково бы ни было 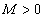 , найдется такое
, найдется такое 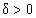 , что для всех x, для которых выполняется неравенство
, что для всех x, для которых выполняется неравенство 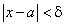 , будет выполняться неравенство
, будет выполняться неравенство 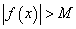 .
.
Символически это записывается так:
ris_01-07.gif
На рис. 1.7 приведены графики функций
приведены графики функций 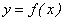 и
и 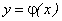 , которые имеют бесконечные пределы соответственно при стремлении аргумента x к конечному пределу а и бесконечному пределу +∞:
, которые имеют бесконечные пределы соответственно при стремлении аргумента x к конечному пределу а и бесконечному пределу +∞:
Для отыскания δ-окрестности точки a на оси Oу откладываем отрезок, равный M. Через точку (O, М) проводим прямую, параллельную оси Oх. Находим точку пересечения этой прямой с графиком функции . Находим абсциссу x1 точки пересечения А. За величину δ можно принять δ = |а — х1|.
Очевидно, для всех хϵ(а — δ, а) выполняется неравенство 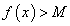 .
.
В определении предела функции
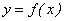 при х → а число b никак не связывалось со значением этой функции в точке х = а. Однако равенство b = f(a) является важнейшим свойством функции.
при х → а число b никак не связывалось со значением этой функции в точке х = а. Однако равенство b = f(a) является важнейшим свойством функции.
Функция 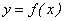 называется непрерывной в точке х = а
называется непрерывной в точке х = а , если она определена как в точке х = а, так и в некоторой ее окрестности; для произвольного
, если она определена как в точке х = а, так и в некоторой ее окрестности; для произвольного 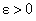 найдется такое
найдется такое 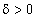 , что для всех x, удовлетворяющих условию
, что для всех x, удовлетворяющих условию 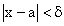 , будет выполняться неравенство
, будет выполняться неравенство 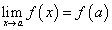 .
.
Символически это записывается так:
Из определения непрерывности функции в точке 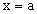 следует, что функция
следует, что функция 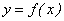 непрерывна в точке
непрерывна в точке 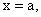 если:
если:
1) функция 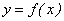 определена как в точке х = а, так и в некоторой ее окрестности;
определена как в точке х = а, так и в некоторой ее окрестности;
2) существуют односторонние пределы функции 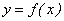 :
:
3) выполняются условия:
Дадим другое определение непрерывности функции, облегчающее проверку условия непрерывности функции. Обозначим через 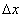 (приращение аргумента) разность между двумя значениями независимой переменной x:
(приращение аргумента) разность между двумя значениями независимой переменной x: 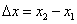 , где x1 — предыдущее значение, а x2 — последующее значение x. Очевидно,
, где x1 — предыдущее значение, а x2 — последующее значение x. Очевидно, 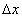 может быть величиной как положительной, так и отрицательной, ибо последующее значение может быть как больше, так и меньше предыдущего значения.
может быть величиной как положительной, так и отрицательной, ибо последующее значение может быть как больше, так и меньше предыдущего значения.
Обозначим через 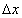 разность х — а:
разность х — а: 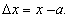 Разность
Разность 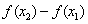 называется приращением функции и обозначается так:
называется приращением функции и обозначается так:
Также очевидно, что 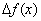 может быть величиной как положительной, так и отрицательной (рис. 1.8
может быть величиной как положительной, так и отрицательной (рис. 1.8 , 1.9
, 1.9 ).
).
По определению, если функция 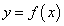 непрерывна в точке х = а, то:
непрерывна в точке х = а, то:
С учетом введенных обозначений имеем: 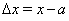 ;
; 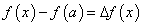 . Очевидно, при х → а приращение аргумента
. Очевидно, при х → а приращение аргумента 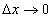 ; предел
; предел 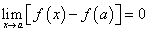 можно переписать следующим образом:
можно переписать следующим образом:
Из равенства (20) следует, что предел приращения непрерывной функции равен нулю, когда приращение аргумента стремится к нулю. Естественно, проделав все операции в обратном порядке, получим, что из равенства (20) следует непрерывность функции в точке х = а, т.е. равенство (20) является необходимым и достаточным условием непрерывности функции в точке х = а.
Так как 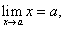 то равенство
то равенство 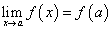 можно переписать следующим образом:
можно переписать следующим образом: 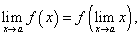 то есть предел от непрерывной функции равен знаку функции от предела аргумента.
то есть предел от непрерывной функции равен знаку функции от предела аргумента.
Если функция непрерывна в каждой точке множества M, то эта функция называется непрерывной на этом множестве .
.
Как нам известно, значение δ зависит как от ε, так и от точки х = а.
Если для всех точек непрерывности функции f(x), заданной на множестве М, величина δ будет зависеть только от ε, то такая функция на множестве М называется равномерно непрерывной . Выдающимся немецким математиком Г. Кантором доказано, что непрерывная функция на замкнутом множестве является равномерной непрерывной, то есть непрерывная функция у = f(х) на отрезке [а, b] является на этом отрезке равномерно непрерывной. Понятие равномерной непрерывности
. Выдающимся немецким математиком Г. Кантором доказано, что непрерывная функция на замкнутом множестве является равномерной непрерывной, то есть непрерывная функция у = f(х) на отрезке [а, b] является на этом отрезке равномерно непрерывной. Понятие равномерной непрерывности играет существенную роль в современном математическом анализе.
играет существенную роль в современном математическом анализе.
Рассмотрим типовые примеры доказательства непрерывности функций на основе введенного нами нового определения «непрерывность».
Пример 1. Доказать, что функция 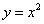 является непрерывной на множестве
является непрерывной на множестве  .
.
Доказательство. Пусть х — произвольная точка множества 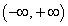 . Покажем, что для произвольного х будет выполняться равенство (20).
. Покажем, что для произвольного х будет выполняться равенство (20).
Доказательство проведем по шагам.
-
Берем произвольную точку х из множества
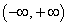 , придаем х приращение
, придаем х приращение 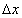 ; находим приращенное (новое) значение заданной функции:
; находим приращенное (новое) значение заданной функции: -
Находим приращение функции
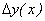 путем вычитания из нового значения функции ее старого (начального) значения (здесь старое значение функции есть
путем вычитания из нового значения функции ее старого (начального) значения (здесь старое значение функции есть 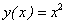 , новое значение функции есть
, новое значение функции есть 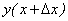 ):
): -
Находим предел:
Для ряда функций, удовлетворяющих дополнительным требованиям, легко устанавливается непрерывность с помощью теоремы, приведенной ниже.
Особыми требованиями являются монотонное возрастание или монотонное убывание.
Напомним, что монотонно возрастающие и монотонно убывающие функции называются монотонными .
.
Если при 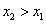
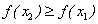 , то функция
, то функция 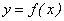 называется неубывающей
называется неубывающей , а при
, а при 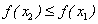 называется невозрастающей
называется невозрастающей .
.
Следующая теорема определяет непрерывную функцию на множестве M для монотонных функций.
Теорема 11. Если функция 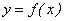 монотонна на множестве M и соответствующие ее значения сплошь заполняют промежуток Y, то функция
монотонна на множестве M и соответствующие ее значения сплошь заполняют промежуток Y, то функция 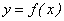 непрерывна на множестве M.
непрерывна на множестве M.
Здесь впервые применено новое понятие «сплошное заполнение промежутка», под которым понимается следующее: функция 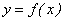 при изменении x на множестве M принимает все без исключения значения, находящиеся в промежутке Y.
при изменении x на множестве M принимает все без исключения значения, находящиеся в промежутке Y.
Например, функция 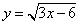 при
при 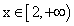 принимает все значения, находящиеся в промежутке
принимает все значения, находящиеся в промежутке 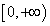 , т.е. значения заданной функции сплошь заполняют промежуток
, т.е. значения заданной функции сплошь заполняют промежуток 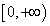 . Действительно, каково бы ни было
. Действительно, каково бы ни было 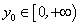 , из множества
, из множества 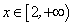 найдется такое значение x, для которого
найдется такое значение x, для которого 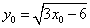 :
: 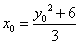 . Представив x0 в следующем виде
. Представив x0 в следующем виде 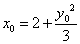 , убеждаемся, что
, убеждаемся, что 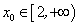 .
.
С помощью сформулированной теоремы легко устанавливается непрерывность основных элементарных функций, в области их монотонности. Например, показательная функция у = ах (а > 0, а ≠ 1) монотонна при 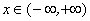 ; значения y сплошь заполняют промежуток
; значения y сплошь заполняют промежуток 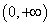 . Отсюда следует, что функция у = ах непрерывна на множестве
. Отсюда следует, что функция у = ах непрерывна на множестве 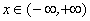 .
.
Из условий непрерывности функции в точке следует, что:
1) функция должна быть определена как в самой точке, так и в некоторой ее окрестности;
2) должны существовать односторонние пределы этой функции;
3) односторонние пределы должны быть равны между собой;
4) односторонние пределы равны значению функции в этой точке.
Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке . Наименование разрыва функции в точке зависит от того, какое из условий 1-4 не выполняется.
. Наименование разрыва функции в точке зависит от того, какое из условий 1-4 не выполняется.
В настоящем курсе точки разрыва делятся на две группы (два рода): точки разрыва первого рода и точки разрыва второго рода.
К точкам разрыва первого рода относятся точки, для которых не выполняется условие 4 (такая точка называется устранимой точкой разрыва
относятся точки, для которых не выполняется условие 4 (такая точка называется устранимой точкой разрыва ) или когда существуют односторонние пределы, но они не равны между собой (такая точка разрыва называется точкой разрыва с конечным скачком
) или когда существуют односторонние пределы, но они не равны между собой (такая точка разрыва называется точкой разрыва с конечным скачком ).
).
Односторонние пределы заданной функции при 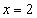 существуют и равны между собой: f(2 — 0) = 4, f(2 + 0) = 4, но не равны значению функции в точке Х = 2: f(2) = 2. Если предположить, что f(2) = 4, то разрыв будет устранен. Поэтому для заданной функции (21) точка
существуют и равны между собой: f(2 — 0) = 4, f(2 + 0) = 4, но не равны значению функции в точке Х = 2: f(2) = 2. Если предположить, что f(2) = 4, то разрыв будет устранен. Поэтому для заданной функции (21) точка 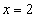 является устранимой точкой разрыва.
является устранимой точкой разрыва.
Пример 3. Рассмотрим функцию:
График заданной функции представлен на рис. 1.11 .
.
Заданная функция в точке x = 0 имеет односторонние пределы, которые не равны между собой:
f(0 — 0) = -1, f(0 + 0) =1.
Следовательно, точка x = 0 является точкой разрыва первого рода.
Заданная функция в точке x = 0 имеет односторонние пределы, которые не равны между собой:
f(0 — 0) = -1, f(0 + 0) =1.
Следовательно, точка x = 0 является точкой разрыва первого рода.
Скачком функции в точке х = а , называется модуль разности:
, называется модуль разности:
|f(a + 0) — f(a — 0)|.
Для заданной функции скачок в точке 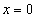 равен 2:
равен 2:
Точки, в которых не выполняются условие 1 или условие 2, относятся к точкам разрыва второго рода . В точках разрыва второго рода функция может иметь скачок, равный бесконечности. Например, функция
. В точках разрыва второго рода функция может иметь скачок, равный бесконечности. Например, функция 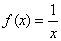 в точке x = 0 не определена, односторонние пределы функции в этой точке не являются конечными:
в точке x = 0 не определена, односторонние пределы функции в этой точке не являются конечными: 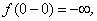
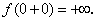 Скачок в точке x = 0 равен бесконечности:
Скачок в точке x = 0 равен бесконечности: 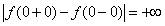 . Следовательно, точка x = 0 для заданной функции является точкой разрыва второго рода.
. Следовательно, точка x = 0 для заданной функции является точкой разрыва второго рода.
Первая теорема Больцано-Коши. Если функция 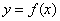 определена и непрерывна на отрезке [a, b] и на концах отрезка принимает значения разных знаков, то внутри отрезка [a, b] найдется по крайней мере хотя бы одна точка
определена и непрерывна на отрезке [a, b] и на концах отрезка принимает значения разных знаков, то внутри отрезка [a, b] найдется по крайней мере хотя бы одна точка 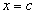 , где значение функции равно нулю:
, где значение функции равно нулю: 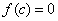 .
.
Теорема имеет простой геометрический смысл: непрерывная линия, имеющая концы по разные стороны оси 0х, непременно пересечет ось 0х хотя бы один раз (рис. 1.12 ).
).
На рис. 1.12 функция 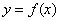 представлена своим графиком:
представлена своим графиком: 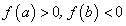 . График функции пересекает ось Ох в точке
. График функции пересекает ось Ох в точке 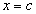 :
: 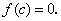
Вторая теорема Больцано-Коши. Если функция 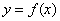 определена и непрерывна на отрезке [a, b] и на концах отрезка принимает неравные значения
определена и непрерывна на отрезке [a, b] и на концах отрезка принимает неравные значения 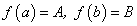 , то, каково бы ни было
, то, каково бы ни было 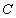 , находящееся между А и В
, находящееся между А и В 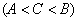 , на отрезке [a, b] найдется по крайней мере одна точка
, на отрезке [a, b] найдется по крайней мере одна точка 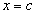 , для которой
, для которой 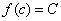 .
.
Для наглядности на рис. 1.13 представлен график функции, удовлетворяющий условиям теоремы. Заданная функция на графике имеет три точки
представлен график функции, удовлетворяющий условиям теоремы. Заданная функция на графике имеет три точки  находящиеся внутри отрезка [а, b], для которых выполняются равенства:
находящиеся внутри отрезка [а, b], для которых выполняются равенства:
Следствие. Если функция 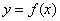 определена и непрерывна в каком-либо промежутке Х (замкнутом или нет, конечном или бесконечном), то принимаемые ею значения сами также заполняют сплошь некоторый промежуток.
определена и непрерывна в каком-либо промежутке Х (замкнутом или нет, конечном или бесконечном), то принимаемые ею значения сами также заполняют сплошь некоторый промежуток.
Первая теорема Вейерштрасса. Если функция 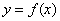 определена и непрерывна в замкнутом промежутке [a, b], то она ограничена и снизу, и сверху, то есть существуют такие постоянные и конечные числа
определена и непрерывна в замкнутом промежутке [a, b], то она ограничена и снизу, и сверху, то есть существуют такие постоянные и конечные числа  , что
, что 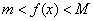 для всех
для всех 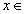 [a, b].
[a, b].
Теорема существования обратной функции. Если функция 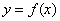 в области определения непрерывна и монотонна, то обратная функция
в области определения непрерывна и монотонна, то обратная функция 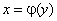 на множестве значений функции также монотонна и непрерывна.
на множестве значений функции также монотонна и непрерывна.
Теорема существования сложной функции. Сложная функция, составленная из любого конечного числа непрерывных функций, есть непрерывная функция.
Теорема 12. Если функции 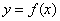 и
и 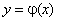 определены и непрерывны в замкнутом промежутке [a, b], то определены и непрерывны функции
определены и непрерывны в замкнутом промежутке [a, b], то определены и непрерывны функции 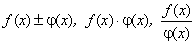 (последнее справедливо при условии, что
(последнее справедливо при условии, что 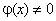 ).
).
Сформулированная теорема доказывается элементарно. Например, докажем справедливость того, что при непрерывности функций 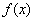 и
и 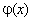 в замкнутом промежутке [a, b], где
в замкнутом промежутке [a, b], где 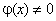 , функция
, функция 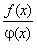 также непрерывна.
также непрерывна.
Действительно, пусть x0 — произвольная точка отрезка [a, b]. По условию теоремы функции 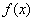 и
и 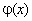 непрерывны в этой точке, то есть:
непрерывны в этой точке, то есть:
По теореме о пределе частного имеем:
Из полученного равенства следует, что функция 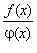 является непрерывной функцией в x0.
является непрерывной функцией в x0.
В силу произвольности взятой точки отсюда заключаем, что функция 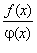 является непрерывной в замкнутом промежутке [a, b].
является непрерывной в замкнутом промежутке [a, b].
Рассмотрим типовые примеры приложения вышеизложенной теории.
Пример 4. Вычислить приращение аргумента и функции y = sinx, когда х изменяется от 0 до 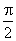 .
.
Решение. Первоначальное значение аргумента х = 0; приращенное значение аргумента 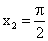 .
.
Приращение аргумента ∆х равно:
Приращенное значение функции y = sinx равно:
Приращение функции равно:
Пример 5. Найти приращение функции у = х2, соответствующее приращению ∆х, в точке х0.
-
Находим приращенное значение функции, соответствующее новому значению аргумента — х0 + ∆х:
у(х0 + ∆х) = (х0 + ∆х)2 = х02 + 2х0 ∙ ∆х + ∆х2.
-
Находим приращение функции:
∆у = у(х0 + ∆х) — у(х0) = х02 + 2х0 ∙ ∆х + ∆х2- х02 = 2х0∆х + ∆х2,
или ∆у = ∆х (2х0 + ∆х).
Пусть требуется найти приращенное значение и приращение функции у = х2, если аргумент х получил приращение ∆х = 0,5 в точке х = 2.
Решение. По условию задачи х0 = 2; ∆х = 0,5.
Приращенное значение функции равно:
у(2 + 0,5) = у(2,5) = (2,5)2 = 6,25.
Приращение функции равно:
∆у = у(2,5) — у(2) = (2,5)2 — 22 = 6,25 — 4 = 2,25.
Пример 6. Доказать, что функция у = х3 является непрерывной в промежутке (-∞; +∞).
Доказательство. Функция у = х3 определена на множестве (-∞; +∞).
Покажем, что бесконечно малому приращению аргумента из множества (-∞; +∞) соответствует бесконечно малое приращение функции. Зафиксируем произвольную точку х. Аргументу х дадим приращение ∆х. Найдем приращенное (новое) значение функции:
Находим приращение 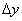 функции у = х3:
функции у = х3:
Переходя к пределу, получим:
Таким образом, бесконечно малому приращению аргумента в любой точке множества (-∞; +∞) соответствует бесконечно малое приращение функции, что является доказательством непрерывности функции у = х3 на множестве (-∞; +∞).
Пример 7. Доказать, что функция у = cosx непрерывна при х ϵ (-∞; +∞).
Фиксируем произвольное х из множества (-∞; +∞).
-
Придадим х приращение ∆х; найдем приращенное значение функции:
у (х + ∆х) = cos(х + ∆х).
-
Находим приращение функции:
-
Находим предел:
Так как |sinα| ≤ α и |sinα| ≤ 1, то:
Отсюда следует, что 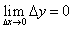 , т.е. функция
, т.е. функция 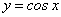 непрерывна на множестве (-∞; +∞).
непрерывна на множестве (-∞; +∞).
Контрольные вопросы
-
Дайте определение предела функции.
-
Дайте определение непрерывности функции.
-
Зависит ли δ в определении непрерывности функции от точки, где устанавливается непрерывность при заданном ε?
-
Как называется непрерывная функция, если для всех точек множества ее определения для заданного ε можно подобрать одно и то же δ?
-
Какие должны выполняться условия для непрерывности функции у = f(х) в т. х = х0?
-
Какая точка называется точкой разрыва функции и какие точки разрыва вы знаете?
-
Каковы условия непрерывности монотонных функций?
-
Дайте определение точки разрыва функции.
-
Приведите классификацию точек разрыва.
-
Назовите свойства функций, непрерывных на замкнутом интервале.
Задания для самостоятельной работы
-
Напишите последовательность значений:
-
Пользуясь определением предела последовательности, докажите, что:
-
(Указание. Положить x = 3 + α, где α — б.м.в.)
-
Используя теоремы о пределах, найдите пределы:
-
Найдите точки разрыва функции
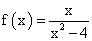 и исследуйте поведение функции в окрестностях точек разрыва (т. е. найдите односторонние пределы в точке разрыва).
и исследуйте поведение функции в окрестностях точек разрыва (т. е. найдите односторонние пределы в точке разрыва). -
Пользуясь определением непрерывности функций, докажите, что функция
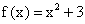 непрерывна: 1) в точке x = 1; 2) при
непрерывна: 1) в точке x = 1; 2) при 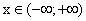 .
. -
Найдите точки разрыва и исследуйте их характер для следующих функций:
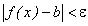 . (16)
. (16)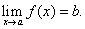 (17)
(17)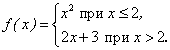 (18)
(18)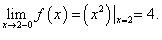
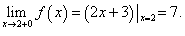
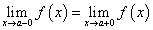 .
.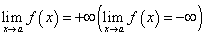 .
.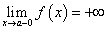 ,
, 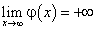 .
.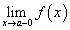 ,
, 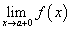 ;
;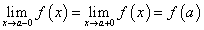 .
.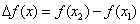 .
.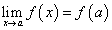 , или
, или 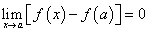 .
.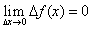 . (20)
. (20)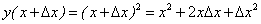 .
.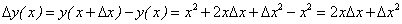 .
.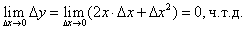
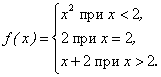 (21)
(21)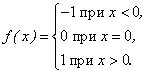 (22)
(22)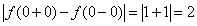 .
.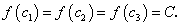
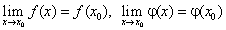 .
.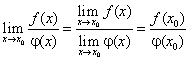 .
.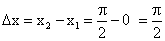 .
.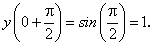
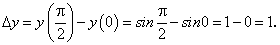
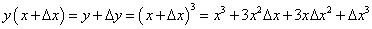 .
.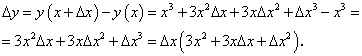
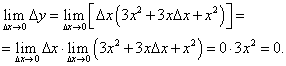
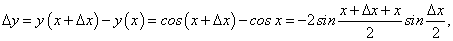
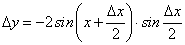 .
.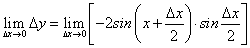 .
.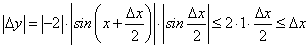 .
.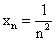 ;
;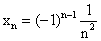 ;
;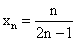 ;
;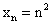 .
.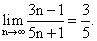
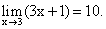
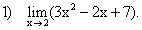
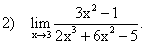
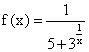 при
при 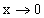 .
.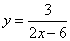 ;
;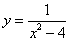 ;
;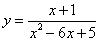 ;
;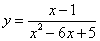 .
.
