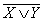Успешно изучив материал, Вы будете знать:
-
понятие высказывания;
-
истинность и ложность высказывания;
-
сложные и простые высказывания;
-
понятие операций над высказываниями;
-
диаграммы Эйлера—Венна;
-
применение и построение таблиц истинности;
-
применение логических элементов в компьютере.
После изучения данной темы Вы будете уметь:
-
составлять сложные высказывания из набора простых;
-
проверять истинность и ложность сложных высказываний;
-
использовать диаграммы для иллюстрации операций над высказываниями.
После изучения материала Вы будете обладать навыками:
-
построения логических выражений;
-
решения логических задач.
Логика как наука сформировалась в IV в. до н.э. Ее создал древнегреческий ученый Аристотель, его ученики и последователи. Аристотель исследовал различные формы суждений и их комбинации и ввел понятие силлогизма — рассуждения, в котором из двух заданных рассуждений вида «все a суть b», «некоторые a суть b», «все a не суть b», «не все a суть b» выводится третье. Силлогизмы бывают правильными и неправильными. Пример правильно силлогизма: «Все ноутбуки — компьютеры. Все компьютеры имеют процессор. Следовательно, все ноутбуки имеют процессор». Пример неправильного силлогизма: «Все компьютеры являются электрическими приборами. Некоторые электрические приборы являются утюгами. Значит — некоторые компьютеры являются утюгами». Доказано, что общее число силлогизмов, которые можно составить из суждений указанного вида, равно 256, из них правильных всего 24. В XVIII в. великий математик Эйлер предложил очень простой метод проверки правильности силлогизмов — метод геометрической иллюстрации логических рассуждений, который впоследствии был назван диаграммами Эйлера—Венна
— рассуждения, в котором из двух заданных рассуждений вида «все a суть b», «некоторые a суть b», «все a не суть b», «не все a суть b» выводится третье. Силлогизмы бывают правильными и неправильными. Пример правильно силлогизма: «Все ноутбуки — компьютеры. Все компьютеры имеют процессор. Следовательно, все ноутбуки имеют процессор». Пример неправильного силлогизма: «Все компьютеры являются электрическими приборами. Некоторые электрические приборы являются утюгами. Значит — некоторые компьютеры являются утюгами». Доказано, что общее число силлогизмов, которые можно составить из суждений указанного вида, равно 256, из них правильных всего 24. В XVIII в. великий математик Эйлер предложил очень простой метод проверки правильности силлогизмов — метод геометрической иллюстрации логических рассуждений, который впоследствии был назван диаграммами Эйлера—Венна (рис. 19.1
(рис. 19.1 ). Согласно этому методу, каждое суждение можно изобразить в виде геометрической фигуры. Так, суждение «все a суть b» изображено на рисунке 19.1(1), «некоторые a суть b» — на рисунке 19.1(2), «все a не суть b» — на рисунке 19.1(3), и «не все a суть b» — на рисунке 19.1(4)
). Согласно этому методу, каждое суждение можно изобразить в виде геометрической фигуры. Так, суждение «все a суть b» изображено на рисунке 19.1(1), «некоторые a суть b» — на рисунке 19.1(2), «все a не суть b» — на рисунке 19.1(3), и «не все a суть b» — на рисунке 19.1(4)
Логика, основанная на теории силлогизмов, называется классической логикой . В течение многих веков логика практически не развивалась, и лишь в XVI в. немецкий ученый Лейбниц задумал создать новую логику, в которой каждому понятию соответствовал бы символ, а рассуждения имели вид вычислений. Только в середине XIX в. эти идеи воплотил в жизнь Дж. Буль, который создал алгебру логики. С этого времени начала развиваться новая наука — математическая логика
. В течение многих веков логика практически не развивалась, и лишь в XVI в. немецкий ученый Лейбниц задумал создать новую логику, в которой каждому понятию соответствовал бы символ, а рассуждения имели вид вычислений. Только в середине XIX в. эти идеи воплотил в жизнь Дж. Буль, который создал алгебру логики. С этого времени начала развиваться новая наука — математическая логика , которая использует язык и методы математики.
, которая использует язык и методы математики.
Основным понятием математической логики является высказывания.
Высказывание — любое повествовательное предложение, про которое известно, является оно истинным или ложным.
— любое повествовательное предложение, про которое известно, является оно истинным или ложным.
Например, являются высказываниями:
1) «сумма чисел 2 и 5 равна 7» (истинное высказывание);
2) «2 + 5 = 7» — предыдущее высказывание, записанное с помощью математических символов;
3) «для всех значений x верно неравенство x2 + 1 < 0» (ложное высказывание);
4) «завтра будет солнечный день» (может быть истинным или ложным).
Высказывания обозначаются заглавными буквами латинского алфавита — A, B и т.д.
Не всякое предложение является высказыванием, например, восклицательные или побудительные предложения не являются высказываниями. Также не являются высказываниями определения — они лишь дают название некоторому объекту, но не могут быть истинными или ложными. Кроме высказываний существуют еще высказывательные формы — предложения, содержащие переменную. Например, выражение «x2
— 1 > 0» является высказывательной формой, так как при некоторых значениях переменной эта форма становится истинным высказыванием, а при других значениях — ложным.
— предложения, содержащие переменную. Например, выражение «x2
— 1 > 0» является высказывательной формой, так как при некоторых значениях переменной эта форма становится истинным высказыванием, а при других значениях — ложным.
Выше мы говорили, что высказывание имеет вид повествовательного предложения. Из двух таких предложений можно получить новые с помощью логических связок — союзов «и», «или», «если…, то», «тогда и только тогда, когда» и частицы «не». Такие предложения будем называть составными. Предложения, не являющиеся составными, называются элементарными. Соответственно, если можно судить об истинности или ложности таких предложений, то они будут называться простыми
— союзов «и», «или», «если…, то», «тогда и только тогда, когда» и частицы «не». Такие предложения будем называть составными. Предложения, не являющиеся составными, называются элементарными. Соответственно, если можно судить об истинности или ложности таких предложений, то они будут называться простыми и составными высказываниями
и составными высказываниями . Например, высказывание «число делится на три тогда и только тогда, когда сумма цифр этого числа делится на три» является составным высказыванием (оно является истинным и в математике известно как признак делимости числа на три).
. Например, высказывание «число делится на три тогда и только тогда, когда сумма цифр этого числа делится на три» является составным высказыванием (оно является истинным и в математике известно как признак делимости числа на три).
С точки зрения грамматики различают простые и сложные предложения. Например, предложение «число 10 делится на 2 и на 5» является простым, хотя с точки зрения математической логики это — сложное высказывание, состоящее из двух простых высказываний «число 10 делится на 2», «число 10 делится на 5», полученное с помощью логической связки «и».
Аналогично тому, как в алгебре чисел используются операции сложения, вычитания, умножения, деления, в алгебре высказываний вводятся специальные операции, которые имеют названия логического сложения (дизъюнкции), логического умножения (конъюнкции), отрицания, импликации и эквиваленции. Рассмотрим эти операции подробно.
Пусть А и В — произвольные высказывания. Введем символ ˄ для обозначения логической связки «и». Сложное высказывание «А и В» считается истинным лишь в том случае, если оба исходных высказывания истинны. Если же хотя бы одно из исходных высказываний ложно, то сложное высказывание «А и В» считают ложным.
Высказывание «А и В», истинное, если истинны оба высказывания А и В, и ложное, если хотя бы одно из них ложно, называется конъюнкцией этих высказываний и обозначается А ˄ В.
этих высказываний и обозначается А ˄ В.
Запишем это определение в специальной форме, которая называется таблицей истинности. В ней для каждого значения истинности «И» (истина) или ложности «Л» (ложь) логических высказываний А и В определяется значение истинности высказывания А ˄ В.
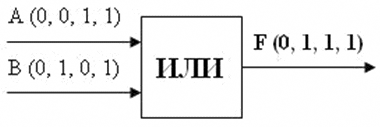
Введем символ ˅ для обозначения логической связки «или». Сложное высказывание «А или В» условимся считать ложным в том и только в том случае, когда оба высказывания А и В ложны.
Высказывание «А или В», истинное, если истинно хотя бы одно из высказываний А или В, и ложное лишь в одном случае, когда оба высказывания А и В ложны, называется дизъюнкцией этих высказываний и обозначается А ˅ В.
этих высказываний и обозначается А ˅ В.
Таблица истинности для высказывания А ˅ В выглядит следующим образом:
А |
В |
А˅В |
И |
И |
И |
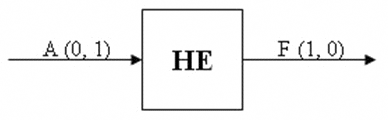
Логическая операция, соответствующая логической связке «не», называется отрицанием.
Высказывание «не А», истинное лишь в том случае, когда высказывание А ложно и ложное лишь в том случае, когда высказывание А истинно, называется отрицанием А и обозначается
А и обозначается 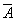 .
.
Таблица истинности для высказывания 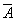 выглядит следующим образом:
выглядит следующим образом:
А |
В |
И |
Л |
Логические рассуждения чаще всего имеют форму цепочки высказываний. Эти высказывания имеют условный характер, то есть утверждают, что некоторое высказывание истинно при условии, что истинно другое высказывание. Например, «если два угла одного треугольника соответственно равны двум углам другого треугольника, то эти треугольники подобны». В общем виде такого рода высказывания записываются следующим образом «если А, то В» и называются импликацией . Высказывание А в этом случае называют условием, а высказывание В — заключением.
. Высказывание А в этом случае называют условием, а высказывание В — заключением.
Импликацией высказываний А и В называют высказывание A → B(читается «если А, то В»), ложное лишь в случае, когда А истинно, а В — ложно.
Таблица истинности для высказывания A → B выглядит следующим образом:
А |
В |
A>B |
И |
И |
И |
Эквиваленцией высказываний А и В называют высказывание A ↔ B (читается «А тогда и только тогда, когда В»), истинное, в том и только в том случае, когда оба эти высказывания истинны, или оба ложны.
высказываний А и В называют высказывание A ↔ B (читается «А тогда и только тогда, когда В»), истинное, в том и только в том случае, когда оба эти высказывания истинны, или оба ложны.
Таблица истинности для высказывания A ↔ B выглядит следующим образом:
А |
В |
A-B |
И |
И |
И |
Из данных высказываний А, В, С можно с помощью логических операций составить новые высказывания, которые будут истинны или ложны. Раздел математической логики, в котором изучают свойства выражений, составленных из высказываний с помощью логических операций, называется алгеброй высказываний .
.
Пусть X, Y, Z — переменные, обозначающие элементарные логические высказывания или их значения истинности. Такие переменные будем называть логическими (или высказывательными) переменными. С помощью логических переменных и символов логических операций можно формализовать любое логическое высказывание. Таким образом, логическое высказывание заменяется формулой, отражающей логическую структуру этого высказывания. Например, высказывание «Число а делится на 6 тогда и только тогда, когда а делится на 2, и а делится на 3» формализуется в виде 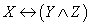 .
.
Дадим теперь строгое математическое определение формулы логики высказываний. Это определение имеет вид конструктивного (или индуктивного) определения.
Определим алфавит, то есть, набор символов, которые употребляются в логике высказываний:
-
X, Y, Z, Xi , Yi , Zi (i — индекс, значения которого — натуральные числа) — символы для обозначения логических переменных;
-
И, Л — символы, обозначающие логические константы «истина», «ложь»;
-
(,) — скобки, вспомогательные символы, служащие для указания порядка выполнения логических операций.
Дадим определение формулы логики высказываний .
.
-
Всякая логическая переменная есть формула.
-
Символы И, Л есть формулы.
-
Никаких других формул в логике высказываний нет.
Для формализации высказываний используют следующий алгоритм.
-
Если высказывание — простое, то ему ставится в соответствие элементарная формула.
-
Если высказывание — составное, то для составления формулы требуется:
-
выделить все элементарные высказывания и логические связки, образующие данное высказывание;
-
заменить их соответствующими символами;
-
расставить скобки в соответствии со смыслом данного высказывания.
-
Пример 1.
Формализовать высказывания:
а) «Неверно, что число 500 делится на 3 или на 13»;
б) «|a| ≤ 2 тогда и только тогда, когда -2 ≤ a ≤ 2».
Решение.
а) Обозначим простые высказывания: X — «число 500 делится на 3», Y — «число 500 делится на 13». Тогда данное сложное высказывание имеет вид 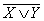 ;
;
б) Обозначим простые высказывания: X — «|a| ≤ 2 », Y — «a ≥ -2», Z — «a ≤ 2». Тогда данное высказывание имеет вид 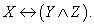
Пусть F — некоторая формула логики высказываний. Если каждой переменной, входящей в эту формулу, приписать одно из значений истинности, то, пользуясь таблицами истинности логических операций, можно найти значение истинности и формулы F при заданном наборе значений ее переменных. Это можно сделать, построив граф вершинами которого будут логическая переменная или логическая формула, а над ребрами графа проставим значения истинности каждого высказывания. Например, найдем значения истинности формул примера 1а).
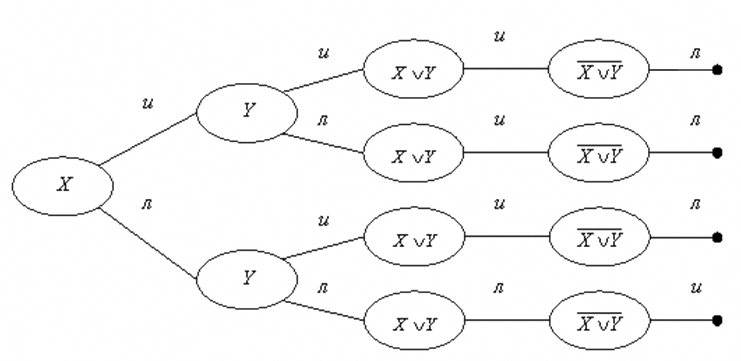
Наиболее удобной формой записи является таблица истинности.
Пример 2.
Найдем значения истинности формул примера 1.
Решение.
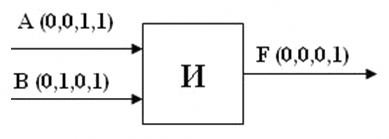
Базовые логические элементы реализуют три основные логические операции:
-
«И» — логическое умножение;
-
«ИЛИ» — логическое сложение;
-
«НЕ» — логическое отрицание (инверсия).
Любые устройства компьютера, производящие обработку или хранение информации, собраны из базовых логических элементов как из кирпичиков.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс — 1, нет импульса — 0. На вход логических элементов поступают сигналы-аргументы, на выходе появляется сигнал-функция.
Преобразование сигнала логическим элементом задается таблицей состояния (таблицей истинности данной функции).
На входы А и В логического элемента последовательно подаются четыре пары сигналов различных значений, на выходе получается последовательность из четырех сигналов, значения которых определяются в соответствии с таблицей истинности операции логического умножения.
На входы А и В логического элемента последовательно подаются четыре пары сигналов различных значений, на выходе получается последовательность из четырех сигналов, значения которых определяются в соответствии с таблицей истинности операции логического сложения.
На вход А логического элемента последовательно подаются два сигнала, на выходе получается последовательность из двух сигналов, значения которых определяются в соответствии с таблицей истинности операции логической инверсии (отрицания).
В целях упрощения работы компьютера все математические операции процессоре сводятся к сложению двоичных чисел, поэтому главной частью процессора является сумматор.
При сложении двоичных чисел образуется сумма в данном разряде, но при этом возможен перенос в старший разряд (1 + 1).
Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд.
Слагаемые |
Перенос |
Сумма |
|
А |
В |
Р |
S |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Из таблицы видно, что перенос реализуется с помощью операции логического умножения:
Р = А & В
Получим формулу для вычисления суммы. Значения суммы почти совпадают с результатом операции логического сложения (кроме случая, когда на входе две единицы, а на выходе — 0). Необходимый результат достигается, если результат логического сложения умножить на инвертированный перенос.
S = (A ˅ B) & не (A & B)
Чтобы убедиться в правильности данного предположения, построим таблицу истинности логического выражения.
А |
В |
А ˅ В |
А & В |
не(А & В) |
F = (А ˅ В)& не(А & В) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему полусумматора (рис. 19.2 ).
).
Полный одноразрядный сумматор должен иметь три входа: А, В — слагаемые и P0 — перенос из младшего разряда и два выхода — сумма S и перенос Р.
Слагаемые |
Перенос из младшего разряда |
Перенос |
Сумма |
|
А |
В |
Р0 |
Р |
S |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Идея построения полного сумматора такая же, как и у полусумматора.
Р = (A & B) ˅ (A & P0 ) ˅ (B & P0 )
S = (A ˅ B ˅ P0 ) & Р
Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. Выход (перенос) сумматора младшего разряда подключен к входу сумматора старшего разряда.
Важнейшим элементом оперативной памяти компьютера является триггер — устройство, позволяющее запоминать, хранить и считывать информацию. Каждый триггер может хранить 1 бит информации. Он имеет следующую логическую структуру (рис. 19.3
— устройство, позволяющее запоминать, хранить и считывать информацию. Каждый триггер может хранить 1 бит информации. Он имеет следующую логическую структуру (рис. 19.3 ).
).
В обычном состоянии на входы триггера подается сигнал 0 (сигнал отсутствует) и хранится как 0. Для записи на вход S подается сигнал 1, триггер его запоминает и хранит. Чтобы сбросить информацию, подают сигнал 1 на вход R, после чего триггер возвращается к исходному нулевому состоянию.
Основные выводы
-
Основным понятием математической логики является высказывание
 — любое повествовательное предложение, про которое известно, является оно истинным или ложным.
— любое повествовательное предложение, про которое известно, является оно истинным или ложным. -
Сложные высказывания можно получить из простых с помощью логических связок — союзов «и», «или», «если…, то», «тогда и только тогда, когда» и частицы «не».
-
Аналогично тому, как в алгебре чисел используются операции сложения, вычитания, умножения, деления, в алгебре высказываний вводятся специальные операции, которые имеют названия логического сложения (дизъюнкции), логического умножения (конъюнкции), отрицания, импликации и эквиваленции.
-
Из данных высказываний А, В, С можно с помощью логических операций составить новые высказывания, которые будут истинны или ложны. Раздел математической логики, в котором изучают свойства выражений, составленных из высказываний с помощью логических операций, называется алгеброй высказываний.
-
Пусть F — некоторая формула логики высказываний. Если каждой переменной, входящей в эту формулу, приписать одно из значений истинности, то, пользуясь таблицами истинности логических операций, можно найти значение истинности и формулы F при заданном наборе значений ее переменных. Это можно сделать, построив граф вершинами которого будут логическая переменная или логическая формула, а над ребрами графа проставим значения истинности каждого высказывания.
-
Базовые логические элементы реализуют три основные логические операции:
-
«И» — логическое умножение;
-
«ИЛИ» — логическое сложение;
-
«НЕ» — логическое отрицание (инверсия).
Любые устройства компьютера, производящие обработку или хранение информации, собраны из базовых логических элементов как из кирпичиков.
-
Контрольные вопросы
-
Что такое высказывание?
-
Какие бывают операции над высказываниями?
-
Для чего служат таблицы истинности?
-
Что такое сумматор?
-
Подумайте, какая связь между действиями над множествами и над высказываниями.
Литература и интернет-источники
-
Алехина Г.В., Годин И.М., Пронкин П.Г. и др. Информатика и математика: учебник — М.: МФПА, 2009.
-
http://www.fizmat.vspu.ru/books/informaticsshau/theory/chapter5/1_5.html
Задания для самостоятельной работы
Выполните задания к теме 19 в тетради-практикуме.
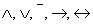 — символы логических операций;
— символы логических операций;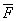 есть формула.
есть формула.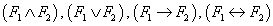 есть формулы.
есть формулы.