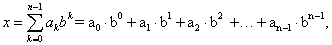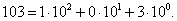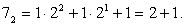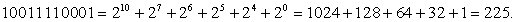Успешно изучив материал, Вы будете знать:
-
понятие системы счисления;
-
общий вид числа в системе с заданным базисом;
-
способы записи чисел в разных системах счисления;
-
системы счисления, используемые в информатике;
-
способы перевода из одной системы счисления в другую;
-
системы счисления, используемые в компьютере.
После изучения данной темы Вы будете уметь:
-
записать число в разных системах счисления;
-
переводить двоичный код числа в 8- и 16-ричный и наоборот;
-
использовать двоичную систему для решения прикладных задач.
После изучения материала Вы будете обладать навыками перевода чисел из одной системы счисления в другую.
Натуральные числа — целые положительные числа и (иногда) число ноль.
— целые положительные числа и (иногда) число ноль.
Множество натуральных чисел — бесконечно, т.е. для любого, сколь угодно большого числа N существует натуральное число N + 1.
Как можно записать такое количество чисел? Первые десять натуральных чисел мы записываем с помощью специальных знаков 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Однако продолжать так дальше неудобно — потребовалось запомнить слишком много знаков. Поэтому применяют наборы знаков для записи. Системы записи чисел (системы счисления) делятся на позиционные и непозиционные.
делятся на позиционные и непозиционные.
В непозиционных системах знак соответствует определенной величине, независимо от места в строке. Каноническим примером непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы:
I обозначает 1,
V — 5,
X — 10,
L — 50,
C — 100,
D — 500,
M — 1000.
Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе На самом деле римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из нее, например: IV = 4, в то время как: VI = 6.
На самом деле римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из нее, например: IV = 4, в то время как: VI = 6.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счетом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших ее у мусульман.
Каждая позиционная система счисления определяется некоторым целым числом b > 1 (т.н. основание системы счисления ), таким, что b единиц в каждом разряде объединяется в одну единицу следующего по старшинству разряда. Система счисления с основанием b также называется b-ричной.
), таким, что b единиц в каждом разряде объединяется в одну единицу следующего по старшинству разряда. Система счисления с основанием b также называется b-ричной.
Число x в b-ричной системе счисления представляется в виде линейной комбинации степеней числа b:
где ak
— это целые числа, называемые цифрами, удовлетворяющие неравенству 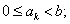
k — порядковый номер разряда начиная с нулевого;
n — число разрядов;
b — базис системы счисления.
Каждая степень bk в такой записи называется разрядом, старшинство разрядов и соответствующих им цифр определяется значением показателя k. Обычно для ненулевого числа x требуют, чтобы старшая цифра an-1 в b-ричном представлении x была также ненулевой.
Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число x записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо: x = an-1 an-1 … a0 .
Например, число сто три представляется в десятичной системе счисления в виде:
Наиболее употребимыми в настоящее время позиционными системами являются:
-
2 — двоичная
 (в дискретной математике, информатике, программировании);
(в дискретной математике, информатике, программировании); -
10 — десятичная система счисления (принятая повсеместно);
-
16 — шестнадцатеричная (наиболее часто используется в программировании, а также в шрифтах);
-
60 — шестидесятеричная (измерение углов и, в частности, долготы и широты.
Базисом двоичной системы является двойка. Для записи любого числа достаточно два знака: 0 и 1. Двоичная арифметика очень проста:
0 + 1 = 1 |
1 + 1 = 10 |
0*1 = 0 |
1*1 = 1 |
0/1 = 0 |
1/1 = 1. |
Как видно из таблицы, самая сложная операция — сложение. В нее входит умножение и сложение по модулю 2 (т.е. сложение с отбрасывание единиц старших разрядов)
Если отвлечься от технических деталей, то именно с помощью этих операций и выполняются все операции в компьютере. Для выполнения сложения однобитовых чисел делают обычно даже специальный логический элемент с двумя входами x, y и двумя выходами w, v, как бы составленный из элемента умножения (его часто называют конъюнкцией , чтобы не путать с умножением многозначных чисел) и элемента сложения по модулю 2. Этот элемент часто называют полусумматором
, чтобы не путать с умножением многозначных чисел) и элемента сложения по модулю 2. Этот элемент часто называют полусумматором , и о нем будет идти речь в следующей теме.
, и о нем будет идти речь в следующей теме.
Двоичная система используется в компьютерах, потому что она имеет ряд преимуществ перед другими системами:
-
для ее реализации нужны технические устройства с двумя устойчивыми состояниями («есть ток» — «нет тока», «намагничен» — «не намагничен» и т.п.), а не, например, с десятью, — как в десятичной;
-
представление информации посредством только двух состояний надежно и помехоустойчиво;
-
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
-
двоичная арифметика намного проще десятичной.
Несмотря на удобство счета в двоичной системе, записанные числа занимают много места. Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, 3-я и 4-я степень двух).
Таблица перевода для 8-ричного числа:
0 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Для 16-ричных чисел нужно 16 знаков, поэтому используют десятичные обозначения для первых 10-ти знаков, а вместо остальных пишут буквы A, B, C, D, E, F.
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 0 1 2 3 4 5 6 7 8 9 A B C D E F
Используя таблицу, легко записать двоичное число в 16-ричной системе: 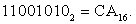
Переводить в эти системы можно и методом, описанным выше для 2-чной системы.
Для перевода двоичного числа в десятичное следует разложить его на разряды и складывать 2 в степени (№ разряда — 1)
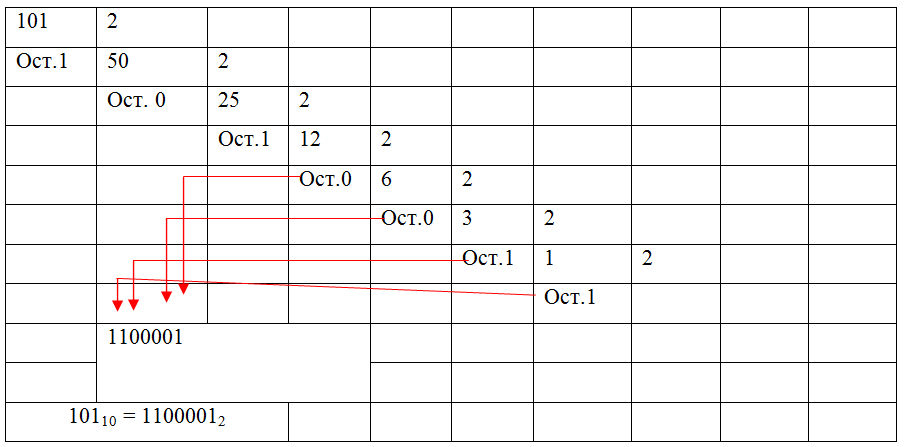
Для перевода 10-го числа в двоичное его надо последовательно делить на 2, а остатки от деления записать в обратном порядке:
Для перевода чисел из одной системы счисления в другую можно воспользоваться калькулятором, входящим в стандартные программы Windows. Выберите «Вид → Инженерный» (рис. 18.1 ). Задайте первоначальную систему счисления: Bin, Oct, Dec, Hex (соответственно: двоичная, восьмеричная, десятиричная и шестнадцатиричная), введите число в этой системе и переключите калькулятор на нужную систему счисления.
). Задайте первоначальную систему счисления: Bin, Oct, Dec, Hex (соответственно: двоичная, восьмеричная, десятиричная и шестнадцатиричная), введите число в этой системе и переключите калькулятор на нужную систему счисления.
Основные выводы
-
Системы записи чисел (системы счисления)
 делятся на позиционные и непозиционные. В непозиционных системах знак соответствует определенной величине, независимо от места в строке. В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.
делятся на позиционные и непозиционные. В непозиционных системах знак соответствует определенной величине, независимо от места в строке. В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. -
В двоичной системе существует только 2 знака 0 и 1. Двоичная арифметика намного проще десятичной, но из-за громоздкости не используется вне компьютеров.
-
Часто вместо двоичной используются 8- и 16-ричнная системы счисления. Существуют простые алгоритмы перевода чисел из одной системы счисления в другую.
Контрольные вопросы
-
Что такое система счисления?
-
Чем отличается арабская и римская запись чисел?
-
Какой общий вид записи числа в системе с заданным базисом?
-
Какая система счисления используется в компьютерах и почему?
-
Чем удобны 8- и 16-ричные системы?
-
Подумайте, почему в 16-ричном коде числа присутствуют буквы.
Литература и интернет-источники
-
Алехина Г.В., Годин И.М., Пронкин П.Г. и др. Информатика и математика: учебник — М.: МФПА, 2009.
Задания для самостоятельной работы
Выполните задания к теме 18 в тетради-практикуме.