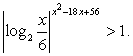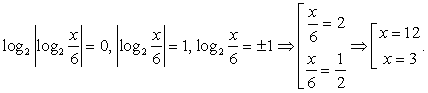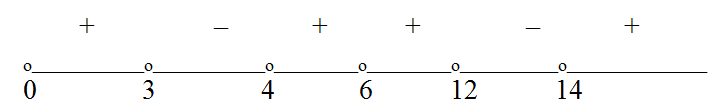Комментарий. При решении логарифмических уравнений, так же, как в случаях иррациональных уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому и проверка корней логарифмического уравнения осуществляется либо непосредственно по предварительно найденной области определения, либо по условиям ее задающим (подстановкой в соответствующую систему неравенств). Заметим, что иногда удобно осуществить проверку и непосредственной подстановкой найденных корней в исходное логарифмическое уравнение. Это, конечно же, допустимо. Естественно, что при решении логарифмических уравнений возможно и следование стратегии равносильных преобразований. Далее мы рассмотрим примеры решения разного рода.
Расширение области определения при решении логарифмических уравнений связано, как правило, с двумя обстоятельствами:
1) преобразование потенцирования («отбрасывания» логарифмов, замена уравнения уравнением );
2) использование «справа — налево» формул:
Область определения левой части этих формул может быть шире области определения правой их части.
Заметим, что применение этих формул «слева — направо» вообще следует избегать, т.к. это может привести к сужению области определения уравнения и потере корней.
Пример 8.1.
Решение
Будем представлять правую часть уравнения последовательно в виде логарифмов с основаниями 4, 2 и 3 и проводить преобразование потенцирования:
Проверим найденное значение непосредственной подстановкой в исходное уравнение:
Мы пришли к верному числовому равенству. Таким образом, x = 41 — единственный корень данного уравнения.
Ответ:  41.
41.
Пример 8.2.
Решение
Представим 1 как lg10 и преобразуем левую и правую части уравнения, исходя из свойств логарифмов:
Потенцируя уравнение, получаем:
Решим это рациональное уравнение:
Осуществим проверку корней. Область определения исходного уравнения задается условиями: 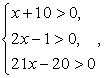 т.е. область определения
т.е. область определения 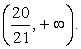 Оба корня, очевидно, принадлежат области определения. Таким образом, корни данного уравнения
Оба корня, очевидно, принадлежат области определения. Таким образом, корни данного уравнения 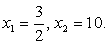
Ответ:  1,5; 10.
1,5; 10.
Пример 8.3.
Решение
Пусть 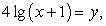 тогда получаем систему уравнений:
тогда получаем систему уравнений:
Корни первого уравнения системы: 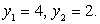 Тогда исходное уравнение равносильно совокупности:
Тогда исходное уравнение равносильно совокупности:
Потенцируя полученные уравнения приходим к выводу, что х = 9 или 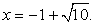 Оба этих значения являются корнями данного уравнения, поскольку его область определения задается условием х + 1 > 0, т.е. х > -1.
Оба этих значения являются корнями данного уравнения, поскольку его область определения задается условием х + 1 > 0, т.е. х > -1.
Комментарий. Если в уравнении содержаться логарифмы с разными основаниями, то следует привести их к одному основанию, воспользовавшись формулами перехода к новому основанию логарифма:
Пример 8.4.
Решение
В данном уравнении перейдем к логарифмам по основанию 2:
Последнее уравнение равносильно системе: 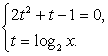
Корни первого уравнения системы: 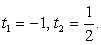 Таким образом, имеем совокупность уравнений
Таким образом, имеем совокупность уравнений 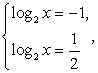 которая равносильна системе:
которая равносильна системе: 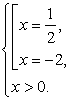
Откуда очевидно, что 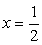 — единственный корень данного уравнения.
— единственный корень данного уравнения.
Заметим, что применение формул перехода к новому основанию логарифма, как правило, приводит к изменению области определения уравнения. Поэтому, следует анализировать в ходе решения, как возможность, появления посторонних корней, так и возможность потери корней.
Ответ:  0,5.
0,5.
Пример 8.5.
Решение
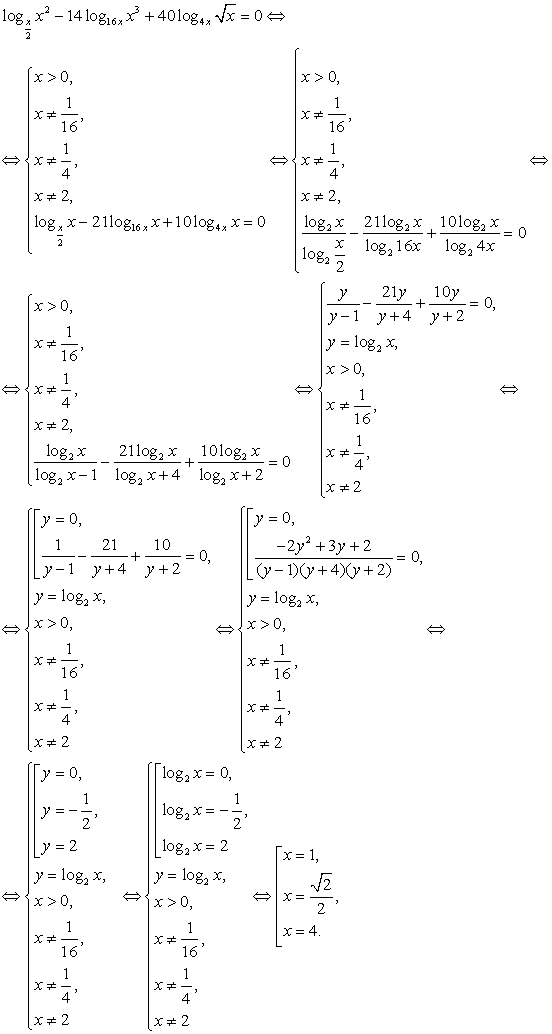
Прежде всего, воспользуемся известным свойством логарифма и получим одинаковое для всех логарифмов логарифмируемое выражение:
Теперь воспользуемся формулой перехода к новому основанию логарифма, получаем:
Далее имеем:
Корни второго уравнения системы: 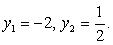 Следовательно, решение исходного уравнения свелось к решению совокупности:
Следовательно, решение исходного уравнения свелось к решению совокупности:
Решим первое уравнение совокупности:
Аналогично, решая второе уравнение совокупности, получаем х = 4.
Найдем, теперь область определения исходного уравнения и проведем проверку корней: 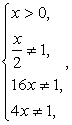 т.е.
т.е. 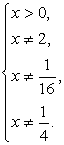
Ясно, что оба найденных значения х удовлетворяют области определения.
Наконец, следует проанализировать возможную потерю корней. Для этого выясним, когда наши преобразования приводили к сужению области определения уравнения. После перехода к новому основанию логарифма дальнейшее решение осуществляется при условии: x > 0 и x ≠ 1. Дополнительное условие x ≠ 1 не имеет отношения к исходному уравнению, поэтому х = 1 — возможный потерянный корень. Подставив значение х = 1 в исходное уравнение, убеждаемся, что это действительно корень. Таким образом, корни исходного уравнения: 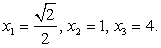
Комментарий. Применяя при решении логарифмических уравнений формулы перехода к новому основанию целесообразней переходить к новому основанию, не являющемуся выражением с переменной, а равному некоторому числу. Как правило, это позволяет избежать потери корней. Каким конкретно числом должно быть новое основание логарифмов всегда можно понять, проанализировав данное уравнение.
Так в рассмотренном выше примере, подходящим новым основанием логарифмов является число 2. Это следует из того, что все входящие в уравнения основания логарифмов имеют вид: 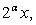 где α — целое число.
где α — целое число.
Далее, с учетом этого замечания оформим решение уравнения из примера 6 как схему равносильных переходов.
Еще раз следует отметить, что решение любого уравнения должно осуществляться не механически, а сознательно, с пониманием сущности всех преобразований, с обязательным анализом возможностей появления посторонних корней и потери корней. Если такой анализ непосредственно «вплетен» в ход решения, то наиболее действенно оформлять это решение схемой равносильных переходов. Хотя это и приводит, порой, к весьма громоздким записям. Громоздкости при записи решения уравнения в виде схемы равносильных переходов можно избежать следующим приемом: начать решение уравнения с нахождения области определения и затем при проведении решения соблюдать не «равносильность вообще», а «равносильность на области определения». Оформим решение уравнения из примера 6 с учетом этого приема.
Область определения этого уравнения (множество М):
Далее имеем:
Оформим также в виде равносильных переходов решения уравнений из следующих примеров. Эти уравнения (весьма распространенные в заданиях ЕГЭ, группа С), содержащие логарифмы, у которых и основания, и логарифмируемые выражения — выражения с переменной.
Пример 8.6.
Решение
Область определения этого уравнения (множество М):
Далее, имеем:
Ответ:  2.
2.
Пример 8.7.
Ответ:  а) Ø; б) 1.
а) Ø; б) 1.
Рассмотрим далее несколько примеров решения логарифмических неравенств.
Пример 8.8.
Решение
Таким образом, решение данного неравенства: 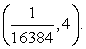
Пример 8.9.
Решение
Таким образом, решение исходного неравенства: 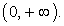
Пример 8.10.
Решение
Таким образом, решение исходного неравенства: 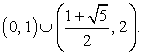
И, наконец, рассмотрим примеры решения логарифмических уравнений с параметром.
Пример 8.11.
Решение
Так же, как и в предыдущем примере, будем строго соблюдать требования равносильности преобразований. Тогда имеем:
Найдем х из уравнения 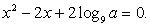 Имеем:
Имеем: 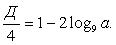 Т.е., условие существования корней этого квадратного уравнения:
Т.е., условие существования корней этого квадратного уравнения: 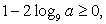 или
или 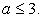
Условие существования корней исходного логарифмического уравнения задаются, таким образом, следующей системой неравенств:
Таким образом, исходное уравнение имеет единственный корень x = 1, если a = 3, имеет два корня вида 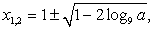 если
если 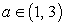 и не имеет корней, если
и не имеет корней, если 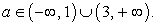
Ответ:  Если a = 3, то единственный корень x = 1, если
Если a = 3, то единственный корень x = 1, если 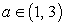 — два корня вида
— два корня вида 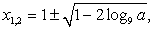 если
если 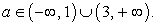 — нет корней.
— нет корней.
Пример 8.12.
Решение
Прежде всего выясним условие существования корней уравнения. Имеем систему:
Далее перейдем к одному и тому же основанию логарифмов и решим уравнение:
Таким образом, исходное уравнение имеет единственный корень вида 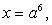 если
если 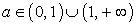 и не имеет корней, если
и не имеет корней, если 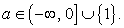
Ответ:  если
если 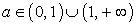 , то единственный корень
, то единственный корень 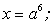 , если
, если 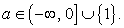 — корней нет.
— корней нет.
Комментарий. Для решения показательного уравнения его нужно свести к простейшему уравнению вида 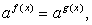 откуда следует, что
откуда следует, что 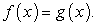 Иногда такое преобразование можно провести непосредственно, в других случаях требуется предварительно сделать замену переменной.
Иногда такое преобразование можно провести непосредственно, в других случаях требуется предварительно сделать замену переменной.
Пример 8.13.
Решение
Представим обе части равенства в виде степеней с основанием 2:
Пример 8.14.
Решение
Пример 8.15.
Решение
Преобразуем левую часть: 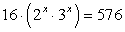 и разделим обе части на 16:
и разделим обе части на 16: 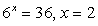
Ответ:  2.
2.
Пример 8.16.
Решение
Запишем уравнение в виде: 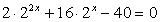 и сделаем замену:
и сделаем замену: 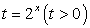 .
.
Ответ:  1.
1.
Пример 8.17.
Решение
Если записать левую часть так: 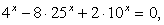 то можно заметить, что основания степеней (числа 4, 10, 25) образуют геометрическую прогрессию. В этом случае можно разделить обе части равенства, например, на
то можно заметить, что основания степеней (числа 4, 10, 25) образуют геометрическую прогрессию. В этом случае можно разделить обе части равенства, например, на 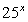 (поскольку ни при каком х это выражение не равно нулю) и получить уравнение
(поскольку ни при каком х это выражение не равно нулю) и получить уравнение 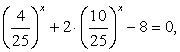 или
или 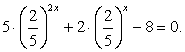 Замена
Замена 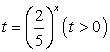 приводит к уравнению
приводит к уравнению 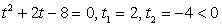 — посторонний корень.
— посторонний корень.
Пример 8.18.
Решение
Разложим левую часть на множители: 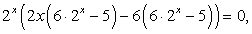
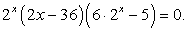 Первый множитель никогда не равен нулю, поэтому ответом будут корни уравнений:
Первый множитель никогда не равен нулю, поэтому ответом будут корни уравнений:
Случай 1: 2х - 6 = 0, х = 3.
Пример 8.19.
Решение
Заметим, что первое подмодульное выражение положительно при любом х, то есть его модуль равен подмодульному выражению. Рассмотрим две возможности для знака второго подмодульного выражения:
Случай 2: 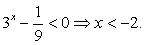 При этом
При этом 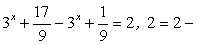 — тождество, следовательно, любое значение x < -2 является решением уравнения.
— тождество, следовательно, любое значение x < -2 является решением уравнения.
Пример 8.20.
Решение
При решении этого уравнения важно не забыть, что равенство будет верным не только в случае, когда показатель степени равен 0, но и тогда, когда основание степени в левой части равно 1, так как при возведении 1 в любую степень мы получим 1. Кроме того, ОДЗ определяется условием: х - 5 ≠ 0, то есть х ≠ 5.
Комментарий. Решение показательных неравенств сводится к решению простейших неравенств:
Важно помнить при этом, что при a > 1 можно перейти к неравенству, связывающему показатели степеней, знак которого совпадает со знаком исходного неравенства; при 0 < a < 1 показатели будут связаны неравенством противоположного знака.
Пример 8.21.
Решение
Представим обе части неравенства как степени с основанием 2:
Пример 8.22.
Решение
После замены 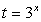 решим систему неравенств:
решим систему неравенств:
Поскольку знаменатель дроби в правой части второго неравенства при t > 0 положителен, можно умножить на него обе части неравенства, превратив его в квадратное:
Сделаем обратную замену: 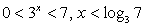 (левая часть неравенства верна при любом х).
(левая часть неравенства верна при любом х).
Пример 8.23.
Решение
Пример 8.24.
Решение
Перенесем все слагаемые в левую часть и разложим ее на множители:
Найдем корни левой части неравенства.
Решим неравенство методом интервалов:
Итак, 0 < x < 2.
Ответ:  (0; 2).
(0; 2).
Пример 8.25.
Решение
Запишем неравенство в виде: 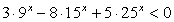 и разделим обе его части на
и разделим обе его части на 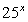 (при делении на положительное число знак неравенства не изменится):
(при делении на положительное число знак неравенства не изменится):
Поскольку основание степени меньше 1, при переходе к показателям знак неравенства меняется: -1 < x < 0.
Ответ:  (- 1; 0).
(- 1; 0).
Пример 8.26.
Решение
Замена 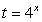 превращает неравенство в иррациональное:
превращает неравенство в иррациональное:
Комментарий. В логарифмических уравнениях, в отличие от показательных, нужно внимательно следить за тем, чтобы не включить в ответ посторонние корни. Их появление связано с дополнительными ограничениями на знак логарифмируемых выражений и оснований логарифмов.
Логарифмическое уравнение можно привести к одному или нескольким простейшим следующих видов.
-
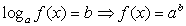 . При этом f (x) принимает только положительные значения, поэтому посторонние корни не появляются (если не было ограничений ранее).
. При этом f (x) принимает только положительные значения, поэтому посторонние корни не появляются (если не было ограничений ранее).
Пример 8.27.
Решение
Определим ОДЗ: 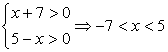 и перейдем во втором логарифме к основанию 4:
и перейдем во втором логарифме к основанию 4: 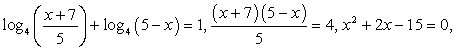
x1 = -5, x2 = 3 (оба входят в ОДЗ).
Ответ:  - 5; 3.
- 5; 3.
Пример 8.28.
Решение
Представим 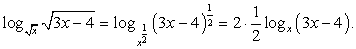 Тогда уравнение можно записать так:
Тогда уравнение можно записать так:
x1 = 1 — не входит в ОДЗ, x2 = 5 — входит в ОДЗ.
Ответ:  5.
5.
Пример 8.29.
Решение
Перейдем в обоих логарифмах к основанию 10:
Ответ:  2.
2.
Пример 8.30.
Решение
Обратите внимание на то, что логарифмируемое выражение представляет собой полный квадрат, поэтому оно положительно при всех х, кроме х = 3. Условие на подкоренное выражение задается в виде строгого неравенства, так как знаменатель не должен равняться нулю.
При выполнении этих условий уравнение можно записать так:
Ответ:  -5.
-5.
Пример 8.31.
Решение
ОДЗ: x > 1 (при этом 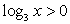 и
и 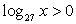 , то есть положительными являются аргументы внешних логарифмов).
, то есть положительными являются аргументы внешних логарифмов).
Перейдем во всех логарифмах к основанию 3:
Ответ:  27.
27.
Комментарий. В логарифмических уравнениях часто полезно применять замену переменной.
Пример 8.32.
Решение
Сделаем обратную замену.
Пример 8.33.
Решение
Представим 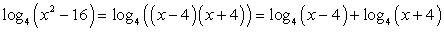 и введем новые переменные:
и введем новые переменные: 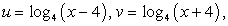 для которых имеем уравнение:
для которых имеем уравнение:
Приравняем к нулю каждый множитель.
Ответ:  8.
8.
Комментарий. Нередко в уравнение входят одновременно логарифмические и показательные функции. Рассмотрим такие комбинированные задания.
Пример 8.34.
Решение
Представим: 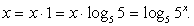 Тогда уравнение примет вид:
Тогда уравнение примет вид:
Сделаем замену: 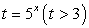 и решим уравнение для t:
и решим уравнение для t:
Ответ:  1.
1.
Пример 8.35.
Решение
ОДЗ: x > 0.
При выполнении этого условия обе части равенства положительны, поэтому их можно логарифмировать. Прологарифмируем левую и правую части по основанию 10:
Замена t = lg x приводит к уравнению 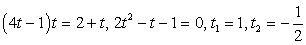
Случай 1: lg x = 1, x = 10.
Пример 8.36.
Решение
Прологарифмируем обе части по основанию 9:
x2 - 3х - 10 = 0, x1 = 5, x2 = -2 — не входит в ОДЗ.
Ответ:  5.
5.
Комментарий. При решении показательно-логарифмических систем применяются как обычные методы решения систем (подстановка, замена переменных), так и приемы решения соответствующих уравнений. Если в системе присутствуют логарифмы, не забудьте об ограничениях на допустимые значения неизвестных. Если получившиеся неравенства трудны для решения (например, неравенства с двумя переменными), можно ограничиться подстановкой в них найденных решений.
Пример 8.37.
Решение
ОДЗ: x > 0, y > 0.
Из первого уравнения можно сделать подстановку:
Находим соответствующие значения у: y1 = 4 - 1 = 3, y2 = 4 - 3 = 1. Все найденные решения входят в ОДЗ.
Ответ:  (1; 3), (3; 1).
(1; 3), (3; 1).
Пример 8.38.
Решение
ОДЗ: x > 0, y > 0, x ≠ 1, y ≠ 1.
Пусть 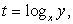 , тогда
, тогда 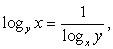 и из первого уравнения получаем:
и из первого уравнения получаем:
Случай 1: 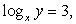 следовательно, у = х3
. Подставим во второе уравнение: x4
= 81, с учетом ОДЗ х = 3, у = 33
= 27.
следовательно, у = х3
. Подставим во второе уравнение: x4
= 81, с учетом ОДЗ х = 3, у = 33
= 27.
Ответ:  (3; 27), (27; 3).
(3; 27), (27; 3).
Пример 3.39.
Решение
Сделаем замену: 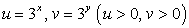 и получим систему:
и получим систему:
Получено однородное уравнение. Разделим обе части на 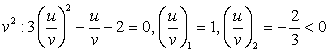 — постороннее решение, так это отношение может быть только положительным.
— постороннее решение, так это отношение может быть только положительным.
Итак, 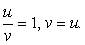 Подставим этот результат в первое уравнение системы для u и v:
Подставим этот результат в первое уравнение системы для u и v:
Единственный положительный корень этого уравнения — 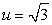 . Тогда
. Тогда 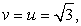 и после обратной замены получаем:
и после обратной замены получаем: 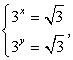 следовательно,
следовательно, 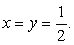
Пример 3.40.
Решение
ОДЗ: x > 0, y > 0.
Перейдем во всех логарифмах к основанию 3:
Разделим левую и правую части первого уравнения на соответствующие части второго:
Второе решение отрицательно, и является посторонним, так как х и у одного знака, следовательно, их отношение положительно.
Получена подстановка: х = 4у. Тогда из второго уравнения последней системы 4у3 = 1,
у = 1, х = 4.
Ответ:  (4; 1).
(4; 1).
Пример 8.41.
Решение
ОДЗ: x > 0, y > 0.
При выполнении этих условий прологарифмируем обе части каждого уравнения по основанию 2: 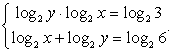
Представим 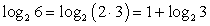 и сделаем замену:
и сделаем замену: 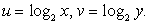 Для новых неизвестных решим систему:
Для новых неизвестных решим систему:
Заметим, что корни квадратного уравнения для и легко можно найти по теореме Виета.
Обратная замена:
Ответ:  (2; 3), (3; 2).
(2; 3), (3; 2).
Комментарий. Простейшее логарифмическое неравенство 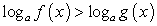 сводится к одной из двух систем неравенств.
сводится к одной из двух систем неравенств.
Пример 3.42.
Решение
Используя свойства логарифмов, преобразуем левую часть: 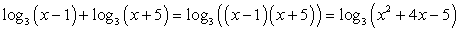 и решим систему неравенств:
и решим систему неравенств:
Обращаем ваше внимание на то, что положительным должно быть каждое логарифмируемое выражение, а не только их произведение.
Ответ:  (1; 3).
(1; 3).
Пример 8.43.
Решение
Поскольку 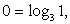 решаем неравенство
решаем неравенство 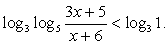 Оно равносильно системе:
Оно равносильно системе:
Заметим, что первое неравенство можно не решать, так как оно заведомо будет верным для всех решений второго неравенства. Тогда:
Комментарий. Если основание логарифма переменно и может принимать значения как меньшие, так и большие 1, нужно рассмотреть эти ситуации отдельно, так как в первом случае знак неравенства не меняется при переходе к аргументам, а во втором — меняется на обратный.
Пример 8.44.
Решение
Запишем неравенство в виде:
(учитываем, что x > 0, поэтому 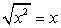 ).
).
Пример 8.45.
Решение
Пусть 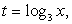 тогда
тогда 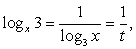 и для t получаем неравенство:
и для t получаем неравенство: 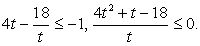 Не забудьте, что в дробно-рациональном неравенстве важен знак не только числителя, но и знаменателя дроби, и решать его лучше всего методом интервалов (самая распространенная ошибка на этом этапе решения — «отбрасывание» знаменателя). Корни числителя:
Не забудьте, что в дробно-рациональном неравенстве важен знак не только числителя, но и знаменателя дроби, и решать его лучше всего методом интервалов (самая распространенная ошибка на этом этапе решения — «отбрасывание» знаменателя). Корни числителя: 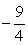 и 2, корень знаменателя — 0, и знак дроби распределяется на интервалах так:
и 2, корень знаменателя — 0, и знак дроби распределяется на интервалах так:
Следовательно, 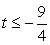 или 0 < t ≤ 2 (корень знаменателя, разумеется, в ответ не входит).
или 0 < t ≤ 2 (корень знаменателя, разумеется, в ответ не входит).
Пример 8.46.
Сделаем замену: 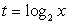 и решим для t иррациональное неравенство
и решим для t иррациональное неравенство 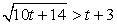 .
.
Обратная замена:
Пример 8.47.
Решение
Определим ОДЗ: 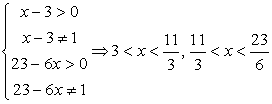 и перейдем в обоих логарифмах к основанию 2:
и перейдем в обоих логарифмах к основанию 2:
Найдем корни числителя и знаменателя.
Случай 1:
Случай 2:
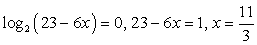 (само это значение тоже не входит в ОДЗ, но слева и справа от него определены все функции, присутствующие в неравенстве, и один из множителей знаменателя в этой точке меняет знак).
(само это значение тоже не входит в ОДЗ, но слева и справа от него определены все функции, присутствующие в неравенстве, и один из множителей знаменателя в этой точке меняет знак).
Итак, в рамках ОДЗ дробь меняет знак трижды: в точках 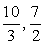 и
и 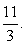 Расставим знаки на интервалах. При
Расставим знаки на интервалах. При 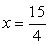 (точка, расположенная на самом правом интервале) х - 3 = 0,75 < 1, 23 - 6x = 0,5 < 1, -6x2
+ 41x - 69 = 0,375 < 1, поэтому все три логарифма, входящие в последнюю форму неравенства, отрицательны; соответственно, отрицательна и сама дробь.
(точка, расположенная на самом правом интервале) х - 3 = 0,75 < 1, 23 - 6x = 0,5 < 1, -6x2
+ 41x - 69 = 0,375 < 1, поэтому все три логарифма, входящие в последнюю форму неравенства, отрицательны; соответственно, отрицательна и сама дробь.
Пример 8.48.
Решение
Превратим простейшее неравенство 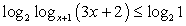 в систему:
в систему:
и перейдем к любому постоянному основанию (например, 2):
Решим второе и третье неравенства методом интервалов.
Случай 2: 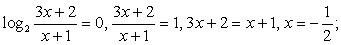 корень знаменателя (х = 0) тот же, что в предыдущем неравенстве.
корень знаменателя (х = 0) тот же, что в предыдущем неравенстве.
Окончательным решением будет пересечение полученных промежутков: 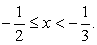
Пример 8.49.
Решение
Тогда:
Решим полученное неравенство методом интервалов.
Случай 1:
Случай 2:
Расставим знаки (при х = 10, то есть на самом правом из полученных промежутков, числитель дроби отрицателен, а знаменатель положителен, то есть вся дробь отрицательна).
Пример 8.50.
Решение
Найдем ОДЗ:
Перейдем к основанию 3:
Применим метод интервалов.
Отметим, что из всех изолированных точек, не входящих в ОДЗ, только х = -1 не является корнем числителя или знаменателя; соответственно в этой точке знак дроби не меняется.
Расставим знаки, учитывая, что на самом правом интервале все логарифмы, входящие в левую часть неравенства, положительны:
Ответ:  (- 7; - 6) U [ - 3; - 2) U (0; 2].
(- 7; - 6) U [ - 3; - 2) U (0; 2].
Комментарий. При решении подобных неравенств применяются те же приемы, что и при решении уравнений аналогичного типа (замены, логарифмирование, потенцирование). Как всегда, внимательно следите за ограничениями на ОДЗ.
Пример 3.51.
Решение
Представим 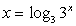 , сделаем замену
, сделаем замену 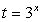 и решим для t систему неравенств с учетом ОДЗ:
и решим для t систему неравенств с учетом ОДЗ:
Пример 3.52.
Решение
Если прологарифмировать обе части неравенства по любому основанию, большему 1, знак неравенства не изменится (учитываем, что в области допустимых значений обе части положительны). Логарифмируем по основанию 10:
Пример 8.53.
Решение
Вновь перед нами в левой части выражение вида 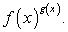 Наиболее удобный прием для упрощения — логарифмирование. Прологарифмируем обе части по основанию 4 и составим систему неравенств с учетом ОДЗ:
Наиболее удобный прием для упрощения — логарифмирование. Прологарифмируем обе части по основанию 4 и составим систему неравенств с учетом ОДЗ:
Решим последнее неравенство методом интервалов.
Случай 2: 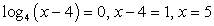 — точка лежит внутри ОДЗ, знак дроби в ней меняется.
— точка лежит внутри ОДЗ, знак дроби в ней меняется.
При достаточно больших значениях х аргумент логарифма, стоящего в числителе, меньше 1, то есть числитель дроби отрицателен, а знаменатель положителен. С учетом этого расставим знаки на интервалах:
Таким образом, 4 < x < 5 или х ≥ 8.
Ответ:  (4; 5) U [8; +∞).
(4; 5) U [8; +∞).
Пример 8.54.
Решение
Задаем ОДЗ и логарифмируем обе части по основанию 3:
Последнее неравенство решаем методом интервалов.
Случай 1: 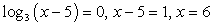 — сама эта точка в ОДЗ не входит, но знак первого множителя в ней меняется.
— сама эта точка в ОДЗ не входит, но знак первого множителя в ней меняется.
Расставим знаки на интервалах (при x > 11 левая часть положительна):
Ответ:  (5; 6) U [8; +∞).
(5; 6) U [8; +∞).
Пример 8.55.
Решение
Воспользуемся одним из свойств логарифмов: 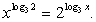
Неравенство сразу резко упрощается:
Ответ:  (0; 27].
(0; 27].
Пример 8.56.
Решение
Упростим второй множитель левой части: 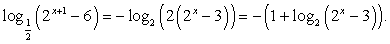
Этот результат позволяет сделать замену 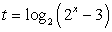 и решать неравенство: -t(t + 1) ≤ -2, t(t + 1) ≥ 2, t2
+ t - 2 ≥ 0, t ≤ -2 или t ≥ 1. Сделаем обратную замену.
и решать неравенство: -t(t + 1) ≤ -2, t(t + 1) ≥ 2, t2
+ t - 2 ≥ 0, t ≤ -2 или t ≥ 1. Сделаем обратную замену.
Пример 8.57.
Решение
Обратная замена.
Случай 1:
Случай 2:
Пример 8.58.
Решение
Учтем ОДЗ: x > 0, x ≠ 1 и прологарифмируем обе части по основанию 2:
Ответ:  (1; 4] U [8; +∞).
(1; 4] U [8; +∞).
Пример 8.59.
Решение
ОДЗ: x > 0, x ≠ 6 (подмодульное выражение не должно равняться нулю). Прологарифмируем обе части по основанию 2: 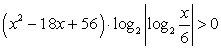 и решим полученное неравенство методом интервалов.
и решим полученное неравенство методом интервалов.
Случай 1: x2 - 18х + 56 = 0, x1 = 4, x2 = 14.
Расставим знаки на интервалах, учитывая, что при x > 14 левая часть неравенства положительна, а при х = 6 ни один из множителей не меняет знак:
Ответ:  (0; 3) U (4; 6) U (6; 12) U (14; +∞).
(0; 3) U (4; 6) U (6; 12) U (14; +∞).
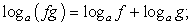
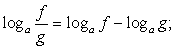
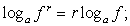
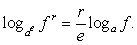
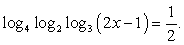
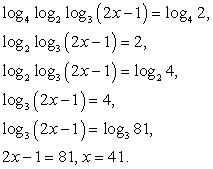
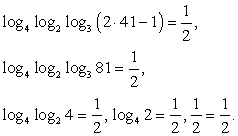
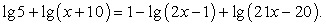
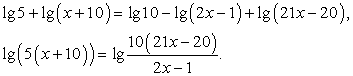
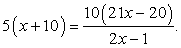
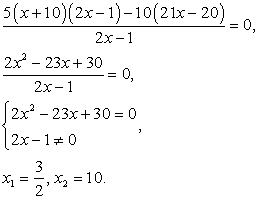
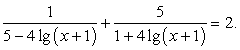
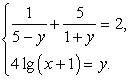
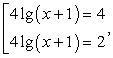 т.е.
т.е. 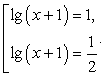
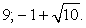
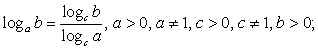
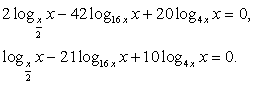
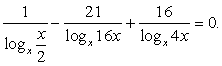
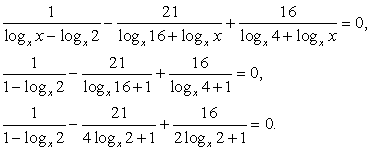
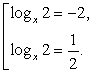
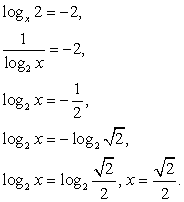
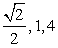
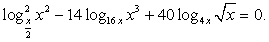
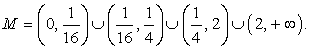
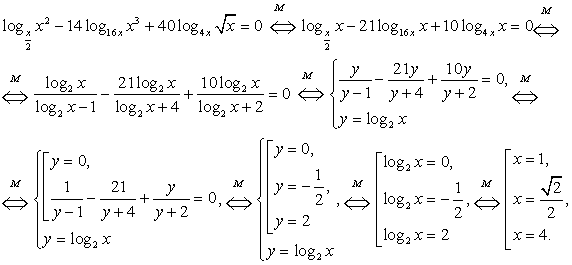
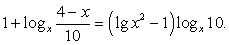
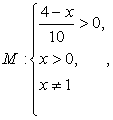 т.е.
т.е. 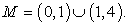
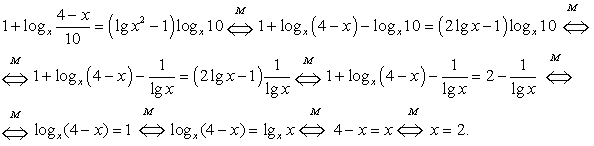
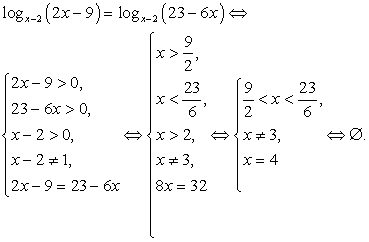
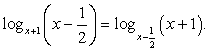
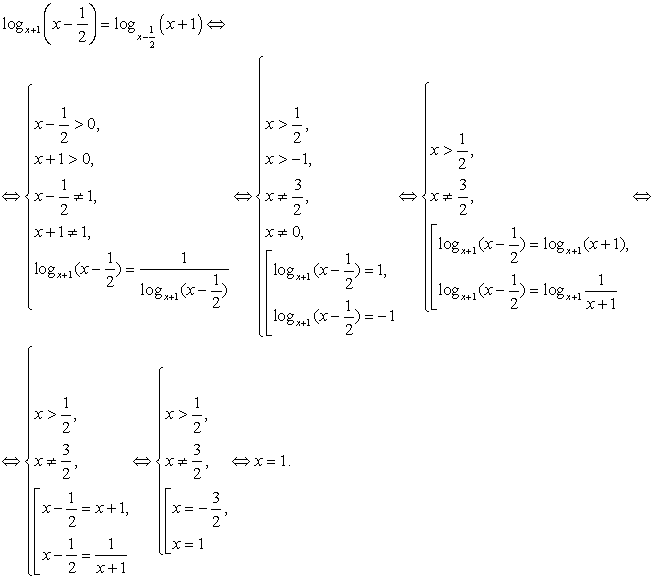
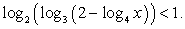
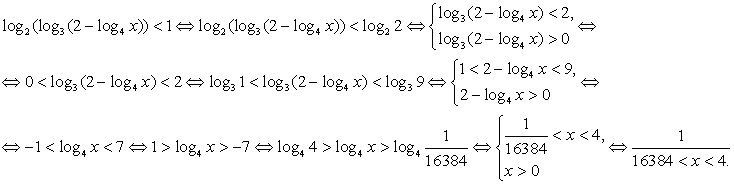
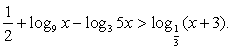
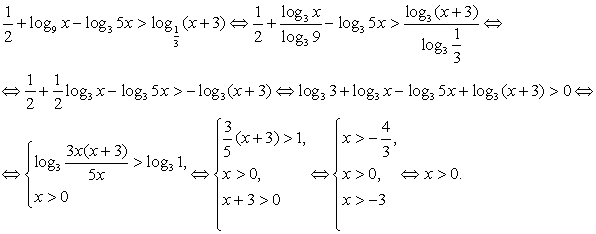
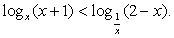
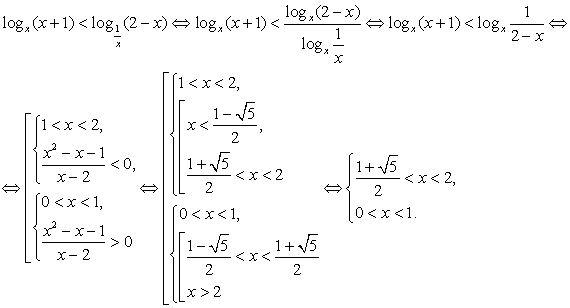
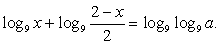
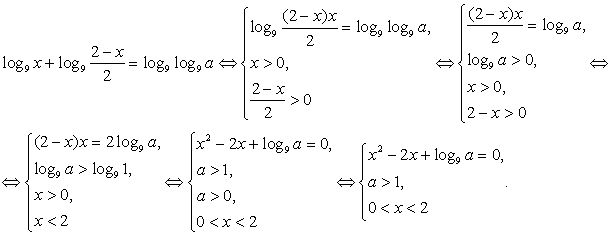
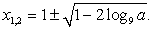
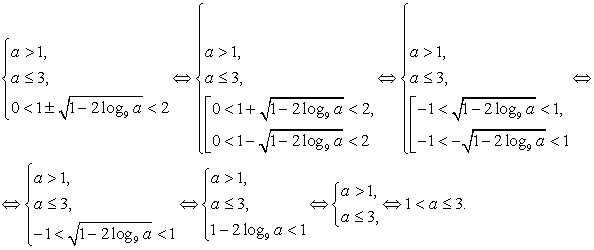
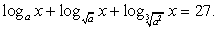
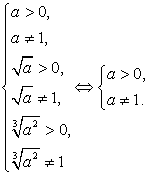
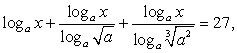
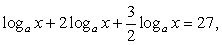
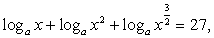
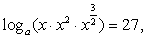
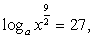
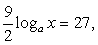
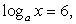
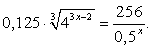
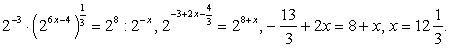
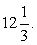
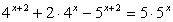
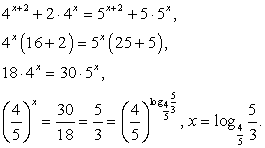
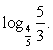
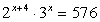
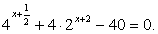
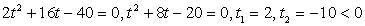 — посторонний корень.
— посторонний корень.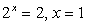 .
.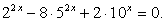
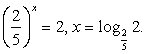
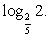
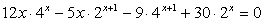 .
.
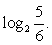
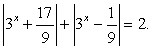
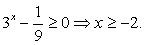 Тогда
Тогда 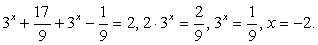
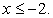
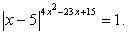
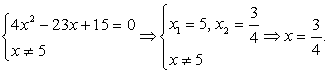
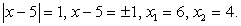
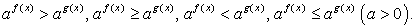
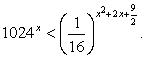
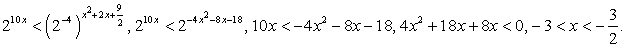
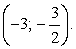
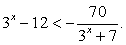
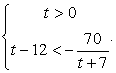
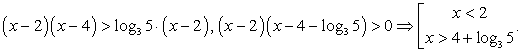
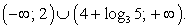
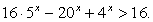
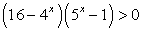 .
.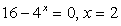 .
.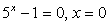 .
.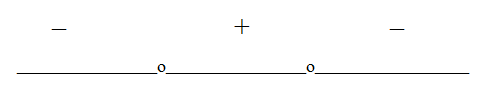
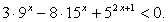
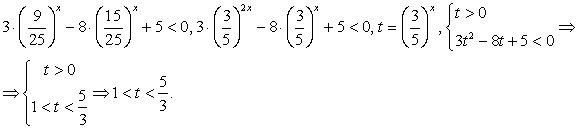
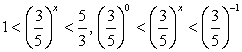 .
.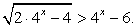
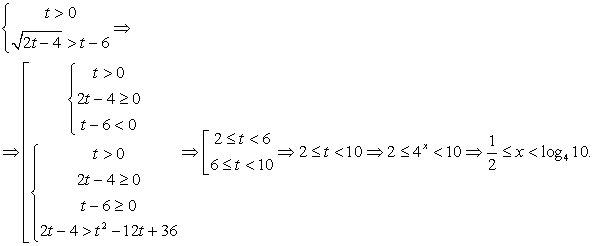
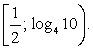
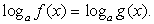 Такое уравнение можно свести к системе:
Такое уравнение можно свести к системе: 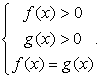
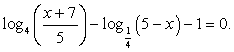
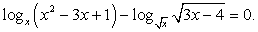
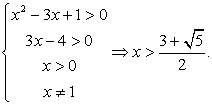
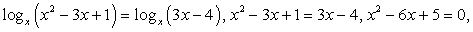
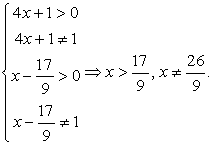
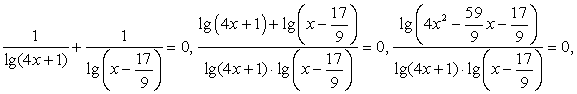
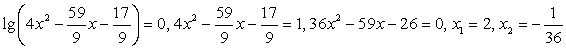 — не входит в ОДЗ.
— не входит в ОДЗ.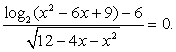
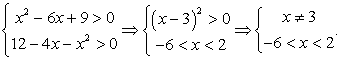
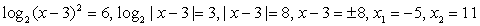 — не входит в ОДЗ.
— не входит в ОДЗ.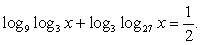
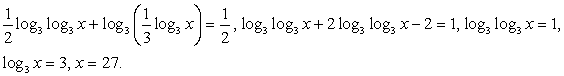
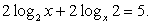
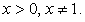
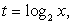 тогда:
тогда: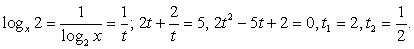
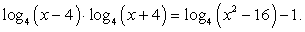
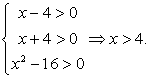
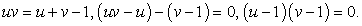
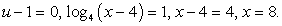
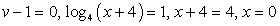 — не входит в ОДЗ.
— не входит в ОДЗ.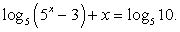
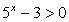
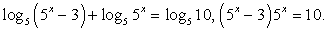
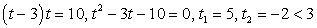 — посторонний корень.
— посторонний корень.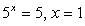 .
.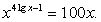
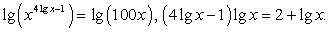
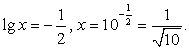
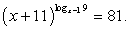
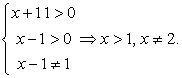
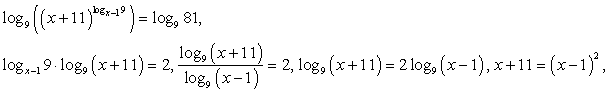
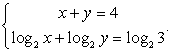
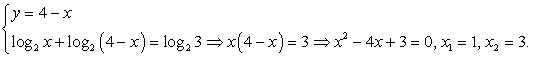
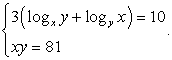
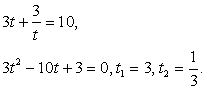
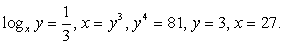
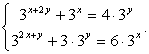
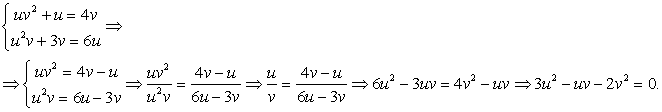
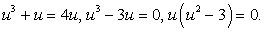
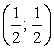
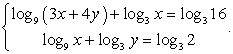
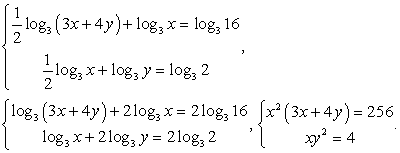
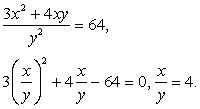 .
.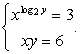
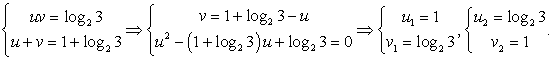
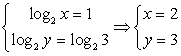 ;
;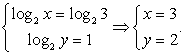
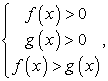 если a > 1.
если a > 1.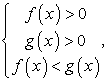 если 0 < a < 1.
если 0 < a < 1.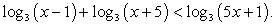
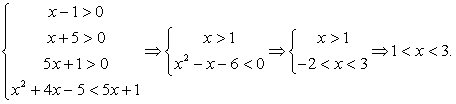
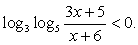
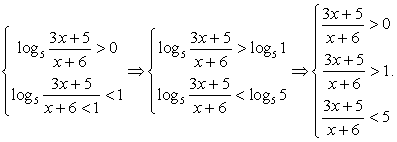
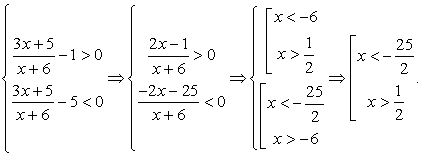
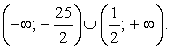
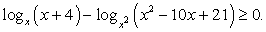
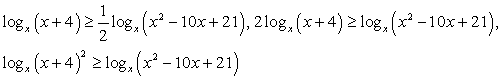
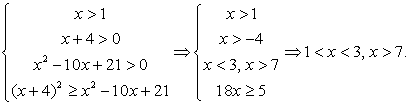
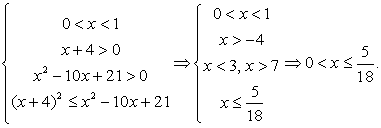
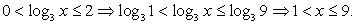
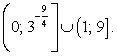
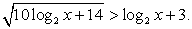
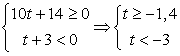 — решений нет.
— решений нет.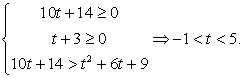
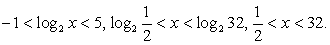
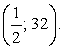
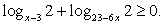
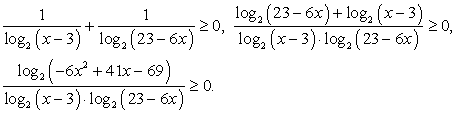
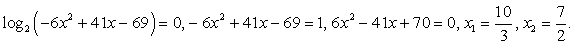
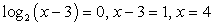 — не входит в ОДЗ.
— не входит в ОДЗ.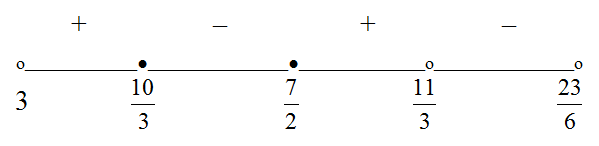
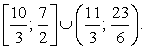
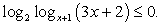
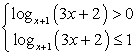
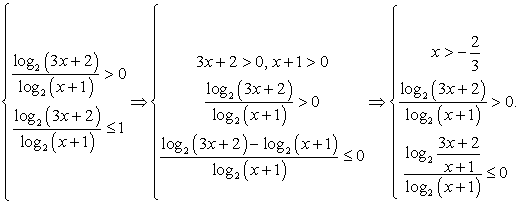
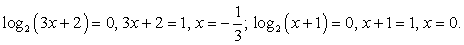
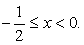
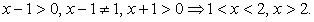
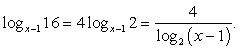
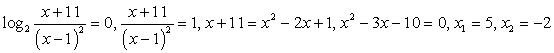 — не входит в ОДЗ.
— не входит в ОДЗ.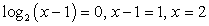 — точка, лежащая внутри ОДЗ.
— точка, лежащая внутри ОДЗ.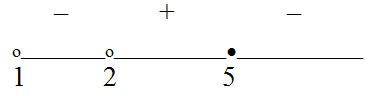
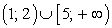 .
.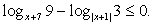
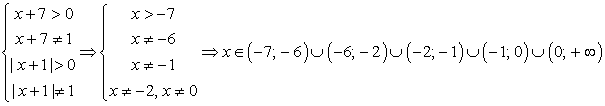 .
.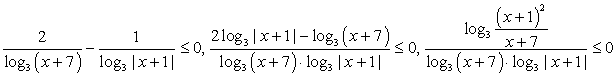
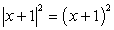 ).
).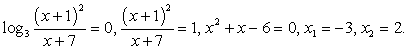
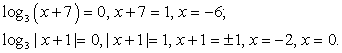
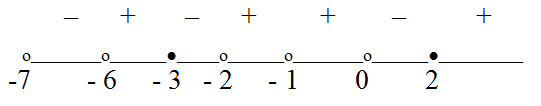
 .
.
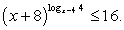
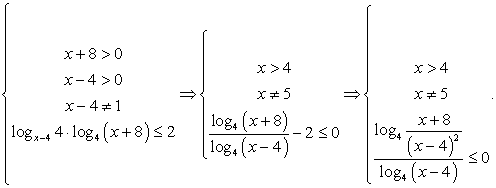
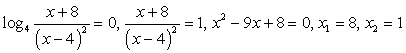 — не входит в ОДЗ.
— не входит в ОДЗ.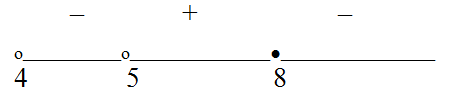
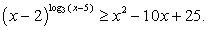
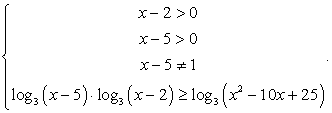
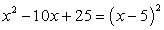 . Тогда:
. Тогда: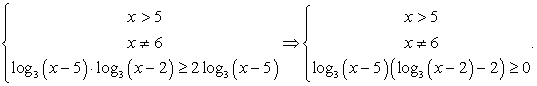
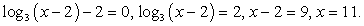
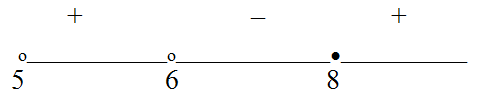
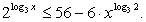
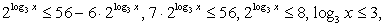 и, с учетом ОДЗ, 0 < x ≤ 27.
и, с учетом ОДЗ, 0 < x ≤ 27.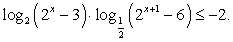
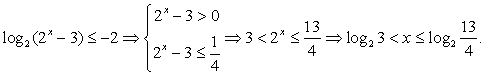
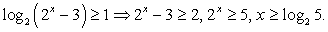
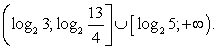
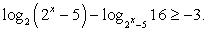
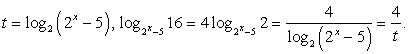
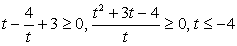 или
или 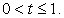
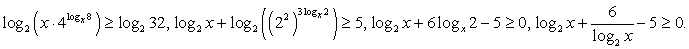
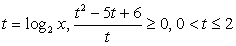 или
или