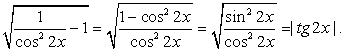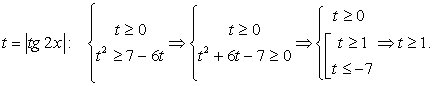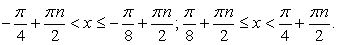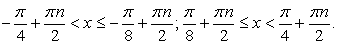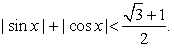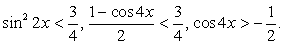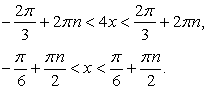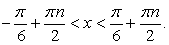Комментарий. Устойчивым является заблуждение абитуриентов о том, что при решении тригонометрических уравнений не нужна проверка. Это — далеко не всегда.
При решении тригонометрических уравнений проверка найденных решений необходима, если:
1) в процессе решения применялись алгебраические преобразования, которые могли привести к расширению области определения уравнения (например, сокращение дробей);
2) в процессе решения применялись тригонометрические преобразования, которые могли привести к расширению области определения уравнения (речь идет о применении тригонометрических формул, левая и правая части которых имеют различные области определения, например:
3) в процессе решения применялось возведение обеих частей уравнения в одну и ту же степень.
Каждая из указанных причин может привести к появлению посторонних корней. Заметим, что применение формул из п. 2 «справа налево», напротив, может привести к потере корней, в силу сужения области определения.
Решение тригонометрических уравнений в большинстве случаев проводится либо с помощью замены переменной, либо разложения на множители, но и тот, и другой способ применяется в разных вариантах в зависимости от вида конкретного уравнения. Поэтому в данном разделе вам предлагается более подробная классификация типов тригонометрических уравнений и методов их решения.
Пример 7.1.
Решение
Обе части уравнения легко представляются как выражение, зависящее только от tgx:
Далее, заменой tgx = y, тригонометрическое уравнение рационализуется:
Однако можно заметить, что значения 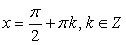 также удовлетворяют исходному уравнению. Это потерянные корни. В чем причина?! В основе преобразований формулы, сужающие область определения:
также удовлетворяют исходному уравнению. Это потерянные корни. В чем причина?! В основе преобразований формулы, сужающие область определения: 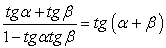 .
.
Комментарий. Еще раз настойчиво предостерегаем от применения приемов решения уравнений, ведущих к сужению области определения и возможной потере корней.
Пример 7.2.
Решение
Перераспределим компоненты уравнения: 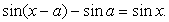
Далее, в левой части воспользуемся формулой: 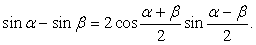
Теперь представим sin x как синус двойного аргумента:
Перенесем все компоненты уравнения в одну часть и вынесем общий множитель за скобки:
Вновь воспользуемся формулой разности синусов:
Последнее уравнение равносильно совокупности:
Таким образом, уравнение имеет два семейства корней: 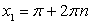 и
и 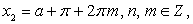 , если
, если 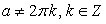 и бесконечно много корней:
и бесконечно много корней: 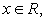 если
если 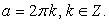
Рассмотрим также примеры решения комбинированных уравнений, т.е. уравнений, в которых над переменной, в той или иной комбинации производятся иррациональные, показательно-степенные, логарифмические и тригонометрические операции. Такого рода задания вызывают у абитуриентов определенные трудности. В основе этих трудностей, как правило, лежит некая негативная психологическая установка. Абитуриент как бы говорит себе: «Таких уравнений я в школе не решал; что-то слишком много всего накручено; это мне не по силам». В связи с этим дадим два совета.
Совет первый. По внешнему виду задания нельзя судить о его простоте или трудности; трудность — это характеристика не задания, а действенности Ваших знаний и умений. Начинайте решать, пробуйте, пытайтесь, несмотря на то, что задание кажется вам «страшным» и недоступным.
Совет второй. Решайте комбинированное уравнение как бы по действиям, отграничивая иррациональную часть решения от логарифмической, логарифмическую от тригонометрической и т.п. Осуществить это можно введением новых переменных. В конце решения осуществляйте тем или иным образом проверку корней.
Пример 7.3.
Решить уравнение.
Решение
Пусть 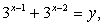 тогда
тогда 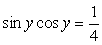 . Далее решаем уже не комбинированное, а тригонометрическое уравнение. Воспользуемся формулой синуса двойного аргумента:
. Далее решаем уже не комбинированное, а тригонометрическое уравнение. Воспользуемся формулой синуса двойного аргумента:
«Тригонометрическая часть» решения завершена; далее необходимо решить показательное уравнение с параметром n:
Прежде всего, выясним, при всех ли n у данного уравнения существуют корни. Ясно, что, поскольку левая часть уравнения, как сумма степеней тройки, всегда положительна, то условие существования корней уравнения:
Решим это неравенство. Если n > 0, то 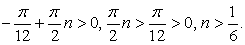 Очевидно, что полученная система
Очевидно, что полученная система 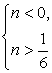 несовместна. Если n ≥ 0, то
несовместна. Если n ≥ 0, то 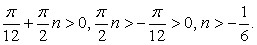
Система 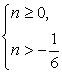 равносильна неравенству n ≥ 0.
равносильна неравенству n ≥ 0.
Таким образом, учитывая, что 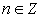 , получаем вывод: корни у данного уравнения существуют при значениях параметра n: n = 0, 1, 2, 3, … . Именно при этом условии решаем далее показательное уравнение.
, получаем вывод: корни у данного уравнения существуют при значениях параметра n: n = 0, 1, 2, 3, … . Именно при этом условии решаем далее показательное уравнение.
Преобразуем левую часть уравнения по свойствам степени:
Тогда имеем:
Таким образом, 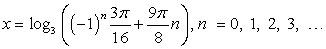 Это «семейство» логарифмов и составляет множество корней исходного комбинированного (показательно — тригонометрического) уравнения.
Это «семейство» логарифмов и составляет множество корней исходного комбинированного (показательно — тригонометрического) уравнения.
Пример 7.4.
Решение
Прежде всего, укажем область определения уравнения. Она задается условиями:
Пусть, теперь 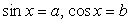 . Тогда, вместо комбинированного, имеем логарифмическое уравнение с двумя переменными а и b:
. Тогда, вместо комбинированного, имеем логарифмическое уравнение с двумя переменными а и b: 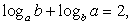 это уравнение преобразуется в уравнение:
это уравнение преобразуется в уравнение: 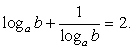 Далее, если положить, что
Далее, если положить, что 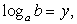 то имеем простое рациональное уравнение:
то имеем простое рациональное уравнение: 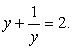 Его единственный корень — y = 1. Значит,
Его единственный корень — y = 1. Значит, 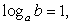 т.е.
т.е. 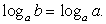
Отсюда b = a, т.е. 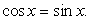 Корнями этого тригонометрического уравнения является семейство:
Корнями этого тригонометрического уравнения является семейство: 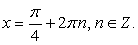 Нетрудно видеть, что оно удовлетворяет области определения исходного уравнения, а значит, и составляет множество его корней.
Нетрудно видеть, что оно удовлетворяет области определения исходного уравнения, а значит, и составляет множество его корней.
Пример 7.5.
Решение
Заметим, что решения всякого уравнения, следует начинать с пристального, внимательного взгляда, призванного увидеть в уравнении, неравенстве и т.п. что-нибудь интересное, особенное, какую-нибудь «изюминку», позволяющую применить при решении некий нестандартный прием. Эта «изюминка» не всегда есть, но проглядеть ее обидно. В данном уравнении маленькая «изюминка» есть: если в правой части уравнения мы воспользуемся (к сожалению часто забытым абитуриентами) свойством логарифма: 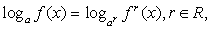 то сразу, как говорится, «убьем двух зайцев»: и избавимся от радикала, и перейдем к одному основанию логарифма.
то сразу, как говорится, «убьем двух зайцев»: и избавимся от радикала, и перейдем к одному основанию логарифма.
Итак, если r = 2, то 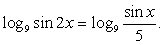 Далее, имеем тригонометрическое уравнение
Далее, имеем тригонометрическое уравнение 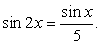 Воспользуемся формулой синуса двойного аргумента:
Воспользуемся формулой синуса двойного аргумента:
Решением первого уравнения совокупности является семейство: 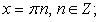 решением второго:
решением второго: 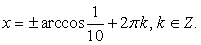
Необходимо провести проверку найденных корней. Для этого выпишем условия, задающие область определения исходного уравнения:
Ясно, что первое из найденных семейств — семейство посторонних корней, т.к. нарушено условие 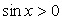 , а из второго семейства посторонними корнями являются корни вида:
, а из второго семейства посторонними корнями являются корни вида: 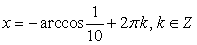 (т.к., в этом случае, хотя
(т.к., в этом случае, хотя 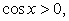 но
но 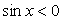 ).
).
Таким образом, корни исходного комбинированного уравнения:
Пример 7.6.
Решение
Внесем множитель два в левой части уравнения под логарифм в качестве показателя степени: 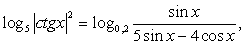 и перейдем к основанию логарифма пять в левой части уравнения:
и перейдем к основанию логарифма пять в левой части уравнения:
«Отбрасывая» логарифмы, получаем: 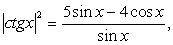 и далее, учитывая, что
и далее, учитывая, что 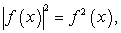 и переходя к разности дробей в левой части уравнения:
и переходя к разности дробей в левой части уравнения:
Это квадратное уравнение относительно ctgx, корни которого 1 и -5. Т.е. имеем совокупность: 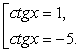
Решением первого уравнения совокупности является семейство: 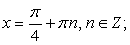 решением второго:
решением второго: 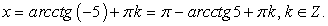 Здесь применено тождество:
Здесь применено тождество: 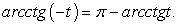
Далее необходимо провести проверку корней. В качестве способа проверки в данном случае, изберем непосредственную подстановку в исходное уравнение. При этом ясно, что речь идет о подстановке в исходное уравнение лишь одного значения принадлежащего данному семейству. Этого достаточно. Удобнее всего, взять значения n = 0 и х = -1. Но можно поступить еще проще: в равносильности совокупностей
мы не сомневаемся, а поэтому в исходное уравнение можно подставлять непосредственно каждое из получившихся значений ctg x.
В каждом случае изберем более удобный из описанных подходов.
Пусть 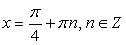 и n = 0, т.е.
и n = 0, т.е. 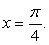 Тогда имеем:
Тогда имеем:
Таким образом, семейство: 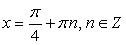 входит во множество корней исходного уравнения.
входит во множество корней исходного уравнения.
Пусть теперь ctg x = -5 (здесь реализуем второй подход, ибо осуществлять непосредственную подстановку x = -arcctg 5 неудобно). Тогда, поскольку 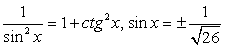 и
и 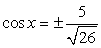 . Далее, т.к. ctgx < 0, то sin x и cos x должны быть разных знаков; имеем:
. Далее, т.к. ctgx < 0, то sin x и cos x должны быть разных знаков; имеем: 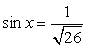 и
и 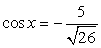 или
или 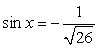 и
и 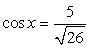 . В первом случае
. В первом случае 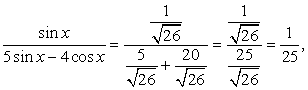 во втором случае
во втором случае 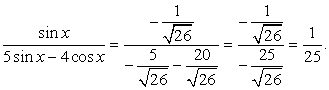
После подстановки в исходное уравнение имеем:
Таким образом, семейство 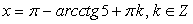 также входит во множество корней исходного уравнения.
также входит во множество корней исходного уравнения.
Пример 7.7.
Решение
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
Пример 7.8.
На первом этапе решения уравнения выясним область допустимых значений и выполним тождественные преобразования:
Решением уравнения является:
Комментарий. Данный прием решения тригонометрического уравнения принято называть методом разложения на множители.
Пример 7.9.
Используем в процессе решения формулы понижения степени, получим:
После приведения подобных слагаемых получаем уравнение, сводящееся к квадратному уравнению.
Данное уравнение приводится к квадратному с помощью замены переменной.
Пусть sin 2x = y, тогда:
Комментарий. Решение большого количества тригонометрических уравнений сводится к решению квадратных уравнений.
Пример 7.10.
Комментарий. Данный пример иллюстрирует возможность решения тригонометрических уравнений методом преобразования суммы тригонометрических функций в произведение.
Пример 7.11.
Во-первых, найдем область определения функции, выходящей в данной тригонометрическое уравнение:
Таким образом, областью определения данного уравнения является:
Во-вторых, решим данное уравнение. Для этого выполним следующие тождественные преобразования:
Комментарий. Решение тригонометрических уравнений в ряде случаев проводится преобразованием произведения тригонометрических функций в сумму.
Пример 7.12.
Решить тригонометрическое уравнение: 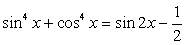 .
.
Решение
Используем в процессе решения формулы понижения степени:
Выполнив замену переменных, получим:
Комментарий. Решение тригонометрических уравнений с применением формул понижения степени.
Пример 7.13.
Решение
Используем далее основное тригонометрическое тождество:
Если 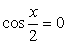 , то и
, то и 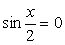 , что противоречит основному тригонометрическому тождеству, значит
, что противоречит основному тригонометрическому тождеству, значит 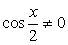 .
.
Разделим обе части на 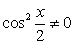 , получим:
, получим:
Комментарий. Данный пример показывает возможность решения тригонометрических уравнений как однородных уравнений. Однородное уравнение — это уравнение, в котором каждое слагаемое имеет одну и ту же степень:
где 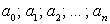 — действительные числа, n — показатель однородности.
— действительные числа, n — показатель однородности.
Пример 7.14.
Решение
Т.к. 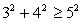 , следовательно, корни есть.
, следовательно, корни есть.
Разделим обе части уравнения на 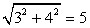 , получим:
, получим:
Т.к. 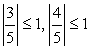 и
и 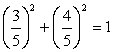 , то существует такой угол φ, что
, то существует такой угол φ, что 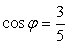 , а
, а 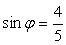 , тогда получим:
, тогда получим:
Комментарий. Рассмотренный прием решения тригонометрических уравнений называется методом введения вспомогательного аргумента.
Данный метод основан на следующем. Рассмотрим уравнение особого вида:
Случай 1. Если с = 0, то уравнение однородное.
Случай 2. Если с ≠ 0 и 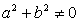 (то есть хотя бы одно из чисел a или b не равно 0), то разделим обе части уравнения на
(то есть хотя бы одно из чисел a или b не равно 0), то разделим обе части уравнения на 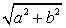 , получим:
, получим:
Т.к. 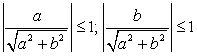 и
и 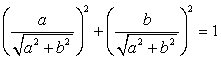 , то существует такой угол φ, что
, то существует такой угол φ, что 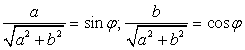 , тогда:
, тогда:
Пример 7.15.
Решение
Проверим выполнение неравенства: 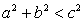 .
.
Очевидно, что 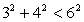 , следовательно, корней уравнение не имеет.
, следовательно, корней уравнение не имеет.
Пример 7.16.
Выполним преобразование уравнения, используя формулы «универсальная тригонометрическая подстановка»:
Получаем, что:
При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения 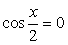 корнями данного уравнения.
корнями данного уравнения.
Проверка.
0 + 4 (-1) = 5 — не верно, значит, 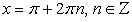 , не является корнями исходного уравнения.
, не является корнями исходного уравнения.
Комментарий. Данный пример показывает возможность решения тригонометрических уравнений с помощью универсальной тригонометрической подстановки.
Пример 7.17.
Решение
Далее возведем записанное равенство в квадрат и воспользуемся формулой «квадрат суммы»:
Получаем, что:
Разделим на cos x ≠ 0, получим:
Пример 7.18.
Решить уравнение: 2cos 2x - 4sin x + 1 = 0.
Решение
Используем формулу: 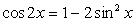 и сделаем замену
и сделаем замену 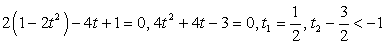 — посторонний корень (учитываем, что
— посторонний корень (учитываем, что 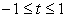 ).
).
Пример 7.19.
Решение
Применим следствие из основного тождества 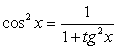 и сделаем замену t = tg x:
и сделаем замену t = tg x:
Найдем подбором корень t = -1 и разложим на множители левую часть полученного уравнения: (t + 1)(4t2
- t + 5) = 0. Дискриминант второго множителя отрицателен, следовательно, других корней уравнение не имеет. Обратная замена: 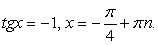
Комментарий. Приведенные приемы решения тригонометрических уравнений основаны на использовании основного тождества и формул для косинуса двойного угла.
Пример 7.20.
Поскольку 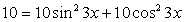 , a
, a 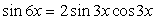 , уравнение можно записать в виде:
, уравнение можно записать в виде: 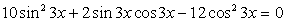 . Перед нами так называемое однородное уравнение, для всех слагаемых левой части которого сумма степеней sin 3x и cos 3x одинакова.
. Перед нами так называемое однородное уравнение, для всех слагаемых левой части которого сумма степеней sin 3x и cos 3x одинакова.
Проверкой можно убедиться, что cos 3x ≠ 0 для корней этого уравнения, поэтому можно разделить обе его части на 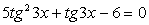 . Сделаем замену: t = tg 3x, тогда
. Сделаем замену: t = tg 3x, тогда 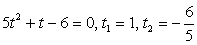 . Обратная замена:
. Обратная замена:
Пример 7.21.
Решить уравнение: 5sin 4x - 12cos 4x = 6,5.
Решение
Разделим обе части уравнения на 13:
Пусть  тогда
тогда 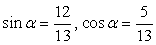 , и уравнение принимает вид:
, и уравнение принимает вид: 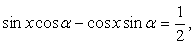 или
или 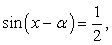 откуда
откуда 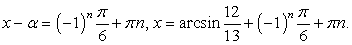
Пример 7.22.
Решить уравнение: sin 4x + sin 3x + cos 6x + cos 7x = 0.
Решение
Преобразуем в произведение сумму синусов и сумму косинусов:
Теперь запишем левую часть уравнения в виде:
Это равенство возможно в двух случаях.
Применим формулу приведения:
Тогда:
Это уравнение вновь сводится к двум простейшим:
Пример 7.23.
Решение
Применим к левой части метод дополнительного угла:
Выберем дополнительный угол так, чтобы получить в левой части формулу для косинуса разности:
Комментарий. Решение примера основано на формуле преобразования суммы тригонометрических функций в произведение.
Пример 7.24.
Решить уравнение: cos 9x + sin 4x sin 5x = 0.
Решение
Преобразуем произведение синусов в сумму: 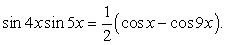
Тогда
Пример 7.25.
Решить уравнение: sin 6x + 3sin 4x cos 2x = 0.
Решение
Преобразуем произведение в сумму:
Воспользуемся формулой синуса тройного угла: 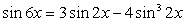 и сделаем замену: t = sin 2x. Решим уравнение для t:
и сделаем замену: t = sin 2x. Решим уравнение для t:
Обратная замена приводит к трем простейшим уравнениям.
Объединяя две последние группы корней, получим окончательный ответ.
Комментарий. Рассмотренный пример иллюстрирует использование преобразования произведения тригонометрических функций в сумму.
Пример 7.26.
Решить уравнение: sin 2x - 5 + 5sin x - 5cos x = 0.
Решение
Сделаем замену: t = sin x - cos x, тогда 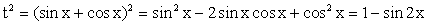 . Следовательно, sin 2x = 1 - t2
.
. Следовательно, sin 2x = 1 - t2
.
Подставим эти выражения в уравнение:
1 - t2 - 5 + 5t = 0, t2 - 5t + 4 = 0, t1 = 1, t2 = 4.
Очевидно, что разность синуса и косинуса не может равняться четырем, поскольку эти функции не принимают значений, модуль которых превышает 1; поэтому второй корень квадратного уравнения — посторонний. Для t = 1 сделаем обратную замену: sin x - cos x = 1. Применим метод дополнительного угла:
Пример 7.27.
Решение
Кроме того, 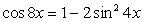 . Эти преобразования позволяют сделать замену:
. Эти преобразования позволяют сделать замену:
t = sin 4x и получить для t уравнение:
Сделаем обратную замену:
Комментарий. Данный пример предполагает использование тождеств: 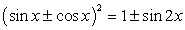
Комментарий. Решение следующих четырех примеров основано на формулах понижения степени. Напомним, что четные степени синуса и косинуса можно понизить переходом к двойному углу с помощью следующих формул:
Пример 7.28.
Решение
Понизим степени тригонометрических функций, входящих в уравнение:
Пример 7.29.
Решение
При понижении степени первого слагаемого оно выразится через cos 8x, поэтому у второго слагаемого мы не будем понижать степень, а вместо этого применим к нему основное тождество:
Пример 7.30.
Решение
Преобразуем разность четвертых степеней: cos 4x = sin x и применим формулу приведения:
Пример 7.31.
Решение
Пример 7.32.
Решение
Понизим степень в левой части уравнения, а в правой преобразуем произведение в сумму:
Пример 7.33.
Решить уравнение: 20tg 8x + 15sin 8x + 2tg 4x = 0.
Решение
Используем универсальную подстановку:
Случай 2: 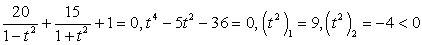 — постороннее решение.
— постороннее решение.
Пример 7.34.
Решение
Обратим внимание на то, что левую часть уравнения с помощью одной из формул универсальной подстановки можно представить как:
Обратная замена:
Комментарий. Уравнения, содержащие комбинации 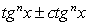 удобно решать, переходя к синусам и косинусам.
удобно решать, переходя к синусам и косинусам.
Пример 7.35.
Решить уравнение: 8sin 2x + 3 (tg x + ctg x) - 16 = 0.
Решение
Преобразуем сумму тангенса и котангенса:
Теперь можно сделать замену:
Обратная замена:
Пример 7.36.
Решение
Вновь выразим левую часть равенства через функции двойного угла:
Теперь уравнение принимает вид:
Комментарий. При решении тригонометрических уравнений (группа С) используются те же приемы, что и при решении алгебраических иррациональных уравнений. Особое внимание требуется обращать на дополнительные ограничения на допустимые значения неизвестного (самая распространенная ошибка в задачах этого типа — включение в ответ посторонних корней).
Пример 7.37.
Решение
ОДЗ задается неравенством: 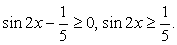 Возведем обе части в квадрат:
Возведем обе части в квадрат:
Обратная замена:
Пример 7.38.
Решение
Обратим внимание на то, что подкоренное выражение представляет собой полный квадрат: 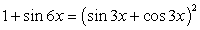 , следовательно,
, следовательно, 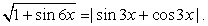
Сделаем замену: t = sin 3x + cos 3x, тогда | t | = 3 - 2t.
Случай 2: 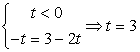 — посторонний корень (не соответствует условию раскрытия модуля).
— посторонний корень (не соответствует условию раскрытия модуля).
Пример 7.39.
Решение
Ограничение на ОДЗ: 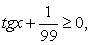 то есть
то есть 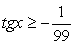 . Учитывая это условие, приравняем каждый множитель к нулю.
. Учитывая это условие, приравняем каждый множитель к нулю.
Следовательно, 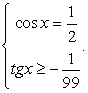 Этим условиям удовлетворяют углы вида
Этим условиям удовлетворяют углы вида 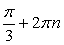 (вторая группа решений тригонометрического уравнения
(вторая группа решений тригонометрического уравнения 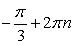 определяет углы, лежащие в четвертой четверти, тангенс которых равен
определяет углы, лежащие в четвертой четверти, тангенс которых равен 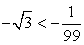 ).
).
Комментарий. Для решения тригонометрических уравнений с модулями применяются те же приемы, что и для алгебраических уравнений с модулями.
Пример 7.40.
Решить уравнение: sin 3x + | sin x | = 0.
Решение
Пример 7.41.
Решить уравнение: | sin 12x | + | sin 18x | = 0.
Решение
Сумма модулей может равняться нулю только в том случае, если при одном и том же значении х оба подмодульных выражения равны нулю. Следовательно, нужно найти общие корни двух уравнений: 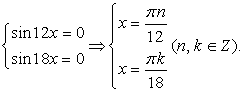
Принципиально важно то, что в решениях указаны разные целочисленные параметры. Для общих корней должно выполняться равенство 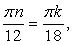 откуда
откуда 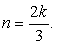
Поскольку n — целое число, дробь 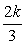 должна быть сократимой, а это возможно только если k кратно трем, то есть
должна быть сократимой, а это возможно только если k кратно трем, то есть 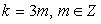 . Тогда решение уравнения можно записать так:
. Тогда решение уравнения можно записать так:
Комментарий. Рассмотрим далее тригонометрические уравнения с конечным числом корней. Эти уравнения очень необычны, и конечное число решений связано с тем, что аргумент тригонометрической функции принимает значения из некоторого конечного промежутка.
Пример 7.42.
Решение
Найдем множество значений функции 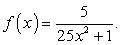 Очевидно, что
Очевидно, что 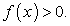 Исследуем ее на экстремум.
Исследуем ее на экстремум.
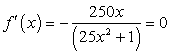 при х = 0 — найдена критическая точка.
при х = 0 — найдена критическая точка.
Слева от нее 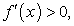 справа
справа 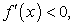 то есть это точка максимума. Так как он является единственным экстремумом, то при х = 0 функция принимает свое наибольшее значение: f (0) = 5.
то есть это точка максимума. Так как он является единственным экстремумом, то при х = 0 функция принимает свое наибольшее значение: f (0) = 5.
Решим простейшее тригонометрическое уравнение: 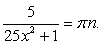 Из предыдущего исследования получаем, что равенство возможно только при условии
Из предыдущего исследования получаем, что равенство возможно только при условии 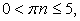 откуда
откуда 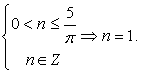
Действительно, это единственное целочисленное решение такого неравенства. Тогда 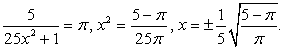
Комментарий. В следующем примере рассмотрим комбинированные задачи, в которых применяются известные из алгебры методы решения систем и способы решения тригонометрических уравнений. Важно помнить, что при решении системы ответ каждого простейшего уравнения должен записываться с новым целочисленным параметром, который может принимать любое возможное значение независимо от ранее введенных параметров.
Пример 7.43.
Решение
Применим метод алгебраического сложения: перейдем к системе, уравнениями которой будут сумма и разность исходных уравнений.
Вновь сложим и вычтем полученные уравнения:
Пример 7.44.
Решение
Используем подстановку из второго уравнения: 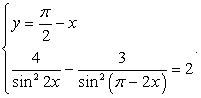 .
.
Применим формулу приведения:
Пример 7.45.
Решение
Вычтем первое уравнение из второго и применим формулу 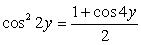
Случай 1: cos 4y = 1, тогда из второго уравнения 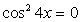 , то есть cos 4x = 0. Получена система двух простейших уравнений:
, то есть cos 4x = 0. Получена система двух простейших уравнений:
Решая полученную систему простейших уравнений, находим вторую группу корней:
Еще раз напомним, что решение каждого уравнения системы содержит свой целочисленный параметр (решением будет каждая пара чисел, заданная полученными формулами, в которых мы можем задавать n и k любые целые значения, не обязательно одинаковые).
Комментарий. Решением тригонометрического неравенства обычно является набор промежутков, границы которых можно задать общей формулой с использованием целочисленного параметра. Для определения границ очень удобно применять тригонометрическую окружность.
Пример 7.46.
Решение
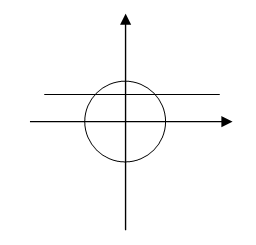
Решим сначала простейшее тригонометрическое неравенство 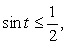 где
где 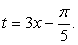
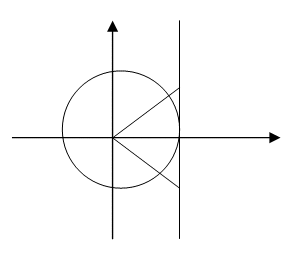
Прямая 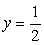 делит тригонометрическую окружность на две дуги. Решениям неравенства соответствуют точки на нижней дуге, ординаты которых не больше
делит тригонометрическую окружность на две дуги. Решениям неравенства соответствуют точки на нижней дуге, ординаты которых не больше 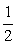 . Поэтому в пределах от
. Поэтому в пределах от 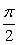 до
до 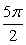 решение имеет вид:
решение имеет вид: 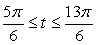 .
.
Границы следующего промежутка решений можно получить отсюда, изменив каждую границу на 2πn:
Сделав обратную замену, получим двойное неравенство для х:
Пример 7.47.
Решить неравенство: | tg x | ≥ 1.
Решение
Наименьший положительный период тангенса равен π, поэтому достаточно найти решение неравенства на интервале 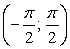 , а затем прибавить к границам πn. Раскрыв модуль, превратим неравенство в совокупность двух неравенств:
, а затем прибавить к границам πn. Раскрыв модуль, превратим неравенство в совокупность двух неравенств: 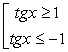 .
.
Дуги окружности, соответствующие их решениям, имеют вид:
Обращаем внимание на то, что точки 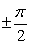 не входят в решение, поскольку при этих значениях аргумента тангенс не существует. Учитывая периодичность, находим окончательное решение:
не входят в решение, поскольку при этих значениях аргумента тангенс не существует. Учитывая периодичность, находим окончательное решение:
Комментарий. В более сложных неравенствах для их сведения к простейшим применяются в основном те же приемы, что и при решении уравнений.
Пример 7.48.
Решение
Представим cos 2x = 1 - 2sin2 x и сделаем замену: t = sin x. Тогда для t требуется решить систему неравенств:
Обратная замена приводит к уравнению sin x = -1, откуда 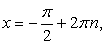 и неравенству
и неравенству 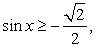 решение которого:
решение которого:
Пример 7.49.
Решение
Используем то, что 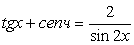 и сделаем замену: t = sin 2x. Неравенство для t имеет вид:
и сделаем замену: t = sin 2x. Неравенство для t имеет вид:
Методом интервалов находим решение:
Проводим обратную замену и решаем полученные тригонометрические неравенства:
Ответом будет объединение полученных промежутков.
Пример 7.50.
Решение
Преобразуем обе части неравенства.
Сделаем замену:
Следовательно, | tg 2x | ≥ 1, откуда:
Пример 7.51.
Решение
Поскольку обе части неравенства неотрицательны, можно возвести их в квадрат:
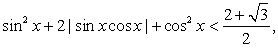 или
или 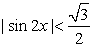 . Еще раз возведем обе части в квадрат:
. Еще раз возведем обе части в квадрат:
Получено простейшее тригонометрическое неравенство, решение которого:
 ;
;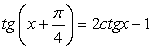 .
.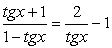 .
.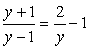 .
.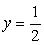 , т.е.
, т.е. 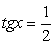 и
и 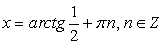 .
.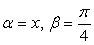 и
и 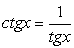 ).
).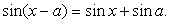
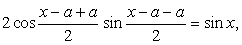 т.е.
т.е. 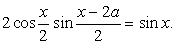
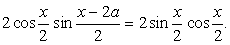
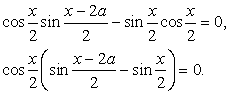
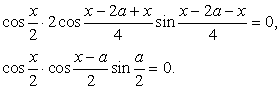
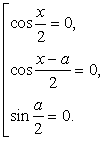

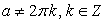 , то
, то 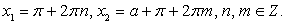
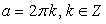 , то
, то 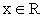 .
.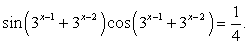
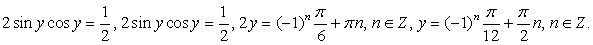
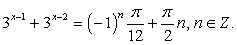
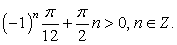
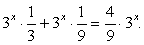
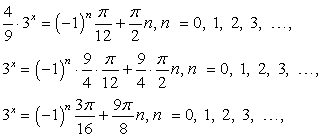
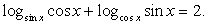
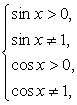 т.е. системой
т.е. системой 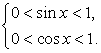
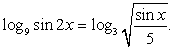
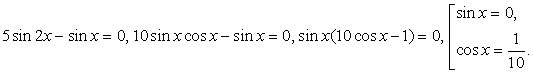
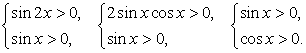
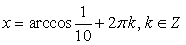 .
.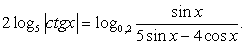
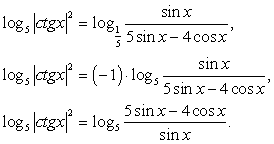
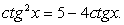
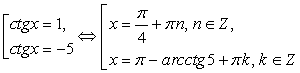 ,
,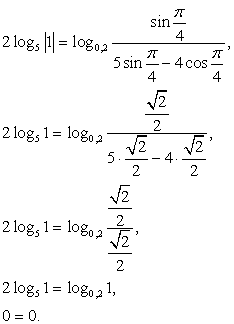
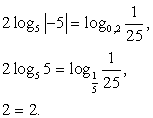
 .
. .
.
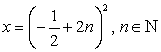 .
.
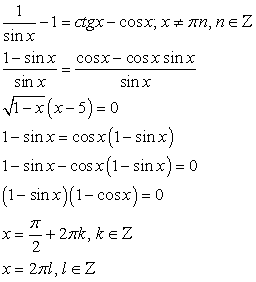
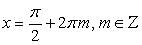 .
.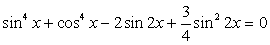 .
.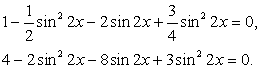
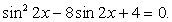
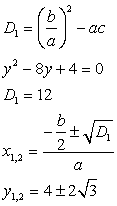
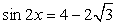 или
или
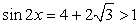
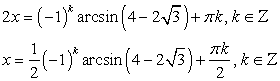
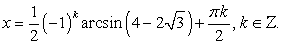
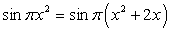 .
.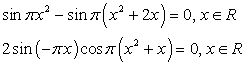
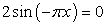 или
или 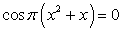
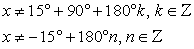
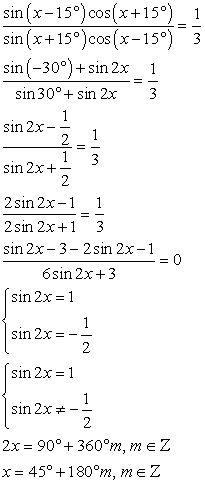
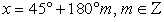 .
.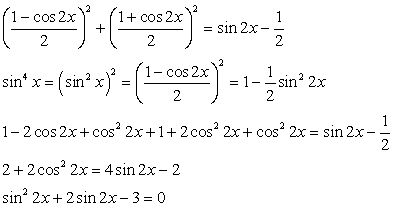
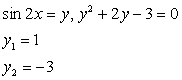
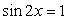 или
или 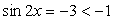
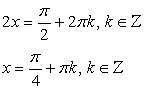
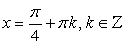 .
.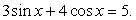
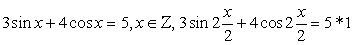 .
.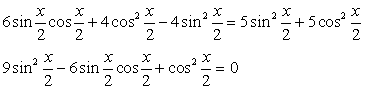
 .
.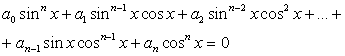 ,
,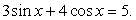
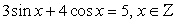
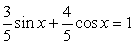 .
.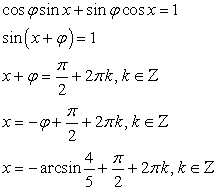
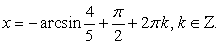
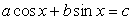 .
.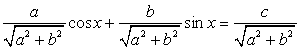 .
.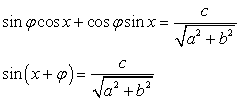
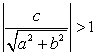 , т.е.
, т.е. 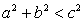 , то корней нет;
, то корней нет;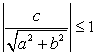 , т.е.
, т.е. 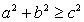 , тогда:
, тогда: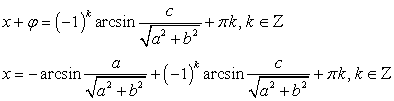
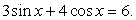
 .
.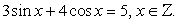
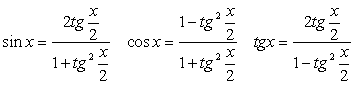
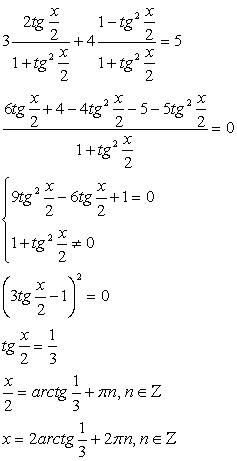
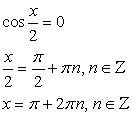
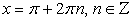 , тогда:
, тогда: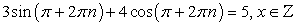 .
.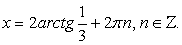
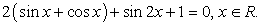
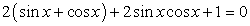 .
.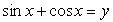 .
.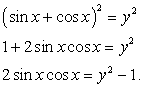
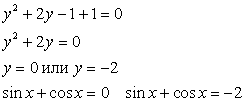
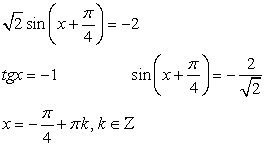
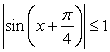 , при
, при 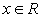 , то корней нет.
, то корней нет.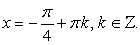
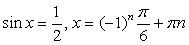 .
.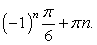
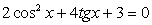 .
.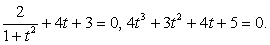
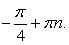
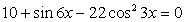
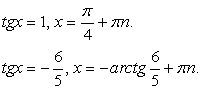
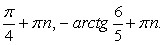
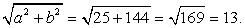
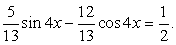
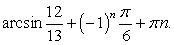
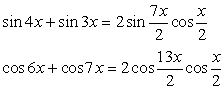 .
.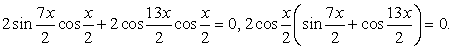
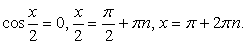
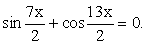
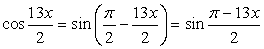 .
.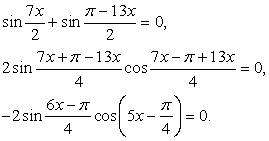
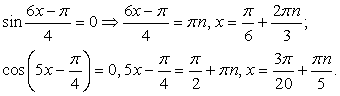
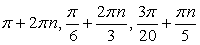 .
.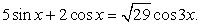
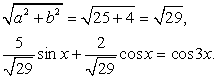
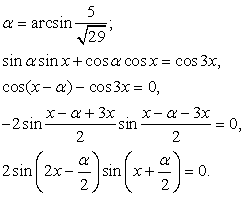
 .
.
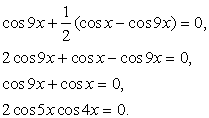
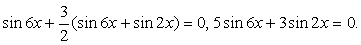
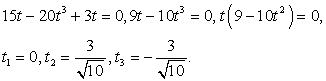
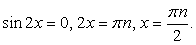
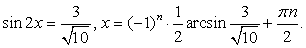
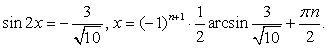
 .
.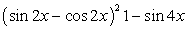 , представим
, представим 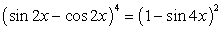 .
.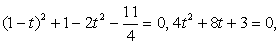
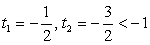 — посторонний корень.
— посторонний корень.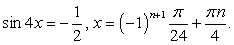
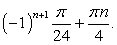
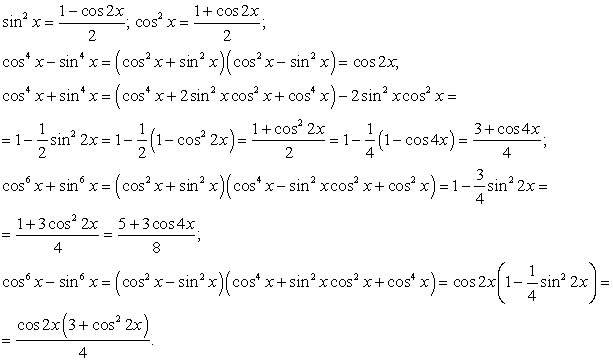
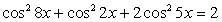
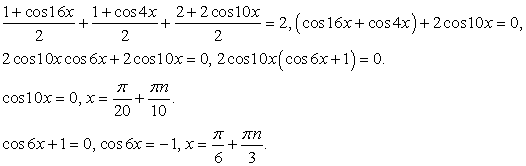
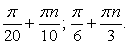
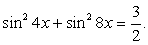
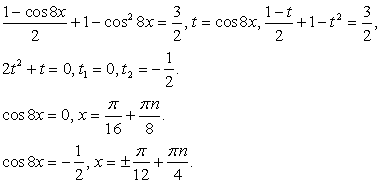
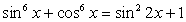
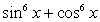 через
через 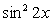 :
: 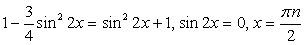 .
.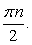
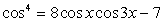
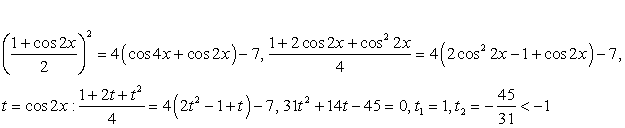 — посторонний корень.
— посторонний корень.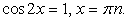
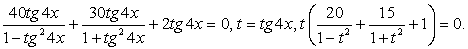
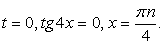
 — посторонний корень.
— посторонний корень.
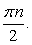
 — посторонний корень.
— посторонний корень.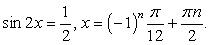
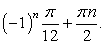
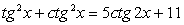
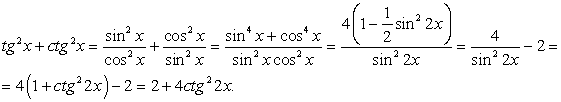
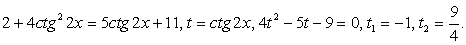
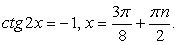
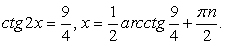
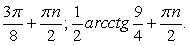
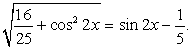
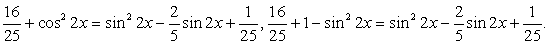
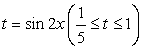 приводит к уравнению:
приводит к уравнению: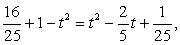
 — посторонний корень.
— посторонний корень.
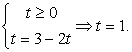
 .
. .
.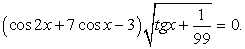
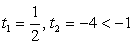 — посторонний корень.
— посторонний корень.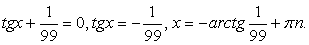
 .
.
 .
.
 .
.
 .
.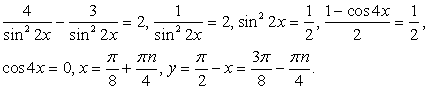
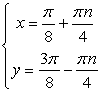 .
.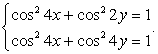
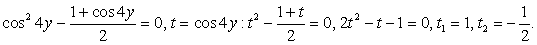
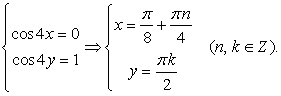
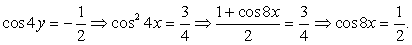
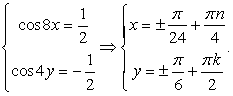
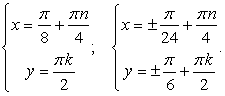
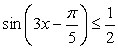 .
.
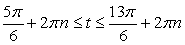 .
.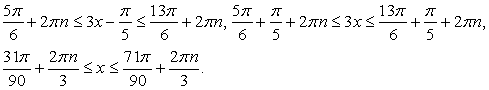
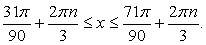
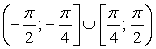 .
.
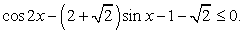
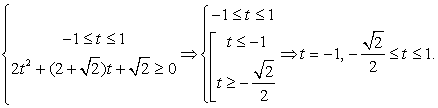
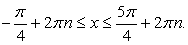
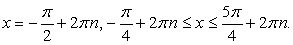
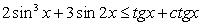
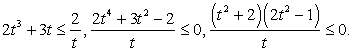
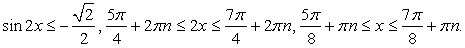
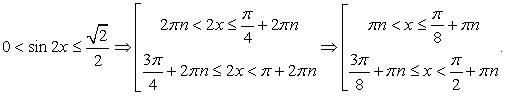
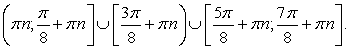
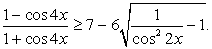
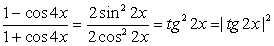 .
.