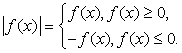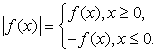Рациональные уравнения и неравенства в работах ЕГЭ часто «усложнены модулями». Уравнения и неравенства, содержащие переменную под знаком модуля, не входят явно в школьную программу по математике, часто предлагаются школьными учителями как задания повышенной сложности. В итоге, вызывая у абитуриентов страх и трепет, такие задания многими абитуриентами просто пропускаются, хотя вполне могли быть выполнены. Для этого необходимо не так много:

1) четко знать определение модуля;

2) понимать суть приема решения уравнений и неравенств, основанного на одновременном раскрытии всех модулей (причем, здесь достаточно конкретных примеров);

3) помнить о методе введения новой переменной.

Решение уравнений и неравенств, содержащих переменную под знаком модуля, основано на определении модуля:

Модули, входящие в уравнение или неравенство раскрываются по определению и в дальнейшем уже решаются уравнения и неравенства, не содержащие модуля. Заметим, что абитуриенты часто вместо равенства, указанного выше, применяют равенство:

Понятно, что оно справедливо лишь в случае f(x) = x. В общем случае это равенство неверно. Следует помнить об этом и не допускать этой распространенной среди абитуриентов ошибки.

Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.

Основной прием решения модульных уравнений и неравенств — раскрытие модуля с использованием его определения (| a | = a при a ≥ 0 и | a | = -a при a < 0). Для этого обычно рассматривают отдельно два случая: случай, когда подмодульное выражение неотрицательно и когда оно отрицательно.