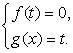Часто трудности с решением рациональных уравнений обусловлены для абитуриентов тем, что решение, как говорится «в лоб», по алгоритму метода разложения на множители:

,

где A (x), B (x) — произвольные рациональные выражения;

P (x), Q (x) — многочлены,

приводит к громоздким, «рутинным» преобразованиям или к необходимости находить корни многочленов степени большей, чем второй. А это уже не совсем «школьная» задача. При этом даже в самых очевидных случаях, абитуриенты не применяют метод введения новой переменной. А ведь, введение новой переменной позволяет быстро упростить решаемое уравнение. Это мощный метод, его следует понимать и применять.

Введение новой переменной осуществляется тогда, когда решаемое уравнение представимо в виде f (g (x)) = 0. Полагая g (x) = t, мы переходим к решению системы:

Если уравнения f (t) = 0, g(x) = t₁ , g(x) = t₂ ,…, g (x) = t_n , где t₁ , t₂ ,…, t_n  — корни уравнения f (t) = 0 проще исходного уравнения, то метод, как говорится, сработал.

Рассмотрим различные рациональные уравнения, для решения которых весьма полезен метод введения новой переменной, но не очевидны случаи, когда исходное уравнение непосредственно имеет вид f (g(x)) = 0. Поиск удачной подстановки g (x) = t и специальная работа по приведению исходного уравнения к указанному виду, составляет главную сущностную часть решения уравнения. Решение же уравнения f (t) = 0 и совокупности уравнений g (x) = t_i  — сравнительно несложная, техническая часть процесса решения уравнения.

Решение дробно-рациональных уравнений нередко сводится к решению обычных квадратных уравнений, но с учетом ограничений на допустимые значения неизвестного. В частности, из ОДЗ исключаются те значения х, при которых хотя бы один из знаменателей дробей, входящих в уравнение, обращается в 0.

Этапы решения рационального уравнения.

1. Определить ОДЗ (ни один знаменатель не может равняться нулю).

2. Найти наименьший общий знаменатель всех дробей.

3. Умножить уравнение на этот знаменатель и решить полученное целое уравнение.

4. Включить в ответ только те корни, которые входят в ОДЗ.
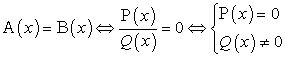