Комментарий. Цель данного раздела — проработать выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а так же комбинированных заданий. Для решения задач на упрощение тригонометрических выражений требуется достаточно хорошо знать правила преобразования алгебраических выражений и тригонометрические формулы (уметь применять их как по одной, так и в комплексе).
Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно.
Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы:
Формулы зависимости между функциями одного и того же аргумента:
1. |
|
4. |
|
2. |
|
5. |
|
3. |
|
6. |
|
Формулы сложения.
Формулы двойных и половинных углов.
1. |
5. | ||
2. |
6. | ||
3. |
7. | ||
4. |
8. |
Формулы преобразования суммы в произведение:
|
|
|
|
|
|
Формулы преобразования произведения в сумму:
Формулы приведения:
|
|
|
|
|
|
|
|
|
|
| sin φ | - sin α |
cos α |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos φ |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos α |
cos α |
tg φ |
- tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg φ |
- ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
Рассмотрим сначала достаточно простые задания на применение формул тригонометрии.
Пример 2.1.
Вычислить значение sin α, если cos α = 0,3, α — угол в первой четверти.
Решение
Применим основное тригонометрическое тождество, связывающее тригонометрические функции 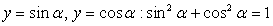 .
.
Так как по условию задачи cos α = 0,3, то cos2α
= 0,09. Значит, sin2α
+ 0,09 = 1, sin2α
= 1 – 0,09 = 0,91. Решая уравнение sin2α
= 0,91, получаем два случая (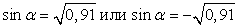 ), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно,
), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно, 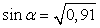 .
.
Пример 2.2.
Вычислите значение tg α, если ctg α = 0,2.
Решение
Воспользуемся формулой, связывающей тригонометрические функции y = tg α, y = ctg α : tg α ∙ ctg α = 1. Подставляя заданное в условии значение 0,2, получаем, что tg α ∙ 0,2 = 1, откуда tg α = 5.
Ответ:  5.
5.
Пример 2.3.
Упростите выражения;
Решение
Данные задания — на применение формул сложения.
1) 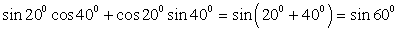 . Обратимся далее к таблице значений тригонометрических функций. Получаем, что
. Обратимся далее к таблице значений тригонометрических функций. Получаем, что 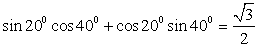 .
.
3) Воспользуемся формулой «косинус суммы», тогда 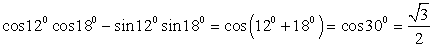 .
.
Пример 2.4.
Вычислите:
Решение
1) Воспользуемся свойством периодичности функции y = sin x, тогда 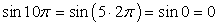 .
.
2) Так как период функции y = tg x равен π, получаем: 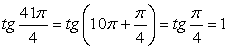 .
.
3) Представим 75° в виде суммы двух «удобных» слагаемых: 75° = 45° + 30°. Следовательно, 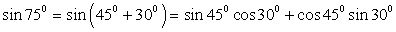 . Обратимся к табличным значениям тригонометрических функций, получим:
. Обратимся к табличным значениям тригонометрических функций, получим: 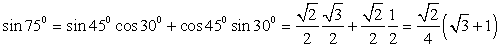 .
.
4) 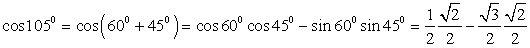 . Окончательно получаем, что
. Окончательно получаем, что 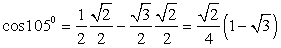 .
.
5) Для вычисления значения cos 15° представим 15° как 15° = 45° - 30° (или 15° = 60° - 45°). Тогда 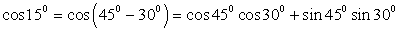 . Обратимся далее к табличным значениям тригонометрических функций. Получаем, что
. Обратимся далее к табличным значениям тригонометрических функций. Получаем, что 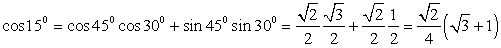 . Cледовательно,
. Cледовательно, 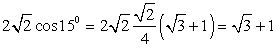 .
.
Отдельную группу заданий этого типа составляют задания на вычисление одних тригонометрических функций по известным другим.
Пример 2.5.
Известно, что sin α – cos α = 0,3. Найти:
1) sin2α ;
2) sin4α + cos4α ;
3) sin6α + cos6α .
Решение
1) Возведем в квадрат обе части заданного в условии примера равенства и используем формулу «квадрат разности», получаем, что:
sin2α - 2sinα cosα + cos2α = 0,09.
Вспомним основное тригонометрическое тождество и применим формулу синуса двойного угла:
1 - sin2α = 0,09, откуда:
sin2α = 1 - 0,09 = 0,91.
2) Воспользуемся полученным результатом для ответа на вопрос 2.
Для этого сумму sin4α + cos4α представим в специальном виде:
sin4α + cos4α = (sin4α + 2sin2α cos2α + cos4α ) — 2sin2α cos2α = (sin2α + cos2α )2 - 1/2 ∙ sin2 2α = 1 - 1/2 ∙ 0,91 = 0,545.
Комментарий. Специальный вид, использованный при решении данного примера, позволяет применить формулу «квадрат суммы» и использовать результат, полученный в пункте 1. При последующих преобразованиях использована формула синуса двойного угла.
3) Обратим внимание, что для вычисления значения выражение sin6α + cos6α можно представить в виде суммы кубов.
sin6α + cos6α = (sin2α )3 + (cos2α )3 = (sin2α + cos2α )(sin4α - sin2α cos2α + cos4α ) = 1 ∙ (0,545 – 1/4 ∙ 0,91) = 0,3175.
Ответ:

1) 0,91;
2) 0,545;
3) 0,3175.
Пример 2.6.
Решение
Проверкой можно убедиться, что при cos α = 0 приведенное равенство неверно. Поэтому следует разделить числитель и знаменатель дроби на cos α (на основании основного свойства дроби):
раскрывая скобки, приведем далее подобные слагаемые:
3tgα + 4 = 5tgα - 10, 2tgα = 14, получаем, что tgα = 7.
Ответ:  7.
7.
Пример 2.7.
Вычислить cos α, если cos2α = 3/4 и 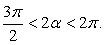
Решение
Как известно, 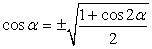 . Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим:
. Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим:
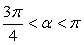 , то есть угол α располагается во второй четверти и, следовательно, cos α < 0.
, то есть угол α располагается во второй четверти и, следовательно, cos α < 0.
В приведенной выше формуле выберем знак «минус»:
Комментарий. Следующая группа заданий — вычисление значений различных тригонометрических выражений с использованием тригонометрических формул.
Пример 2.8.
Выполним упрощение каждой дроби по отдельности.
С целью сокращения дроби 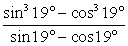 воспользуемся формулой «разность кубов» и получим:
воспользуемся формулой «разность кубов» и получим:
Рассмотрим далее выражение 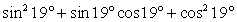 . Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом:
. Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом:
Обратимся далее к преобразованию второй дроби. Применим одну из формул приведения: 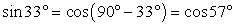 . Поэтому:
. Поэтому:
Ответ:  1.
1.
Пример 2.9.
Вычислить sin10° sin30° sin50° sin70°.
Используем формулу преобразования произведения тригонометрических функций в сумму: sin10° sin50° = 1/2 (cos40° - cos60°) = 1/2 cos 40° - 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30° = 1/2, получаем:
Комментарий. Для выполнения аналогичных заданий необходимо знание не только тригонометрических формул, но и табличных значений тригонометрических функций.
Рассмотрим далее примеры упрощения тригонометрических выражений с произвольным аргументом.
Пример 2.10.
Так как числитель заданной дроби имеем достаточно простой вид, начнем с упрощения знаменателя. Для этого применим представление 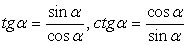 :
:
Приведем полученную разность дробей к общему знаменателю:
Пример 2.11.
Комментарий. Задания на доказательство тождеств вполне можно воспринимать как задания на упрощение выражений, причем с готовым ответом в виде более простой и компактной части равенства.
Решение
В частности, в данном примере попробуем упростить левую часть, чтобы получить такое же выражение, как справа. Для этого помножим числитель и знаменатель подкоренного выражения на 1 + sin α:
Исследуем далее знак числителя и знаменателя подмодульного выражения:
sin α ≥ -1, тогда 1 + sin α ≥ 0 поэтому 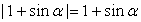 ;
;
Таким образом:
Аналогичным образом преобразуем второе слагаемое левой части:
что и требовалось доказать.
Пример 2.12.
Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если 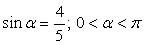 .
.
Решение
Выпишем формулы для вычисления искомых функций:
Из основного тригонометрического тождества вычислим:
Далее найдем значения искомых выражений:
Пример 2.13.
Решение
Приведем левую часть к 1:
Тождество доказано.
Пример 2.14.
Вычислить значение выражения:
Решение
Далее, используя формулы приведения, получим:
Воспользуемся табличными значениями и свойствами тригонометрических функций:
Итак, значение выражения равно 0.
Ответ:  0.
0.
Комментарий. Для выполнения заданий, связанных с обратными тригонометрическими функциями, нужно, во-первых, четко помнить определения этих понятий:
Удобно при решении таких задач сделать замену (например, α = arcsin x) и работать с более привычным объектом — углом α, лежащем в первой или четвертой четверти тригонометрического круга, синус которого равен х. При этом выясняется, что задача намного проще, чем казалось вначале.
Пример 2.15.
Вычислить cos(4arctg 5).
Решение
Пусть α = arctg5, тогда tg α = 5. Требуется найти cos4α. Вычислим вначале cos2α, используя универсальную подстановку:
Тогда получаем, что:
Пример 2.16.
Выразить через все обратные функции 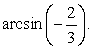
Решение
Пусть  . Угол α лежит в четвертой четверти, следовательно, cos α > 0.
. Угол α лежит в четвертой четверти, следовательно, cos α > 0.
Найдем все тригонометрические функции угла:
В четвертой четверти находятся арктангенсы отрицательных чисел, поэтому можно утверждать, что 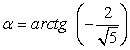 .
.
Но 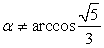 , так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом
, так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом 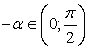 , то есть
, то есть 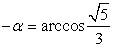 , тогда
, тогда 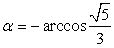 .
.
Арккотангенсы отрицательных чисел расположены во второй четверти. Например, 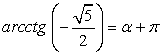 , следовательно,
, следовательно, 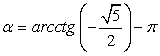 . Таким образом, угол α выражен через все обратные функции.
. Таким образом, угол α выражен через все обратные функции.
Пример 2.17.
Найти arcsin (sin 12).
Решение
По условию задачи требуется найти угол, синус которого равен синусу угла в 12 радиан и который принадлежит промежутку 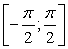 . Заметим, что
. Заметим, что 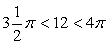 , поэтому
, поэтому 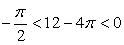 .
.
Поскольку 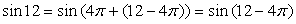 , угол 12 - 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
, угол 12 - 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
Ответ:  arcsin (sin12) = 12 - 4π.
arcsin (sin12) = 12 - 4π.
Пример 2.18.
Решение
Введем два угла: 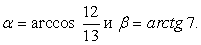 Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что
Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что 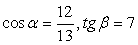 . Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
. Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
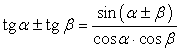
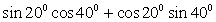 ;
;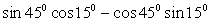 ;
;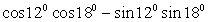 ;
;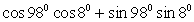 ;
;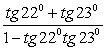 ;
;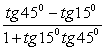 ;
;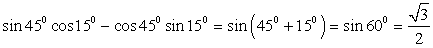 .
.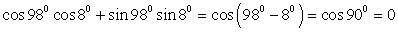 .
.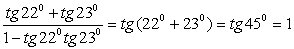 .
.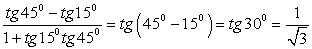 .
.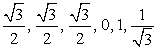
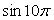 ;
;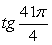 ;
;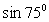 ;
;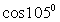 ;
;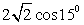 .
.
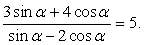
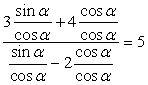 , следовательно,
, следовательно, 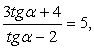 тогда:
тогда: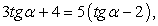
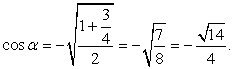
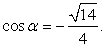
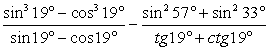 .
.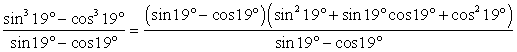 .
.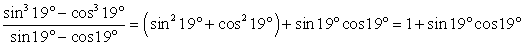 .
.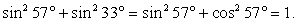
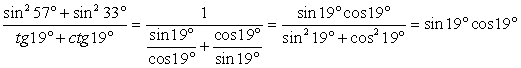 .
.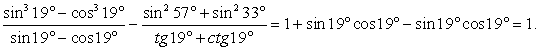
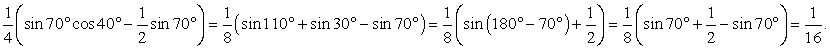
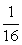
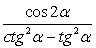 .
.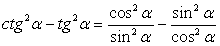 .
.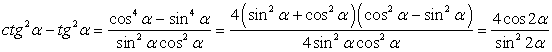 .
.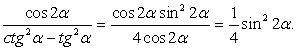
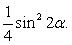
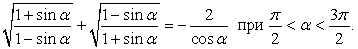
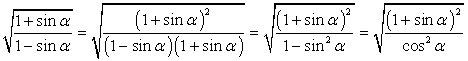 .
.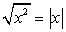 , получаем
, получаем 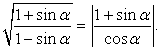
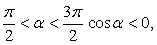 следовательно,
следовательно, 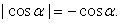
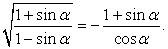
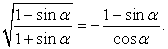
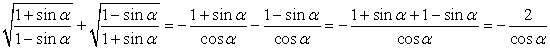
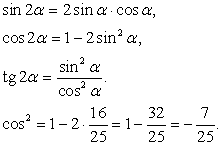 .
.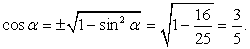
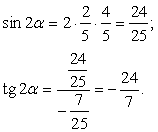
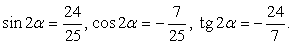
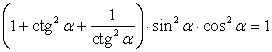 .
.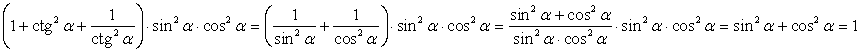 .
.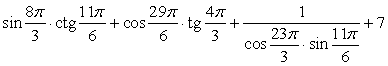 .
.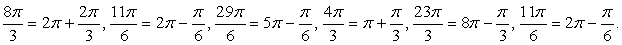
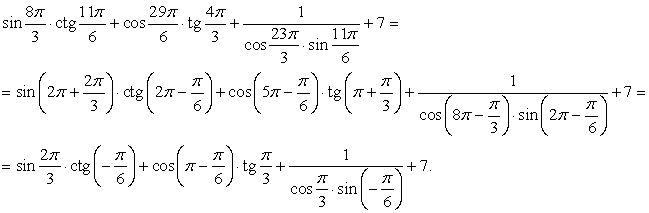
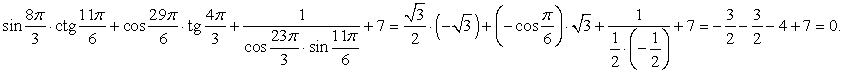
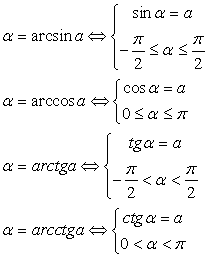
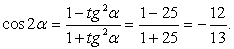
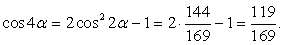
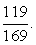
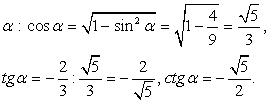
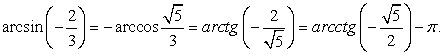
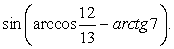
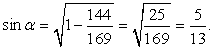
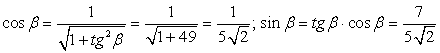 .
.